文字识别模型MNIST

目录

1 简介

2 数据集

3 设置神经元数量

4 设置正向传播函数

5 设置损失函数以及展示用参数

6 训练与展示

---

1 简介

MNIST是一个入门级的计算机视觉数据集，它包含各种从0到9的手写数字图片以及对应的标签，本篇使用了两层简单神经元来实现手写图片预测，主要目的在于熟悉Tensorflow的使用流程。

2 数据集

本篇使用MNIST数据集，首先导入包：

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data

然后获得数据集并查看数据格式：

print("Download and Extract MNIST dataset")
mnist = input_data.read_data_sets('data/', one_hot = True)
print
print(" type of 'mnist' is %s" % (type(mnist)))
print(" number of train data is %d" % (mnist.train.num_examples))
print(" number of test data is %d" % (mnist.test.num_examples))

 

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('data/', one_hot = True)

以上两条语句会下载好MNIST数据

集到代码同文件夹下的data文件夹中，若网络不好，可以直接百度MNIST的数据集，通过国内网站下载下来放入data文件夹中。

MNIST数据集包含4个文件：

• 训练数据：train-images-idx3-ubyte.gz

• 训练标签：train-labels-idx1-ubyte.gz

• 测试数据：t10k-images-idx3-ubyte.gz

• 测试标签：t10k-labels-idx1-ubyte.gz

其中训练数据共55000个，测试数据10000个，每一个MNIST数据单元都由两部分组成：一张手写数字图片与一个对应的标签（即图片对应的数字）；

每张手写图片包含28x28x1即784个像素点，标签为手写数字的结果。

我们可以查看一下数据集的实例：

print("How does the training data look like?")
nsample = 5
randidx = np.random.randint(trainimg.shape[0], size=nsample)
​
for i in randidx:
    curr_img   = np.reshape(trainimg[i, :], (28,28)) # 28 by 28 matrix
    curr_label = np.argmax(trainlabel[i, :] ) # Label
    plt.matshow(curr_img, cmap=plt.get_cmap('gray'))
    plt.title("" + str(i) + "th Training Data " 
              + "Label is " + str(curr_label))
    print("" + str(i) + "th Training Data " 
              + "Label is " + str(curr_label))
    plt.show()

 

3 设置神经元数量

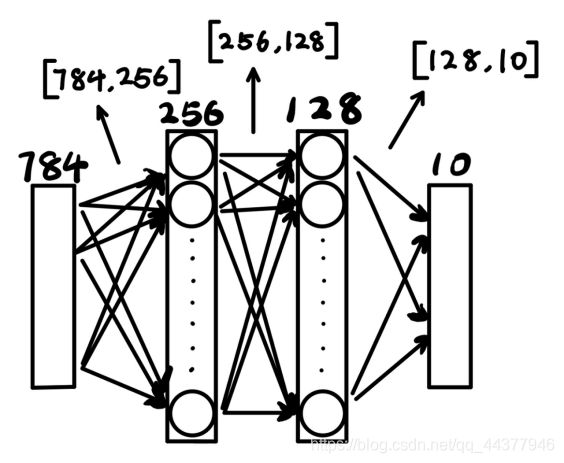
本次训练使用两层神经网络进行训练，第一层设置256个神经元，第二层设置128个神经元，输入为图片像素点数784，输出为预测的各数字的概率，即10；

故输入层与第一层神经元之间的权重w1为[784,256]，偏置b1为[256];

第一层神经元与第二层神经元之间的权重w2为[256,128]，偏置b2为[125];

第二层神经元与输出之间的权重out为[128,10]，偏置out为[10]。

各权重与偏置都为自动生成的随机值，设置标准差为0.1。

# 神经元个数
n_input    = 784
n_classes  = 10
n_hidden_1 = 256
n_hidden_2 = 128
​
#输入与输出
x = tf.placeholder("float", [None, n_input])    # None表示任意值，
y = tf.placeholder("float", [None, n_classes])  # 实际是后面指定的batch值
​
# 权重与偏置
stddev = 0.1
weights = {
    'w1': tf.Variable(tf.random_normal([n_input, n_hidden_1], stddev=stddev)),
    'w2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2], stddev=stddev)),
    'out': tf.Variable(tf.random_normal([n_hidden_2, n_classes], stddev=stddev)),
}
biases = {
    'b1': tf.Variable(tf.random_normal([n_hidden_1])),
    'b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'out': tf.Variable(tf.random_normal([n_classes])),
}
print("Network Ready")

4 设置正向传播函数

作矩阵乘法X · w ，然后加上偏置b，最后通过ReLU激活函数：

def multilayer_perception(_X, _weights, _biases):
    layer_1 = tf.nn.relu(tf.add(tf.matmul(_X, _weights['w1']),  _biases['b1'])) #y=x*w+b
    layer_2 = tf.nn.relu(tf.add(tf.matmul(layer_1, _weights['w2']), _biases['b2']))
    return(tf.add(tf.matmul(layer_2, _weights['out']), _biases['out']))

关于激活函数，因为对于矩阵乘法，A·B·C = A·(B·C)，无论设置多少层神经网络，对A来说都是只乘了一个矩阵，即最终效果相当于只有一层神经网络。因此每过一层神经网络，都需要过一次激活函数，进行一次非线性变换，如此才可使得多层神经网络真正起到效果。

5 设置损失函数以及展示用参数

为了调整权重使得预测的精度更高，需要设置适当的损失函数，使模型向着损失值减小的方向迭代。

这里采用了预测值与标签值之间的交叉熵作为损失函数，使用梯度下降算法以0.001的学习率使损失值最小化。

# 预测值
pred = multilayer_perception(x, weights, biases)
# 损失值
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
# 优化器
optm = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost)
# 中途展示用数据
corr = tf.equal(tf.argmax(pred,1), tf.argmax(y,1)) #0到9的概率，最大的为预测结果
accr = tf.reduce_mean(tf.cast(corr, "float"))  #平均精度
​
print("Functions Ready")

通过验证预测结果与标签是否一致，判断此次预测是否成功，将多次验证的成功率作为展示用的平均精度。

6 训练与展示

设置批处理个数 batch_size 为100，每次读入100个MNIST数据，设置迭代轮数 training_epochs 为20，总计进行20轮数据集的迭代，每进行4轮展示一次当前模型的预测效果。

此处批处理的数据读入使用了数据集提供的 mnist.train.next_batch(batch_size)

training_epochs = 20
batch_size      = 100
display_step    = 4
​
# 初始化
init = tf.global_variables_initializer()
​
sess = tf.Session()
sess.run(init)
​
for epoch in range(training_epochs):
    avg_cost = 0.
    total_batch = int(mnist.train.num_examples/batch_size)
    
    for i in range(total_batch):
        batch_xs, batch_ys = mnist.train.next_batch(batch_size) #如果是自己数据集，需要自己写函数
        feeds = {x: batch_xs, y: batch_ys}
        sess.run(optm, feed_dict=feeds)
        avg_cost += sess.run(cost, feed_dict=feeds)
    avg_cost /= total_batch
    
    # 展示
    if(epoch+1) % display_step == 0:
        print("Epoch: %03d/%03d cost: %.9f" %(epoch, training_epochs, avg_cost))
        #训练样本的精度
        feeds = {x: batch_xs, y: batch_ys}
        train_acc = sess.run(accr, feed_dict=feeds)
        print("Train Accuracy: %.3f" % (train_acc))
        #测试集的精度
        feeds = {x: mnist.test.images, y: mnist.test.labels}
        test_acc = sess.run(accr, feed_dict=feeds)
        print("Test Accuracy: %.3f" % (test_acc))
​
print("Optimization Finished")

得到训练结果：

最后得到的预测准确率在90%左右，因本次训练采用的模型比较简单，所以准确率不高，若想继续提高准确率，可以采用其他一些比较经典的神经网络模型。