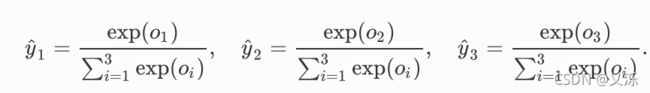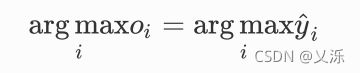Softmax回归模型及其代码实现
一、Softamx回归模型的原理
softmax回归跟线性回归一样,都是将输入特征与权重做线性叠加。与线性回归的一个主要不同在于,softmax回归的输出值个数等于标签里的类别数。比如线性回归中很常见的问题----预测房屋价格,我们通常会选取面积(平方米)和房龄(年)作为影响价格的两个因素,在这里面积和房龄作为特征而输出只有一个价格的预测值。而对于softmax,它更适用于做分类预测,比如在垃圾邮件分类问题中,我们往往需要选取几个主要的特征作为系统的输入,然后经过softmax分类算法得到邮件是垃圾邮件、不是垃圾邮件的概率值,它的输出是离散的值。
现在我们具体看一下softmax模型是怎样得到的。假如我们需要对三类动物(狗、猫、鸡)进行分类,我们选取动物的四个特征作为输入,这时一共有4种特征和3种输出动物类别,所以权重包含12个标量(带下标的w)、偏差包含3个标量(带下标的b),且对每个输入计算o1,o2,o3这三个输出:
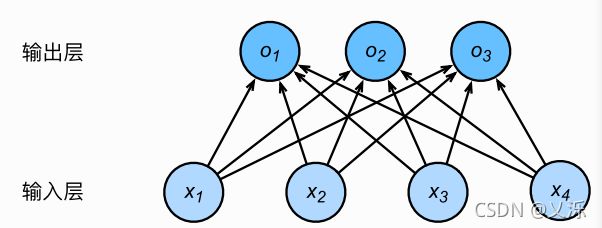
图1.1用神经网络图描绘了上面的计算。 softmax回归同线性回归一样,也是一个单层神经网络。由于每个输出O1,O2,O3的计算都要依赖于所有的输入x1,x2,x3,x4,softmax回归的输出层也是一个全连接层。
图1.1 softmax回归是一个全连接层
既然分类问题需要得到离散的预测输出,一个简单的办法是将输出值Oi当作预测类别是i的置信度,并将值最大的输出所对应的类作为模型的预测输出,即找到argmaxOi。例如,如果O1,O2,O3分别为0.1,10,0.1,由于O2最大,那么预测类别为2,为猫。
然而,直接使⽤用输出层的输出有两个问题。一方面,由于输出层的输出值的范围不确定,我们难以直观上判断这些值的意义。例如,刚才举的例子中的输出值10表示“很置信”图像类别为猫,因为该输出值是其他两类的输出值的100倍。但如果O1 = O3 = 10*3 ,那么输出值10却又表示图像类别为猫的概率很低。另一方面,由于真实标签是离散值,这些离散值与不确定范围的输出值之间的误差难以衡量。
softmax运算符(softmax operator)解决了以上两个问题。它通过下式将输出值变换成值为正且和为1的概率分布:
其中
因此,我们便得到了一个合法的概率分布这时候我们便可以直接通过输出y_hat(y帽)的值进而预测的类别。
因此softmax运算不不改变预测类别输出。
二、Softmax回归的简单实现
我们已经简单了解了softmax回归模型的原理,接下来,让我们一起用pytorch来实现一个softmax回归模型。首先导入所需的包和模块。
import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l注:1.d2lzh_pytorch是需要自己去下载的,通过它可以直接调用写好的函数,方便编写程序。安装d2lzh_pytorch 包 - 简书 (jianshu.com)
2.torch.nn仅支持输入一个batch的样本不支持单个样本输入,如果只有单个样本可用input.unsqueeze(0)来添加一维。
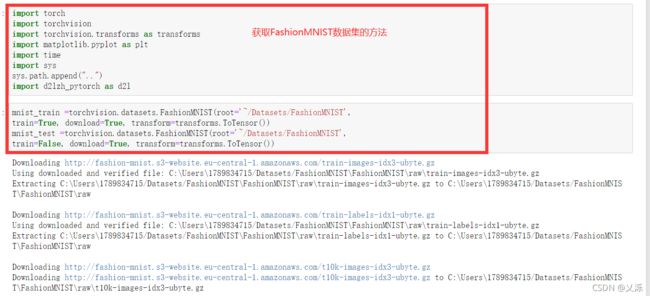
获取和读取数据。代码使用了Fashion-MNIST数据集,,设置每次读取的批量大小。
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)softmax回归的输出层是一个全连接层,所以我们用一个线性模块就可以了。因选取的每个batch样本x的形状为(batch_size,1,28,28),所以用view()将x的形状转换成(batch_size,784)后,再送入全连接层。
num_inputs = 784
num_outputs = 10
class LinearNet(nn.Module):
def __init__(self, num_inputs, num_outputs):
super(LinearNet, self).__init__()
self.linear = nn.Linear(num_inputs, num_outputs)
def forward(self, x): # x shape: (batch, 1, 28, 28)
y = self.linear(x.view(x.shape[0], -1))
return y
net = LinearNet(num_inputs, num_outputs)我们将x形状转化的功能函数自定义一个FlattenLayer并记录在d2llzh_pytorch中方便后面使用。
class FlattenLayer(nn.Module):
def __init__(self):
super(FlattenLayer, self).__init__()
def forward(self, x): # x shape: (batch, *, *, ...)
return x.view(x.shape[0], -1)这样我们就可以更更⽅方便便地定义我们的模型:
from collections import OrderedDict
net = nn.Sequential(
# FlattenLayer(),
# nn.Linear(num_inputs, num_outputs)
OrderedDict([
('flatten', FlattenLayer()),
('linear', nn.Linear(num_inputs, num_outputs))])
)然后,我们使⽤用均值为0、标准差为0.01的正态分布随机初始化模型的权重参数。
init.normal_(net.linear.weight, mean=0, std=0.01)
init.constant_(net.linear.bias, val=0)PyTorch提供了了一个包括softmax运算和交叉熵损失计算的函数。它的数值稳定性更好。
loss = nn.CrossEntropyLoss()我们使⽤用学习率为0.1的小批量量随机梯度下降作为优化算法。
optimizer = torch.optim.SGD(net.parameters(), lr=0.1)接下来,我们使用训练函数来训练模型。
def train_ch3(net, train_iter, test_iter, loss, num_epochs,batch_size,params=None, lr=None,optimizer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y).sum()
# 梯度清零
if optimizer is not None:
optimizer.zero_grad()
elif params is not None and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
if optimizer is None:
d2l.sgd(params, lr, batch_size)
else:
optimizer.step() # “softmax回归的简洁实现”⼀一节将⽤用到
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) ==y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'% (epoch + 1,
train_l_sum / n, train_acc_sum / n,test_acc))num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs,
batch_size, None, None, optimizer)输出:
poch 1, loss 0.0031, train acc 0.745, test acc 0.790
epoch 2, loss 0.0022, train acc 0.812, test acc 0.807
epoch 3, loss 0.0021, train acc 0.825, test acc 0.806
epoch 4, loss 0.0020, train acc 0.832, test acc 0.810
epoch 5, loss 0.0019, train acc 0.838, test acc 0.823参考: Dive-into-DL-PyTorch