BERT模型—6.对抗训练原理与代码实现

引言

  对抗训练对于NLP来说，是一种非常好的上分利器，所以，非常有必要加深对对抗训练的认识。

一、对抗训练一般原理

  小学语文课上，我们都学习过《矛与盾》这篇课文，

从辩证唯物史观角度来看，矛与盾并没有严格意义上的谁更厉害，谁一直占优。矛盾着的双方又同一又斗争，双方力量此长彼消，不断前进，从而推动事物发展。这也就是对抗训练。

1.对抗样本

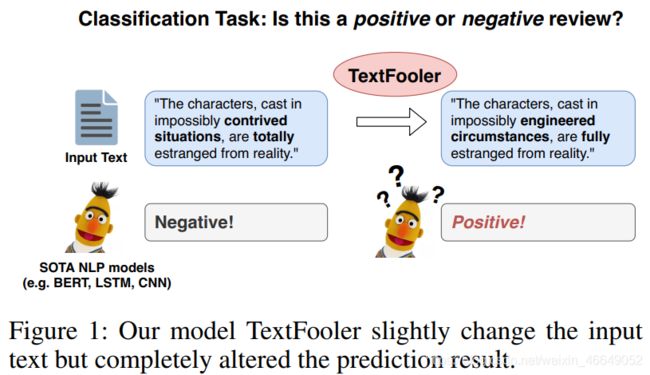
  两句话，只是部分英文单词发生了改变，但是在我们看来，含义还是几乎不变的，但是就是这种变化，基于BERT的文本分类模型对句子的情感分类居然是完全相反的。

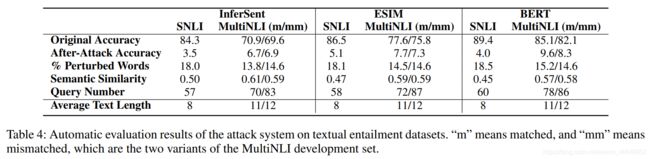
  根据研究，我们发现InferSent MultiNLI模型、ESIM MultiNLI模型、BERT MultiNLI模型在SNLI数据集上面准确率为84%以上，但是在对抗文本上，不管是传统的深度网络还是BERT模型，准确率都只有个位数。尽管BERT模型经过微调可以在不同的下游任务得到好的结果，但仍然是非常容易受到攻击的（模型不鲁棒）。

  那么，如何使得模型更加鲁棒呢？比如：

• 我们可以对数据进行处理，将对攻击的防御放到数据处理过程中
• 我们也可以对模型输出的向量表征做一些转换，将防御放在模型的输出端
• 我们也可以将防守放在模型本身上来

二、对抗训练的经典算法

  lan Goodfellow提出对抗训练方法，它的思想是在训练时，在原始的输入样本中加上扰动（对抗样本），我们用对抗样本来进行模型的训练，使得模型更加鲁棒

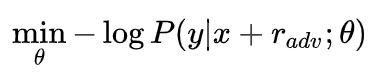
扰动的计算方式定义为：求得模型损失，对于$x$求梯度，对所求的梯度经过符号函数处理，在乘以一个系数$ϵ$

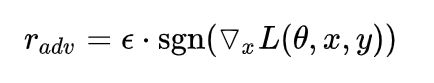
这种对抗训练的方法叫做Fast Gradient Sign Method (FGSM)。
  对抗训练其实可以当做正则化，减少模型的过拟合，提升模型的泛化性能。FGSM对抗训练方法应用与CV，cv的输入都是图像，图像输入模型时为RGB三个通道上的像素值，它的输入本身就是连续的，但是NLP的输入是离散的单词序列。那么，我们应该如何在NLP模型上定义对抗训练？
  虽然NLP的输入都是离散的单词序列，但是会经过embedding转变成低维空间上的向量表征，我们可以将embedding后的向量表征当成上述对抗训练模型中的$x$。lan Goodfellow在2017年提出了在连续的embedding上做扰动。

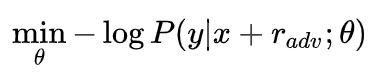
扰动的计算方式为：

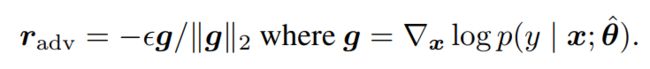
• $x$表示文本序列的embedding vectors

这种对抗训练的方法叫做Fast Gradient Method (FGM)。FGM通过一步，就移动到对抗样本上，如果梯度太大，可能会导致扰动过大,对模型造成误导。
  FGM对抗训练方法一步得到对抗样本，容易导致扰动过大。Projected Gradient Descent
(PGD)方法限定了扰动的范围，对抗样本并不是一步就得到了，而是通过沿着不同点的梯度走了多步之后再去得到。

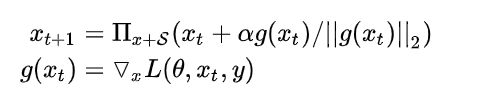
其中，

• 小步走:如果沿着梯度走的比较远，则通过投影的方式，投影到球面s上；
• 多步走:生成一个对抗样本是走多步得到的；

这种对抗训练的方法叫做Projected Gradient Descent(PGD)。

三、对抗训练代码实现

1.FGM

class FGM():
    """
    定义对抗训练方法FGM,对模型embedding参数进行扰动
    """
    def __init__(self, model, epsilon=0.25,):
        # BERT模型
        self.model = model
        # 求干扰时的系数值
        self.epsilon = epsilon

        self.backup = {}

    def attack(self, emb_name='word_embeddings'):
        """
        得到对抗样本
        :param emb_name:模型中embedding的参数名
        :return:
        """
        # 循环遍历模型所有参数
        for name, param in self.model.named_parameters():
            # 如果当前参数在计算中保留了对应的梯度信息，并且包含了模型中embedding的参数名
            if param.requires_grad and emb_name in name:
                # 把真实参数保存起来
                self.backup[name] = param.data.clone()
                # 对参数的梯度求范数
                norm = torch.norm(param.grad)
                # 如果范数不等于0并且norm中没有缺失值
                if norm != 0 and not torch.isnan(norm):
                    # 计算扰动，param.grad / norm=单位向量，起到了sgn(param.grad)一样的作用
                    r_at = self.epsilon * param.grad / norm
                    # 在原参数的基础上添加扰动
                    param.data.add_(r_at)

    def restore(self, emb_name='word_embeddings'):
        """
        将模型原本的参数复原
        :param emb_name:模型中embedding的参数名
        """
        # 循环遍历模型所有参数
        for name, param in self.model.named_parameters():
            # 如果当前参数在计算中保留了对应的梯度信息，并且包含了模型中embedding的参数名
            if param.requires_grad and emb_name in name:
                # 断言
                assert name in self.backup
                # 取出模型真实参数
                param.data = self.backup[name]
        # 清空self.backup
        self.backup = {}

# 实例初始化
fgm = FGM(model)
for batch_input, batch_label in data:
    # 正常训练
    loss = model(batch_input, batch_label)
    # 反向传播，得到正常的grad
    loss.backward() 
    # 对抗训练，在embedding上添加对抗扰动
    fgm.attack() 
    # embedding参数被修改，此时，输入序列得到的embedding表征不一样                     
    loss_adv = model(batch_input, batch_label)
    # 反向传播，并在正常的grad基础上，累加对抗训练的梯度
    loss_adv.backward() 
    # 恢复embedding参数
    fgm.restore() 
    # 梯度下降，更新参数
    optimizer.step()
    # 将梯度清零
    model.zero_grad()

2.PGD

class PGD():
    """
    定义对抗训练方法PGD
    """
    def __init__(self, model, epsilon=1.0, alpha=0.3):
        # BERT模型
        self.model = model
        # 两个计算参数
        self.epsilon = epsilon
        self.alpha = alpha
        # 用于存储embedding参数
        self.emb_backup = {}
        # 用于存储梯度，与多步走相关
        self.grad_backup = {}

    def attack(self, emb_name='word_embeddings', is_first_attack=False):
        """
        对抗
        :param emb_name: 模型中embedding的参数名
        :param is_first_attack: 是否是第一次攻击
        """
        # 循环遍历模型的每一个参数
        for name, param in self.model.named_parameters():
            # 如果当前参数在计算中保留了对应的梯度信息，并且包含了模型中embedding的参数名
            if param.requires_grad and emb_name in name:
                # 如果是第一次攻击
                if is_first_attack:
                    # 存储embedding参数
                    self.emb_backup[name] = param.data.clone()
                # 求梯度的范数
                norm = torch.norm(param.grad)
                # 如果范数不等于0
                if norm != 0:
                    # 计算扰动,param.grad / norm=单位向量相当于sgn符号函数
                    r_at = self.alpha * param.grad / norm
                    # 在原参数的基础上添加扰动
                    param.data.add_(r_at)
                    # 控制扰动后的模型参数值
                    # 投影到以原参数为原点，epsilon大小为半径的球上面
                    param.data = self.project(name, param.data, self.epsilon)

    def restore(self, emb_name='word_embeddings'):
        """
        将模型原本参数复原
        :param emb_name: 模型中embedding的参数名
        """
        # 循环遍历每一个参数
        for name, param in self.model.named_parameters():
            # 如果当前参数在计算中保留了对应的梯度信息，并且包含了模型中embedding的参数名
            if param.requires_grad and emb_name in name:
                assert name in self.emb_backup
                # 取出模型真实参数
                param.data = self.emb_backup[name]
        # 清空emb_backup
        self.emb_backup = {}

    def project(self, param_name, param_data, epsilon):
        """
        控制扰动后的模型参数值
        :param param_name:
        :param param_data:
        :param epsilon:
        """
        # 计算加了扰动后的参数值与原始参数的差值
        r = param_data - self.emb_backup[param_name]
        # 如果差值的范数大于epsilon
        if torch.norm(r) > epsilon:
            # 对差值进行截断
            r = epsilon * r / torch.norm(r)
        # 返回新的加了扰动后的参数值
        return self.emb_backup[param_name] + r

    def backup_grad(self):
        """
        对梯度进行备份
        """
        # 循环遍历每一个参数
        for name, param in self.model.named_parameters():
            # 如果当前参数在计算中保留了对应的梯度信息
            if param.requires_grad:
                # 如果参数没有梯度
                if param.grad is None:
                    print("{} param has no grad !!!".format(name))
                    continue
                # 将参数梯度进行备份
                self.grad_backup[name] = param.grad.clone()

    def restore_grad(self):
        """
        将梯度进行复原
        """
        # 循环遍历每一个参数
        for name, param in self.model.named_parameters():
            # 如果当前参数在计算中保留了对应的梯度信息
            if param.requires_grad:
                # 如果没有备份
                if name not in self.grad_backup:
                    continue
                # 如果备份了，就将原始模型参数梯度取出
                param.grad = self.grad_backup[name]

# 实例初始化
pgd = PGD(model)
steps_for_at = 3
for batch_input, batch_label in data:
    # 正常训练
    loss = model(batch_input, batch_label)
    # 反向传播，得到正常的grad
    loss.backward() 
    # 保存正常的梯度
    pgd.backup_grad()
    # PGD要走多步，迭代走多步
    for t in range(steps_for_at):
        # 在embedding上添加对抗扰动, first attack时备份param.data
        pgd.attack(is_first_attack=(t == 0))
        # 中间过程，梯度清零
        if t != steps_for_at - 1:
            optimizer.zero_grad()
        # 最后一步，恢复正常的grad
        else:
            pgd.restore_grad()
        # embedding参数被修改，此时，输入序列得到的embedding表征不一样                     
    	loss_at = model(batch_input, batch_label)
        # 对抗样本上的损失
        loss_at = outputs_at[0]
        # 反向传播，并在正常的grad基础上，累加对抗训练的梯度
        loss_at.backward()
    # 恢复embedding参数
   	pgd.restore()
    # 梯度下降，更新参数
    optimizer.step()
    # 将梯度清零
    model.zero_grad()

---

如果对您有帮助，麻烦点赞关注，这真的对我很重要！！！如果需要互关，请评论或者私信！

---