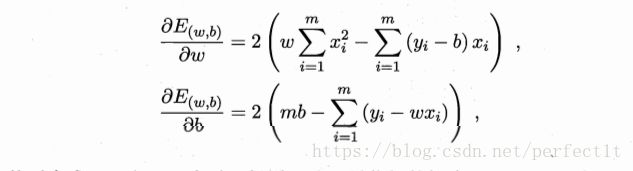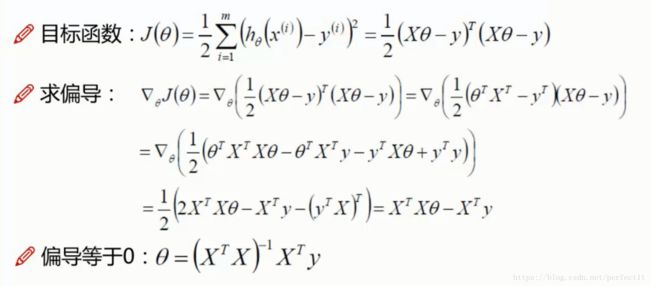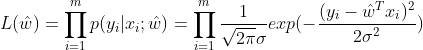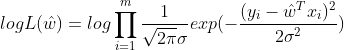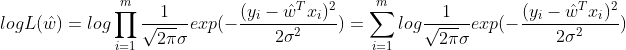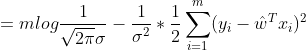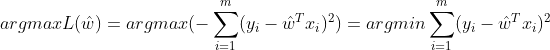David_Hdw

机器学习之线性回归（Linear Regression）

在数理统计中，线性回归是这样定义的：线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。

一、基本形式

线性模型的基本形式：给定由d个属性描述的示例 $x = ({x_1;x_2;..;x_d})$ ，其中 $x_i{}$ 是x在第i个属性上的取值，线性模型试图学到一个函数，该函数通过属性的线性组合来进行预测，表示为： ---- (1). 用向量表示为: ----- (2)，当学到w和b之后，模型就可以确定。

当只有一个样例时：

$w^T=\begin{bmatrix}1 \\ 2 \\ 3 \end{bmatrix}$ $x=\begin{bmatrix} 1&2 & 3 \end{bmatrix}$ ，f(x) = 14

当有多个样例时(以3为例)：

$w^T=\begin{bmatrix}1 \\ 2 \\ 3 \end{bmatrix}$ $x=\begin{bmatrix} [1 & 2 & 3]\\ [4 & 5 & 6]\\ [ 7& 8 & 9] \end{bmatrix}$ ，则 $f(x)=\begin{bmatrix} [14]\\ [32]\\ [50] \end{bmatrix}$

二、线性回归

现有数据集 $D=\left \{ (x_1,y_1),(x_2,y_2), ...,(x_m,y_m)_{} \right \}$ ,其中表示第i个样本，有d个属性， $y_i\epsilon R$ 。线性回归试图学得一个线性模型可以尽可能准确地预测实值输出标记，即输入为时，尽可能输出正确的。即试图学得 $f(x_i)=\textbf{w}^Tx_i+b$ ，使得 $f(x_i)\simeq y_i$ 。

(一）单元线性回归（输入属性的数目为1，即d=1）

对于单元线性回归，我们希望学得，使得 $f(x_i)\simeq y_i$ 。上面说过，当学到w和b之后，模型就可以确定。那么我们如何学到或者说确定w和b呢？学到模型目的是为了令预测值尽可能的与真实值相等，显然，如何确认w和b，关键在于我们如何衡量预测值f(x)于y之间的差别。均方误差是回归任务中最常用的性能度量，所以我们可以试图让均方误差最小化。

注：均方误差（mean-square error, MSE）是反映估计量与被估计量之间差异程度的一种度量。设t是根据子样确定的总体参数θ的一个估计量， $(\Theta -t)^2$ 的数学期望，称为估计量t的均方误差。

均方误差最小化，即

$(w*, b*) = \underset{(w,b)}{argmin}\ \frac{1}{2m} \sum_1^m(f(x_i)-y_i)^2=\underset{(w,b)}{argmin}\ \frac{1}{2m} \sum_1^m(y_i-wx_i-b)^2$

其中，w*和b*表示w和b的解。

均方误差有非常好的几何意义，对应了欧几里得距离。基于均方误差最小化来进行模型求解的方法称为最小二乘法。在线性回归中，最小二乘法就是试图找到一条直线，使所有的样本到直线上的欧氏距离之和最小。

我们将上面使均方误差最小化的过程，称为线性回归模型的最小二乘法“参数估计”。求解过程如下：

令 $E_(_w,_b_) = \frac{1}{2m} \sum_{i=1}^{m}(y_i-wx_i+b)^2$
将分别对w和b求导，得到：
令上述求导结果为零(极值点处，导数为零)，得到w和b的解：
其中 $\bar{x} = \frac{1}{m}\sum_{i=1}^{m}x_i$ 为x的均值。

如下图，其中蓝色打叉的点的集合为数据集，横坐标m^2为属性，纵轴为预测的值，单元线性回归主要学得的模型如第二幅图中的红色直线一样，而各个数据点到红色直线的距离的平方和的均值即为均方差，我们优化的目标或者想要学得的模型就是尽可能使点都落在线上(此处不考虑过拟合问题).

(二）多元线性回归(输入属性的数目有多个)

此时，如开头所说的数据集 $D=\left \{ (x_1,y_1),(x_2,y_2), ...,(x_m,y_m)_{} \right \}$ ,其中表示第i个样本，有d个属性， $y_i\epsilon R$ 。我们试图学得 $f(x_i)=\textbf{w}^Tx_i+b$ ，使得 $f(x_i)\simeq y_i$ 。这称为“多元线性回归”。

同理于单元线性回归，我们使用最小二乘法来对 $\textbf{w}$ 和.令数据集D表示为m*{d+1}大小的矩阵X，其中每行的最后一个元素都为1，即：

在把标签y也写成向量的形式： $\textbf{y}=(y_1;y_2;...;y_m)$ ，把 $\hat{w}=(w;b)$ 。则求解 $\hat{w}$ 的公式为：

$\hat{w}^* =\underset{\hat{w}}{argmin}(\textbf{y}-X\hat{w})^T(\textbf{y}-X\hat{w})$

上式求导公式为：

$\frac{\partial [(Xu-v)^T(Xu-v)]}{\partial X}=2(Xu-v)u^T$ 。

令导数等于0，即 $2X^T(X\hat{w-\textbf{y}})=0$ ，得到 $X^TX\hat{w} = X^T\textbf{y}$ ，两边左乘得 $\hat{w}^* =(X^TX)^-^1X^T\textbf{y}$ 。其中是的逆矩阵，只有当为满秩矩阵或正定矩阵时其才存在。令 $\hat{x_i}=(x_i;1)$ ，则最终学到的多元线性回归模型为：

$f(\hat{x_i})=\hat{x_i}^T(X^TX)^-^1X^T\textbf{y}$ 。

如下图，对于多元线性回归，学到的模型是一个超平面，红点的集合为数据集，均方误差为红色点到超平面的距离的平方和的均值，我们要学到的模型就是使红点尽可能的落在平面上（不考虑过拟合问题），下图输入属性为2.

然而，在现实的任务中往往不是满秩矩阵，那么此时可解出多个解 $\hat{w}$ ，均能使均方误差最小化。选择哪个解作为输出呢，将由学习算法的偏好决定，通常会通过引入正则化regularization项的方式。

三、从极大似然到最小二乘法

前面我们说过，线性回归试图学得 $f(x_i)=\textbf{w}^Tx_i+b$ ，使得 $f(x_i)\simeq y_i$ 。既然是约等号，那么就存在误差，假设每个样本i预测值真实值的误差为 $\varepsilon _i$ ，则有 $y_i=\hat{w}^Tx_i+\varepsilon _i$ 。

对于误差 $\varepsilon _i$ ：误差是独立并且具有相同的分布，并且服从均值为0方差为1的高斯分布。如下图：

由于误差服从上图的高斯分布，所以有

$p(\varepsilon_i)=\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(\varepsilon _i)^2}{2\sigma ^2})$

把 $y_i=\hat{w}^Tx_i+\varepsilon _i$ 带入其得，

$p(y_i|x_i;\hat{w})=\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\hat{w}^Tx_i)^2}{2\sigma ^2})$

则似然函数为:

$L(\hat{w}) =\prod_{i=1}^{m}p(y_i|x_i;\hat{w})=\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\hat{w}^Tx_i)^2}{2\sigma ^2})$

为方便计算，两边取对数得：

$logL(\hat{w}) =log\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\hat{w}^Tx_i)^2}{2\sigma ^2})$

由对数关系中乘法的特性得：

$logL(\hat{w}) =log\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\hat{w}^Tx_i)^2}{2\sigma ^2})=\sum_{i=1}^{m}log\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\hat{w}^Tx_i)^2}{2\sigma ^2})$

展开上式得：

$\sum_{i=1}^{m}log\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\hat{w}^Tx_i)^2}{2\sigma ^2})= \sum_{i=1}^{m}(log\frac{1}{\sqrt{2\pi}\sigma }+(-\frac{(y_i-\hat{w}^Tx_i)^2}{2\sigma ^2}))$

$= mlog\frac{1}{\sqrt{2\pi}\sigma }-\frac{1}{\sigma ^2}*\frac{1}{2}\sum_{i=1}^{m}(y_i-\hat{w}^Tx_i)^2$

我们的目标是让似然函数越大越好，因为常数对结果不产生影响，所以去掉常数。所以上式化简后且求最大有：

$argmaxL(\hat{w})=argmax(-\sum_{i=1}^{m}(y_i-\hat{w}^Tx_i)^2)=argmin\sum_{i=1}^{m}(y_i-\hat{w}^Tx_i)^2$

该式与最小二乘法一样。

四、实践

以下代码及数据集，可以去到博主的GitHub上，欢迎大家fork和star。

GitHub：https://github.com/davidHdw/machine-learning/tree/master

(一) 标准线性回归，即使用标准的最小二乘法得到的公式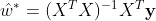 $\hat{w}^* =(X^TX)^-^1X^T\textbf{y}$ 进行求解参数w。

# -*- coding: utf-8 -*-

# regression.py

"""
Created on Fri Oct  5 10:47:15 2018

@author: david
"""

import numpy as np
import matplotlib.pyplot as plt

def loadDataSet(fileName):
    '''
    函数说明：数据导入函数
    参数：fileName: 数据存放的路径
    返回：dataMat: 数据特征集 
         labelMat: 数据标签集
    '''
    dataMat = []
    labelMat = []
    with open(fileName) as fr:
        numFeat = len(fr.readline().split("\t")) - 1
        for line in fr.readlines():
            lineArr = []
            curLine = line.strip().split('\t')
            for i in range(numFeat):
                lineArr.append(float(curLine[i]))
            dataMat.append(lineArr)
            labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

def standRegres(xArr, yArr):
    '''
    函数说明：标准回归函数（使用标准最小二乘法）
    参数: xArr: 不包括标签的训练集Array数组
         yArr: 训练集标签的Array数组
    返回：ws: 参数w的向量
    '''
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T       #转化成列向量
    # 按公式进行参数w的求解
    xTx = xMat.T * xMat
    if np.linalg.det(xTx) == 0.0:   # 行列式是否为0，是不能进行求逆
        print('This matrix is singular, cannot do inverse')
        return 
    ws = xTx.I * (xMat.T * yMat)    # 对公式进行计算
    print("ws:", ws)
    return ws
    
def plotDataSet():
    '''
    函数说明：绘制数据集
    参数：无
    返回：无
    '''
    xArr, yArr = loadDataSet("ex0.txt")     # 加载数据集
    n = len(xArr)                           # 获取数据长度
    xcord = []                              # 样本点
    ycord = []
    for i in range(n):
        xcord.append(xArr[i][1])            # xArr每行有一个偏置b和一个特征x
        ycord.append(yArr[i])               # yArr每行只有对应的值
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord, ycord, s=20, c='blue', alpha=0.5) # 描绘样本
    plt.title('DataSet')
    plt.xlabel("X")
    plt.show()

def plotRegression():
    '''
    函数说明：绘制回归曲线和数据点
    参数：无
    返回：无
    '''
    xArr, yArr = loadDataSet("ex0.txt")
    ws = standRegres(xArr, yArr)        # 调用标准回归函数获取回归参数ws
    xMat = np.mat(xArr)                 # 把array转成matrix
    yMat = np.mat(yArr)
    xCopy = xMat.copy()                 # 深拷贝xMat,得到xCopy，使的对xCopy操作时不影响xMat
    xCopy.sort(0)                       # 对数据集进行排序，从小到大
    yHat = xCopy * ws                   # 计算对应的回归y
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(xCopy[:,1], yHat, c = 'red')    # 画回归线
    # 描绘数据集个点，关于yMat.flatten.A[0]的意思：https://blog.csdn.net/lilong117194/article/details/78288795
    ax.scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0],
               s = 20, c = 'blue', alpha = .5)       
    plt.title("DataSet and Regression")
    plt.xlabel("X")
    plt.show()
    
    
if __name__ == "__main__":
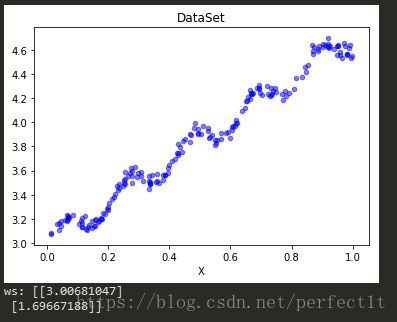
    plotDataSet()
    plotRegression()

其中，数据集如下左图，回归结果如下有图，红色线为回归得到的直线，蓝色为数据的点。

(二)局部加权线性回归

线性回归的一个问题是有可能出现欠拟合现象，因为他求的是具有最小均方误差的无偏估计。当出现欠拟合现象时，模型不能取得好的预测效果，所以可以通过一些方法在估计中加入(引入)一些偏差，从而降低预测的均方误差。其中一种方法为局部加权线性回归(Locally Weighted Linear Regression, LWLR)。其主要思想为：给待预测点附近的每个点赋予一定的权重，然后与标准回归类似，在该子集上基于最小均方误差来进行普通的回归。每次预测均需要事先取出对应的数据子集。此算法解出的回归参数的形式如：

$\hat{w}^* = (X^TW_eX)^-^1X^TW_ey$

其中是一个矩阵，用来给每个数据点赋予权重。

LWLR使用“核”(与支持向量机中的核类似)来对附近的点赋予更高的权重，该模型与kNN一样，认为样本点距离越近，越可能符合同一个线性模型，核可以自由选择，最常用的核就是高斯核，其对应的权重如下：

$w_e(i,i) = exp(\frac{|x_i-x|}{-2k^2})$ 。

构建了一个只包含对角线元素的权重矩阵。k决定了对附近的点赋予多大的权重。下面是代码：

# -*- coding: utf-8 -*-

# lwlr_regression.py

"""
Created on Fri Oct  5 15:59:57 2018

@author: 87955
"""

import numpy as np
import matplotlib.pyplot as plt

def loadDataSet(fileName):
    '''
    函数说明：数据导入函数
    参数：fileName: 数据存放的路径
    返回：dataMat:  数据特征集 
         labelMat: 数据标签集
    '''
    dataMat = []
    labelMat = []
    with open(fileName) as fr:
        numFeat = len(fr.readline().split("\t")) - 1
        for line in fr.readlines():
            lineArr = []
            curLine = line.strip().split('\t')
            for i in range(numFeat):
                lineArr.append(float(curLine[i]))
            dataMat.append(lineArr)
            labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

def lwlr(testPoint, xArr, yArr, k=1.0):
    '''
    函数说明：利用局部加权回归求解回归系数w,并且进行预测
    参数：
        testPoint : 测试样本点
        xArr :      x数据集
        yArr :      y数据集
        k :         高斯核的k,默认k=1.0
    返回：
        ws * testPoint : 测试样板点的测试结果        
    '''
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T       # 转换类型成matrix,并对其进行转置
    m = np.shape(xMat)[0]       # 样本数
    weights = np.mat(np.eye((m)))   #创建对角矩阵
    for i in range(m):
        diffMat = testPoint - xMat[i,:] # 当距离越远，则值越大，特征即坐标。
        weights[i,i] = np.exp(diffMat*diffMat.T / (-2.0*k**2)) # 成指数下降
    xTwx = xMat.T * (weights * xMat)                            ###############
    if np.linalg.det(xTwx) == 0:        #判断是否为0矩阵         # 按公式
        print("This matrix is singular, cannot do inverse")     # 进行参数
        return                                                  # w的求解
    ws = xTwx.I * (xMat.T * (weights * yMat))                   ###############
    return testPoint * ws

def lwlrTest(testArr, xArr, yArr, k=1.0):
    '''
    函数说明：局部加权回归测试
    参数：
        testArr: 测试集
        xArr:    x数据集
        yArr:    y数据集
        k:       高斯核中的k,默认为1.0
    返回：
        yHat:    测试结果集
    '''
    m = np.shape(testArr)[0]   #测试样本个数
    yHat = np.zeros(m)
    for i in range(m):                              # 对每个样本进行预测
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)   
    return yHat
    
def plotLwlrRegression():
    '''
    函数说明：绘制多条k不同的局部加权线性回归曲线
    参数：无
    返回：无
    '''
    xArr, yArr = loadDataSet("ex0.txt")
    yHat1 = lwlrTest(xArr, xArr, yArr, 1.0)         # 设置不同的k值进行预测
    yHat2 = lwlrTest(xArr, xArr, yArr, 0.01)
    yHat3 = lwlrTest(xArr, xArr, yArr, 0.003)
    xMat = np.mat(xArr)                             # 转化成matrix类型
    yMat = np.mat(yArr)
    sortInd = xMat[:,1].argsort(0)
    xSort = xMat[sortInd][:,0,:]        # 按照升序进行排序
    fig, axs = plt.subplots(nrows=3, ncols=1, sharex=False,
                            sharey=False, figsize=(10,8))
    
    axs[0].plot(xSort[:,1], yHat1[sortInd], c='red')    # 分别画出不同k值的回归曲线
    axs[1].plot(xSort[:,1], yHat2[sortInd], c='red')
    axs[2].plot(xSort[:,1], yHat3[sortInd], c='red')
    
    # 在3个子图中描绘样本点
    axs[0].scatter(xMat[:, 1].flatten().A[0], yMat.flatten().A[0],
       s = 20, c = 'blue', alpha = .5)
    axs[1].scatter(xMat[:, 1].flatten().A[0], yMat.flatten().A[0],
       s = 20, c = 'blue', alpha = .5)
    axs[2].scatter(xMat[:, 1].flatten().A[0], yMat.flatten().A[0],
       s = 20, c = 'blue', alpha = .5)
    
    # 设置标题，x轴label，y轴label
    axs0_title_text = axs[0].set_title('lwlr k=1.0')
    axs1_title_text = axs[1].set_title('lwlr k=0.01')
    axs2_title_text = axs[2].set_title('lwlr k=0.003')
    
    plt.setp(axs0_title_text, size=8, weight='bold',color='red')
    plt.setp(axs1_title_text, size=8, weight='bold',color='red')
    plt.setp(axs2_title_text, size=8, weight='bold',color='red')
    
    plt.xlabel("X")
    plt.show()
    

if __name__ == "__main__":
    plotLwlrRegression()

运行结果图：

图中可以看出来，当k=1.0时权重很大，如同将所有的数据视为等权重，得到的最佳拟合直线与标准的线性回归一样，可以看到其有些欠拟合；当k=0.01时权重得到了非常好的效果，抓住了数据的潜在模式；当k=0.003时纳入了太多的噪声点，拟合的直线与数据点过于贴近(过拟合)。

局部加权线性回归可以挖出数据潜在的规律，但局部线性回归也存在一个问题，可能你已经发现，局部加权线性回归增加了计算量，因为它对每个点做预测时都必须使用整个数据集。在k=0.01时可以得到很好的估计，但是看下图，当k=0.01时，发现大多数据点的权重都接近0，如果可以避免这些计算（降维），那么就可以减少运行时间，克服局部加权线性回归带来的增加计算量的问题。

(三) 缩减系数来“理解”数据

我们或多或少都会碰到这样的情况，数据的特征比样本点还多，此时还好能使用标准线性回归或局部加权线性回归的方法来做预测吗？肯定是不行的，该两种方法都会进行求逆，而当特征比样本点还多(n>m)，输入矩阵X不是满秩的，在计算会出错。为解决这个问题，下面将介绍几种方法：（1）岭回归；（2）lasso；（3）前向逐步回归。

1、岭回归

岭回归简单来说就是在矩阵上加一个 $\lambda I$ 从而使得矩阵非奇异，进而能对+ $\lambda I$ 进行求逆。I为n*n的单位矩阵,n代表特征数。则回归系数的计算公式变为：

$\hat{w}^*=(X^TX+\lambda I)^-^1X^Ty$

原先岭回归用来处理特征数比样本数多的情况，现也用于在估计中加入偏差，从而得到更好的估计。在这里通过引入 $\lambda$ 来限制了所有的w之和，用过引入该惩罚项，能够减少不重要的参数，在统计学中也叫缩减。

那么岭回归的是什么呢？岭回归使用了单位矩阵乘以常量 $\lambda$ ，看单位矩阵 I ，可以看到1贯穿整个对角线，其余元素为0。形象地，在0构成的平面上有一条1组成的“岭”。

下面看岭回归的实现代码：

# -*- coding: utf-8 -*-

# ridgeRegression.py

import numpy as np
import matplotlib.pyplot as plt

def rssError(yArr, yHatArr):
    """
    函数说明：求平方误差
    """
    return ((yArr-yHatArr)**2).sum()

def loadDataSet(fileName):
    '''
    函数说明：数据导入函数
    参数：fileName: 数据存放的路径
    返回：dataMat:  数据特征集 
         labelMat: 数据标签集
    '''
    dataMat = []
    labelMat = []
    with open(fileName) as fr:
        numFeat = len(fr.readline().split("\t")) - 1
        for line in fr.readlines():
            lineArr = []
            curLine = line.strip().split('\t')
            for i in range(numFeat):
                lineArr.append(float(curLine[i]))
            dataMat.append(lineArr)
            labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

def ridgeRegre(xMat, yMat, lam=0.2):
    '''
    函数说明：岭回归
    参数：
        xMat: x数据集
        yMat: y数据集
        lam:  缩减系数
    返回：
        ws : 岭回归的回归系数
    '''
    xTx = xMat.T * xMat                             # 按公式进行求解系数
    denom = xTx + np.eye(np.shape(xMat)[1]) * lam
    if np.linalg.det(denom) == 0.0:
        print("This matrix is singular, cannot do inverse")
        return 
    ws = denom * (xMat.T * yMat)
    return ws

def ridgeTest(xArr, yArr):
    '''
    函数说明：岭回归测试
    参数：
        xArr: x数据集
        yArr: y数据集
    返回：
        wMat : 回归系数
    '''
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    yMean = np.mean(yMat, axis = 0)    # axis=0,表示纵轴(列)，1代表横轴(行)，此处对列进行求平均
    yMat = yMat - yMean
    xMeans = np.mean(xMat, axis = 0)
    xVar = np.var(xMat, axis = 0)      # 求方差
    xMat = (xMat - xMeans) / xVar       # 进行归一化，使得变成标准化
    numTestPst = 30                     # 30个不同的lam进行测试
    wMat = np.zeros((numTestPst, np.shape(xMat)[1]))    # 初始化系数矩阵
    for i in range(numTestPst):
        ws = ridgeRegre(xMat, yMat, lam=np.exp(i-10))   # 对不同的lam值进行求解回归系数，lam以指数级变化，从很小的数开始
        wMat[i, :] = ws.T               # 对每个lam得到的回归系数进行保存
    return wMat

def plotwMat():
    '''
    函数说明：绘制岭回归系数矩阵
    参数：无
    返回：无
    '''
    abX, abY = loadDataSet("abalone.txt")
    ridgeWeights = ridgeTest(abX, abY)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(ridgeWeights)
    ax_title_text = ax.set_title('gaun xi')
    ax_xlabel_text = ax.set_xlabel('log(lambada)')
    ax_ylabel_text = ax.set_ylabel('ws')    
    plt.setp(ax_title_text, size=20, weight="bold", color = 'red')
    plt.setp(ax_xlabel_text, size=10, weight="bold", color = 'black')
    plt.setp(ax_ylabel_text, size=10, weight="bold", color = 'black')
    plt.show()
    
if __name__ == "__main__":
    plotwMat()

上面的代码，lambda以指数级进行变化，这样可以看出lambda在取非常小的值时和非常大的值时分别对结果造成的影响。最后将所有的具有不同的lambda的回归系数输出到一个矩阵上并返回。最后通过可视化lambda过回归系数的影响，发现当log(lambda)很小时，可以得到与所有系数的原始值(与标准线性回归一样)；当log(lambda)很大时，系数全部缩减为0；在合适的值可以得到较好的结果。

在增加如下约束时，普通最小二乘法回归会得到与岭回归一样的公式：

最小二乘法：

$\hat{w}^* =\underset{\hat{w}}{argmin}(\textbf{y}-X\hat{w})^T(\textbf{y}-X\hat{w})$

最小二乘法求解得到的结果：

$\hat{w}^* =(X^TX)^-^1X^T\textbf{y}$

增加的约束条件：

$\sum_{k=1}^{n}w_k^2\leq \lambda$

岭回归求解公式：

$\hat{w}^*=(X^TX+\lambda I)^-^1X^Ty$

上式的约束条件限定了所有的回归系数的平方和不能大于 $\lambda$ 。在使用普通的最小二乘法回归，当两个或更多的特征相关时，可能会得到一个很大的正系数和一个很大的负系数。因上式约束条件的存在，使得岭回归可以避免该问题。

注：该方法是使得系数趋向于0。

2、lasso回归

与岭回归类似，缩减方法lasso也对回归系数做了限定，其约束条件如下：

$\sum_{k=1}^{n}|w_k|\leq \lambda$

该约束条件与岭回归约束条件的不同的地方在于，该约束条件使用绝对值取代了平方和。其结果也与岭回归的结果大相径庭：在 $\lambda$ 足够小的时候，一些系数会因此被迫缩减到0。

3、前向逐步回归

前向逐步回归算法可以得到与lasso差不多的效果，但更加易于实现。属于贪心算法，即每一步都尽可能减少误差。主要工作为：一开始，所有的权重都设为1，然后每一步所做的决策是对某个权重增加或减少一个很小的值。

伪代码如下：

数据标准化，使其分布满足0均值和单位方差
    在每轮迭代过程中：
        设置当前最小误差为lowestError为正无穷
        对每个特征：
            增大或减小：
                改变一个系数得到新的w
                计算新w下的误差
                如果误差Error小于当前最小误差lowestError：
                    设置Wbest等于当前的W
            将W设置为新的Wbest

python实现如下：

# -*- coding: utf-8 -*-

# stageWiseRegression.py

import numpy as np
import matplotlib.pyplot as plt

def loadDataSet(fileName):
    '''
    函数说明：数据导入函数
    参数：fileName: 数据存放的路径
    返回：dataMat:  数据特征集 
         labelMat: 数据标签集
    '''
    dataMat = []
    labelMat = []
    with open(fileName) as fr:
        numFeat = len(fr.readline().split("\t")) - 1
        for line in fr.readlines():
            lineArr = []
            curLine = line.strip().split('\t')
            for i in range(numFeat):
                lineArr.append(float(curLine[i]))
            dataMat.append(lineArr)
            labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

def rssError(yArr, yHatArr):
    """
    函数说明：求平方误差
    """
    return ((yArr-yHatArr)**2).sum()

def regularize(xMat, yMat):
    '''
    函数说明：数据标准化，标准化：均值为0，方差为1
    参数：
        xMat : x数据集
        yMat : y数据集
    返回：
        inxMat : 标准化后的x数据集
        inyMat : 标准化后的y数据集
    '''
    inxMat = xMat.copy()            # 数据拷贝
    inyMat = yMat.copy()
    yMean = np.mean(inyMat, axis=0)     # 对列进行求均值
    inyMat = yMat - yMean               # 减去均值
    inMeans = np.mean(inxMat, axis=0)   # 对列进行求均值
    inVar = np.var(inxMat, axis=0)      # 对列进行求方差
    inxMat = (inxMat - inMeans) / inVar # 除以总方差，实现标准化
    return inxMat, inyMat
    
def stageWise(xArr, yArr, eps=0.01, numIt = 100):
    '''
    函数说明：前向逐步线性回归
    参数：
        xArr:  x输入数据
        yArr:  y预测数据
        eps:   每次调整的步长
        numIt: 迭代次数
    返回：
        returnMat:
    '''
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    xMat, yMat = regularize(xMat, yMat)     # 对数据进行标准化
    m,n = np.shape(xMat)
    returnMat = np.zeros((numIt, n))
    ws = np.zeros((n,1));
    wsTest = ws.copy()
    wsMax = ws.copy()
    for i in range(numIt):          # 迭代numIt次
        print(ws.T)
        lowestError = np.inf        # 每次迭代领最小误差为正无穷
        for j in range(n):          # 对每个特征
            for sign in [-1, 1]:    # 减或加   
                wsTest = ws.copy()
                wsTest[j] += eps * sign
                yTest = xMat * wsTest
                rssE = rssError(yMat.A, yTest.A) # 求总误差
                if rssE < lowestError :
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        returnMat[i, :] = ws.T      #记录numIt次迭代的回归系数矩阵
    return returnMat
    
def plotstageWiseMat():
	"""
	函数说明:绘制岭回归系数矩阵

	"""
	xArr, yArr = loadDataSet('abalone.txt')
	returnMat = stageWise(xArr, yArr, 0.005, 1000)
	fig = plt.figure()
	ax = fig.add_subplot(111)
	ax.plot(returnMat)	
	ax_title_text = ax.set_title('die dai ci shu yu hui gui xi shu de guan xi ')
	ax_xlabel_text = ax.set_xlabel('diedai cishu')
	ax_ylabel_text = ax.set_ylabel('huigui xishu')
	plt.setp(ax_title_text, size = 15, weight = 'bold', color = 'red')
	plt.setp(ax_xlabel_text, size = 10, weight = 'bold', color = 'black')
	plt.setp(ax_ylabel_text, size = 10, weight = 'bold', color = 'black')
	plt.show()


if __name__ == '__main__':
	plotstageWiseMat()

在鲍鱼数据上执行逐步线性回归法得到的系数与迭代次数间的关系，如下图所示：

图中上边的几行向量，就是最后几次迭代所得到的回归系数的值，可以看出第二个特征的系数为0，即该特征对预测结果不产生影响，而第五个特征的影响最大。

逐步线性回归算法的主要优点在于它可以帮助我们理解现有的模型并做出改进。当构建了一个模型后，可以运行该算法找出重要的特征，这样就有可能即时停止对那些不重要特征的收集。

当使用缩减法（如岭回归或前向逐步线性回归）时，模型也就增加了偏差(bias)，同时减小了模型的方差。

五、总结

1、基本形式：，用向量表示为:

2、单元线性回归模型为一条直线，多元线性回归模型为一个超平面。

3、均方误差是回归常用的性能度量，基于均方误差最小化的优化方法称为最小二乘法。

4、从极大似然到最小二乘法

5、标准线性回归的实现：

$\hat{w}^* =(X^TX)^-^1X^T\textbf{y}$

6、局部加权线性回归：

$\hat{w}^* = (X^TW_eX)^-^1X^TW_ey$

7、岭回归：

$\hat{w}^*=(X^TX+\lambda I)^-^1X^Ty$ ；

约束条件：