Deep CORAL: Correlation Alignment for Deep Domain Adaptation

本篇是迁移学习专栏介绍的第十六篇论文，由BU完成发表在ECCV2016上。

---

Abstract

深度神经网络能够从大量标记的输入数据中学习强大的表示，但是它们不能很好地概括输入分布的变化。提出了一种域自适应算法来补偿由于域移动而导致的性能下降。在本文中，我们解决了目标域未标记的情况，需要无监督的自适应。CORAL[1]是一种非常简单的无监督域自适应方法，它用线性变换对源和目标分布的二阶统计量进行对齐。在这里，我们将CORAL扩展到学习一个非线性转换，该转换将深层神经网络(deep CORAL)中的层激活关联对齐。在标准基准数据集上的实验显示了最先进的性能。

---

1 Introduction

许多机器学习算法都假设训练和测试数据是独立的，并且是同分布的。然而，这种假设在实践中很少成立，因为数据很可能随着时间和空间的变化而变化。虽然目前最先进的深卷积神经网络特征在一定程度上对低水平线索是不变的[2,3,4]，但是Donahue等人的[5]表明，它们仍然容易受到域移位的影响。非监督域自适应方法[6、7、8、9、10、1]试图通过将知识从标记源域转移到未标记目标域，来弥补性能的下降，而不是收集标记数据并为每种可能的场景训练一个新的分类器。最近提出的CORAL方法[1]对源分布和目标分布的二阶统计量进行线性变换。尽管它令人沮丧地简单，但对于无监督的领域适应工作得很好。然而，它依赖于线性变换，不是端到端的：它需要首先提取特征，应用变换，然后在单独的步骤中训练SVM分类器。

在这项工作中，我们通过构造一个可微损失函数，将CORAL的损失直接纳入到深层网络中，从而将CORAL损失的源相关性和目标相关性之间的差异最小化。与CORAL相比，我们提出的深CORAL方法学习了非线性转换更强大，并与深度CNNs无缝工作。我们在标准基准数据集上评估我们的方法，并展示最先进的性能。

---

2 Related Work

以前的无监督自适应技术包括重新加权训练点损失，以更紧密地反映测试分布中的那些损失[11,12]，或者在低维流形中找到一个转换，使源空间和目标子空间更接近。基于重加权的方法通常假定一种有限形式的域移位选择偏差，因此不适用于更一般的场景。测地线方法[13,7]通过将源和目标投影到沿测地线路径[13]上的点上，或者找到一个将源点转换为目标[7]的闭合形式线性映射，将源和目标区域连接起来。[14,8]通过计算线性映射来对齐子空间，该线性映射最小化了前n个特征向量之差的Frobenius范数。相比之下，CORAL[1]通过对源分布和目标分布的二阶统计数据进行比对，将域偏移最小化。

自适应深度神经网络是近年来发展起来的一种无监督自适应神经网络。DLID[15]通过两个适应层训练一个联合的源和目标CNN架构。DDC[16]将一个线性核应用于一个层，以最小化最大平均偏差(MMD)，而DAN[17]将多个核应用于多个层，从而最小化MMD。ReverseGrad[18]添加了一个二进制分类器来显式地混淆这两个域。

我们提出的Deep CORAL方法类似于DDC、DAN和ReverseGrad，即添加一个新的损失(CORAL损失)来最小化跨域学习特征协方差的差异，这类似于使用多项式核最小化MMD。然而，它比DDC更强大(DDC只对示例进行对齐)，比DAN和ReverseGrad更容易优化，并且可以无缝集成到不同的层或体系结构中。

---

3 Deep CORAL

我们解决了目标域中没有标记训练数据的无监督域适应场景，并建议利用预先在大型通用域(如Imagenet[19])上训练的深层特性和标记源数据。与此同时，我们还希望最终学习到的特性能够在目标领域很好地工作。第一个目标可以通过从通用的预训练网络初始化网络参数并对标记源数据进行微调来实现。对于第二个目标，我们建议最小化源和目标特征激活之间的二阶统计量差异，即CORAL损失。图1显示了使用我们提出的相关对齐层进行深度域适应的示例Deep CORAL架构。我们将深CORAL称为任何包含CORAL损失以适应区域变化的深CORAL网络。

3.1 CORAL Loss

我们首先描述单个特征层在两个域之间的CORAL损失。假设给定源域训练示例，未标记的目标数据。假设源数据和目标数据的数量分别为nS和nT。这里x和u都采用深层激活的输入，我们正在努力学习。假设表示第i个源(目标)数据样本的第j维数，表示特征协方差矩阵。

我们将CORAL损失定义为来源和目标特征的二阶统计量(协方差)之间的距离：

其中表示均方矩阵Frobenius的norm。源数据和目标数据的协方差矩阵由

其中1是所有元素都等于1的列向量。

利用链式法则可以计算出相对于输入特征的梯度：

我们使用批处理协方差，网络参数在两个网络之间共享。

3.2 End-to-end Domain Adaptation with CORAL Loss

以一个多类分类问题为例描述了该方法。如前所述，最终的深度特征既需要足够的判别性来训练强分类器，又要对源域和目标域之间的差异保持不变。最小化分类损失本身可能导致对源域的过度拟合，从而降低目标域的性能。另一方面，减少CORAL的损失可能会导致退化的特征。例如，该网络可以将所有源数据和目标数据投影到一个点，使CORAL的损失微不足道地为零。然而，没有一个强分类器可以建立在这些特征之上。同时进行分类损失和CORAL损失的联合训练，可能会学到在目标领域工作良好的特性：

其中t表示CORAL的数量损失层深度网络和λ是一个重量,交易的适应与分类精度在源域。如下图所示，这两种损失是对应的，并在训练结束时达到平衡，最终的特征有望在目标领域很好地工作。

---

4 Experiments

我们在一个标准的域自适应基准上对我们的方法进行了评估，该基准是Office数据集[6]。Office数据集包含来自办公环境的31个对象类别，分布在3个图像域中:Amazon、DSLR和Webcam。

我们遵循[7,17,5,16,18]的标准协议，使用所有有标签的源数据和所有没有标签的目标数据。由于有3个域，我们对所有6个移位都进行了实验，以一个域为源，另一个域为目标。

在本实验中，我们将CORAL loss应用到最后一个分类层，因为它是最普遍的情况，最深层的分类器架构(如convolutional、)包含一个完全连通的分类层。将CORAL损失应用到其他层或其他网络架构应该是很简单的。

最后一个全连接层(fc8)的维数设置为类别数(31)，初始化为N(0,0.005)。fc8的学习率是其他层的10倍，因为它是从零开始训练。我们使用在ImageNet[19]上预先训练的参数初始化其他层，并保留原始层layer-wise参数设置。在培训阶段，我们将批大小设置为128，基础学习率设置为，重量衰减为，动量设置为0.9。CORAL的重量损失(λ)设置这样的训练分类损失和CORAL损失大致相同。这似乎是一个合理的选择，因为我们希望有一个特征表示，既具有鉴别力，又能最小化源域和目标域之间的距离。我们所有的实验都使用了Caffe[21]和BVLC Reference CaffeNet。

我们比较了最近发表的7种方法:CNN [20] (no adaptation)、GFK[7]、SA[8]、TCA[22]、CORAL[1]、DDC[16]、DAN[17]。GFK、SA和TCA是基于流形的方法，它们将源和目标分布投影到低维流形中，而不是端到端的深度方法。DDC给AlexNet增加了一个域混淆损失，并对源域和目标域进行了微调。DAN类似于DDC，但它采用多内核选择方法来实现更好的平均嵌入匹配，适用于多层。为了直接比较，DAN在本文中使用了隐藏层fc8。对于GFK、SA、TCA和CORAL，我们在源域([1]中的ft7)上使用了经过微调的fc7特征，因为它比一般的预训练特征具有更好的性能，并训练了一个线性SVM[8,1]。为了进行公平的比较，我们使用其他作者在完全相同的设置下报告的准确性，或者使用作者提供的源代码进行实验。

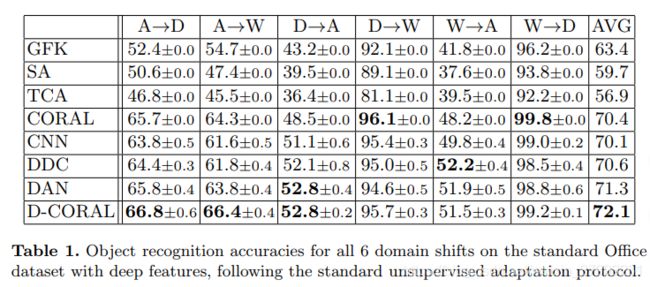
从表1可以看出，Deep CORAL (D-CORAL)的平均性能优于CORAL和其他6种基线方法。在6班中的3班，它达到了最高的精度。在其他3个偏移量中，D-CORAL与最佳基线方法之间的差值非常小(6 0.7)。

为了更好地理解Deep CORAL，我们为domain shift a w生成了三个图。在图2(a)中，我们显示了训练(源)和测试(目标)的准确性，用于有和没有CORAL丢失的训练。我们可以清楚地看到，添加CORAL loss有助于在目标域上获得更好的性能，同时在源域上保持较强的分类精度。

在图2(b)中，我们可视化了分类损失和训练w/ CORAL损失的CORAL损失。由于最后一个全连通层随机初始化为N(0,0.005)，初期CORAL损失很小，分类损失很大。经过几百次迭代的训练，这两个损失基本相同。在图2(c)中，我们显示了训练w/o CORAL损失域之间的CORAL距离(将权重设置为0)。我们可以看到距离变得越来越大(>是训练w/CORAL损失域的100倍)。对比图2(b)和图2(c)，我们可以看到，虽然CORAL的损失并不总是在训练过程中减少，但是如果我们将其权重设置为0，那么源域和目标域之间的距离就会变得大得多。这是合理的，因为没有域自适应的微调可能会使特性过度适合源域。CORAL的消失在微调过程中限制了源区和目标区的距离，并有助于维持平衡，使最终的特征在目标区域上工作得很好。

---

5 Conclusion

在这项工作中，我们扩展了CORAL，一个简单而有效的无监督域适应方法，以执行端到端适应的深度神经网络。在标准基准数据集上的实验显示了最先进的性能。Deep CORAL与Deep network无缝协作，可以轻松集成到不同的层或网络架构中。