数学建模算法与应用学习day2——非线性规划问题

以下内容来自司守奎编写的数学建模算法与应用学习，主要是记录自己的学习历程，转载还请标明出处！

一、非线性规划

知识点

3.1 非线性规划模型

3.1.1 非线性规划的实例与定义

3.1.2 非线性规划的MATLAB解法

%不完全代码（有点问题）
%非线性规划的MATLAB解法
function f = fun1(x);
f = sum(x^2) + 8;
function [g,h] = fun2(x);
g = [-x(1)^2 + x(2)^2 - x(3)^2
      x(1) + x(2)^2 + x(3)^3 - 20]; %非线性约束条件
h = [-x(1) - x(2)^2 + 2
      x(2) + 2*x(3)^2 - 3]; %非线性约束等式
[ x , y ] = fmincon( 'fun1' , rand(3,1) , [] , [], [], [], zeros(3,1) ,[] ,'fun2') 

3.2 无约束问题的MATLAB解法

3.2.1无约束极值问题的符号解

%有问题代码
clc ,  clear %暂时不太懂这句话的意思
syms x y %这个应该是定义变量？
f = x^3 - y^3 + 3*x^2 + 3*y^2 - 9*x;
df = jacobian(f); %求一阶偏导数
d2f = jacobian(df); %求hessian阵
[xx,yy] = solve(df) %求驻点
xx = double(xx); yy = double(yy);%转化成双精度浮点型数据，下面判断特征值的正负，必须是数值型数据
for i = 1 : length(xx) 
    a = subs( d2f ,{ x,y} ,{ xx(i) , yy(i) } );
    if all(b>0) 
        fprintf('(% f, % f)是极小值点，对应的极小值为 % f\n',xx(i),yy(i),f);
    elseif all(b<0)
        fprintf('(% f, % f)是极大值点，对应的极大值为 % f\n',xx(i),yy(i),f);
    elseif any(b>0) & any(b<0)
        fprintf('(% f, % f)不是极值点\n',xx(i),yy(i));
    else fprintf('无法判断(%f,%f)是否是极值点\n',xx(i),yy(i));
    end
end

3.2.2无约束极值问题的数值解

3.2.3求函数的零点和方程组的解

3.3 约束极值问题

约束极值问题目的就是为了化非线性规划问题为线性规划问题。

3.3.1 二次规划

以上需注意实对称矩阵的定义

MATLAB中求解二次规划的命令是：
[x,fval] = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)

注：MATLAB中的help quadporg后的帮助文档。

上面的那个程序须注意的是实对称矩阵得自己先行求解出来！（这里有个问题，关于x的实对称矩阵的求解）

3.3.2 罚函数法

这一个方法有点难度，没有太懂。

罚函数法又称序列无约束最小化技术SUMT

罚函数法分为两种：一种是外罚函数法，一种是内罚函数法

几个概念的理解：
罚函数
增广目标函数

3.3.3 MATLAB求约束极值问题

求解最优化问题的函数有：fminbnd、fmincon、quadprog、fseminf、fminmax。



例题3-12没有看懂，有几处的语法不太懂。

例题3-14中的目标函数的梯度没有理解，第一个式子理解，就是高数中的梯度，但是第二个式子怎么来的不知道

3.3.4 MATLAB优化工具箱的用户图形界面算法

重点：MATLAB中的optimtool命令提供了优化问题的用户图形界面解法。
实质上就是省掉一部分程序，让用户用起来更加方便。

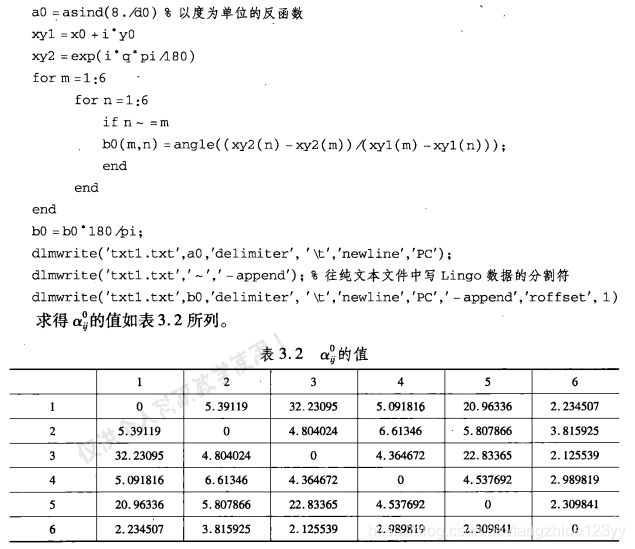
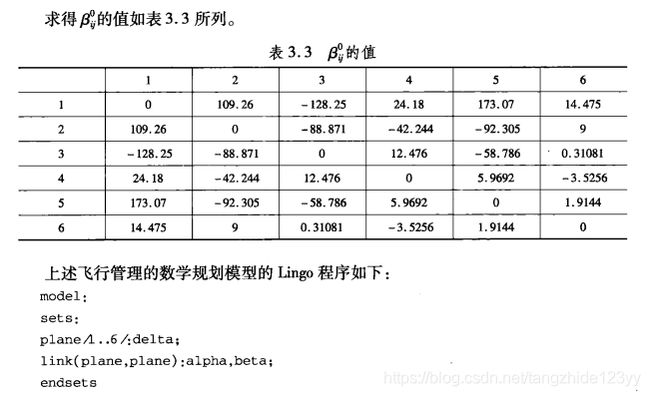
3.4 飞行管理问题

这个飞行管理问题应该算是上面所有的线性以规划及非线性规划问题的总和运用。

有两种思路：第一种是利用相对速度，相对夹角。另一种就是在xoy坐标系中，利用数学表达式，确定每时每刻飞机的各种参数。

3.4.1 模型一

3.4.2 模型二

习题