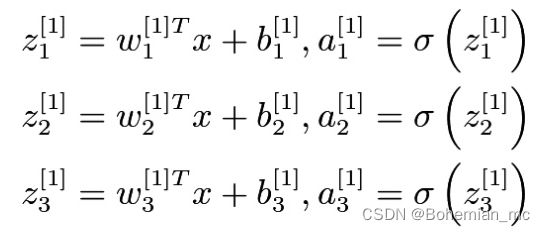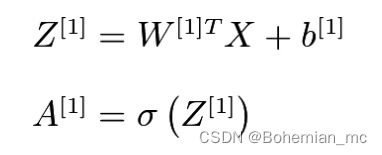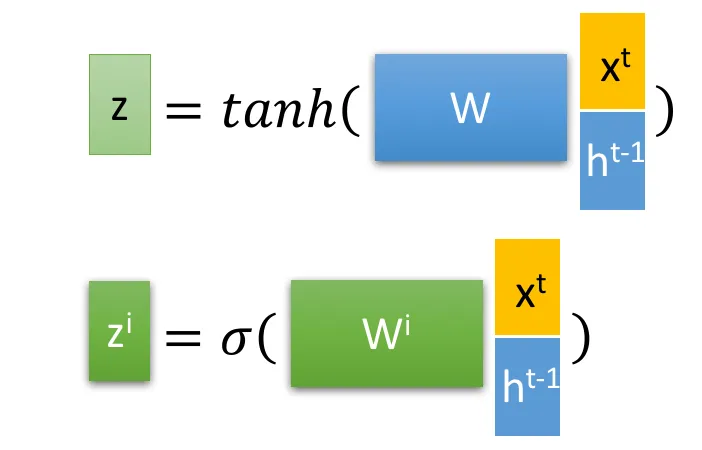【学习周报】研究生学习周报
这周主要研读了HMN中reference的一篇论文TRL,经过学习对比发现TRL中的很多思想都在HMN中有所借鉴,看完TRL后对HMN中的一些问题理解也更加的透彻;因为这周需要集中对深度学习基础进行学习,因此回顾复习了一些深度学习的基础知识。
学习内容:
- Object Relational Graph with Teacher-Recommended Learning for Video Captioning(CVPR2020)
- 浅层神经网络
- 深层神经网络
- LSTM
学习时间:
- 10.3 ~ 10.8
学习笔记:
1.浅层神经网络:
每当我们听到神经网络时,就会认为它里面有许许多多的隐藏层,但其实还有一种只有少量隐藏层的神经网络,浅神经网络只包含一到两层隐藏层。对浅神经网络的研究可以加强我们对深度神经网络内部运行机制的理解。下图所示是一个只包含一个隐藏层、一个输入层和一个输出层的浅神经网络:
1.1神经元
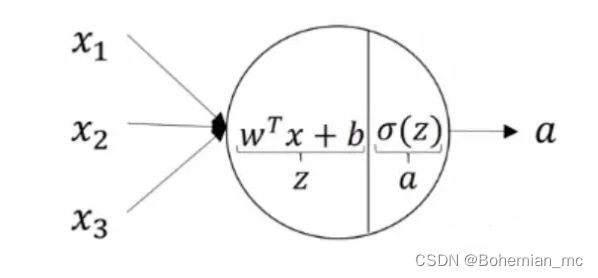
神经元是神经网络中的原子单元。给定神经元一个输入,它将得到对应的输出,并将其作为下一层的输入。一个神经元可以认为是以下两部分的结合:
- 第一部分根据输入和权重来计算得到Z 。
- 第二部分在Z上施加激活函数得到神经元的最终输出A。
1.2隐藏层
隐藏层由许多神经元组成,每一个都会执行上述两步运算。在上图的浅层神经网络中,隐藏层的四个神经元进行如下计算:
在上面的方程中:
- 下标i表示第i层,下标j表示该层的第j个神经元。
- X是包含3个特征的输入向量。
- W[i]j是第i层第j个神经元的权值。
- b[i]j 是第i层第j个神经元的偏置。
- Z[i]j 是第i层第j个神经元的中间输出。
- A[i]j 第i层第j个神经元的最终输出。
- Sigma 是sigmoid激活函数。
显而易见,上述四个方程比较冗长,因此我们把它们进行向量化:
- 第一个方程用一个矩阵乘法计算所有的中间输出Z。
- 第二个方程用一个矩阵运算计算所有的激活函数输出A。
2.深层神经网络
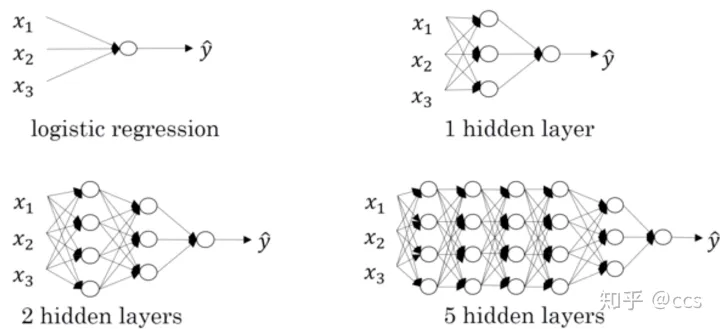
对于人脸识别等应用,神经网络的第一层从原始图片中提取人脸的轮廓和边缘,每个神经元学习到不同边缘的信息;网络的第二层将第一层学得的边缘信息组合起来,形成人脸的一些局部的特征,例如眼睛、嘴巴等;后面的几层逐步将上一层的特征组合起来,形成人脸的模样。随着神经网络层数的增加,特征也从原来的边缘逐步扩展为人脸的整体,由整体到局部,由简单到复杂。层数越多,那么模型学习的效果也就越精确。
通过例子可以看到,随着神经网络的深度加深,模型能学习到更加复杂的问题,功能也更加强大。
2.1深层神经网络的表示
2.2前向传播
以单个样本来进行表示,每层经过线性计算和激活函数两步计算
z [ 1 ] = W [ 1 ] x + b [ 1 ] , a [ 1 ] = g [ 1 ] ( z [ 1 ] ) z^{[1]}=W^{[1]}x+b^{[1]},a^{[1]}=g^{[1]}(z^{[1]}) z[1]=W[1]x+b[1],a[1]=g[1](z[1])
z [ 2 ] = W [ 2 ] a [ 1 ] + b [ 2 ] , a [ 2 ] = g [ 2 ] ( z [ 2 ] ) z^{[2]}=W^{[2]}a^{[1]}+b^{[2]},a^{[2]}=g^{[2]}(z^{[2]}) z[2]=W[2]a[1]+b[2],a[2]=g[2](z[2])
z [ 3 ] = W [ 3 ] a [ 2 ] + b [ 3 ] , a [ 3 ] = g [ 3 ] ( z [ 3 ] ) z^{[3]}=W^{[3]}a^{[2]}+b^{[3]},a^{[3]}=g^{[3]}(z^{[3]}) z[3]=W[3]a[2]+b[3],a[3]=g[3](z[3])
z [ 4 ] = W [ 4 ] a [ 3 ] + b [ 4 ] , a [ 4 ] = g [ 4 ] ( z [ 4 ] ) z^{[4]}=W^{[4]}a^{[3]}+b^{[4]},a^{[4]}=g^{[4]}(z^{[4]}) z[4]=W[4]a[3]+b[4],a[4]=g[4](z[4])
将上式简单的用通用公式表达出来:
z [ L ] = W [ L ] a [ L − 1 ] + b [ L ] , a [ L ] = g [ L ] ( z [ L ] ) z^{[L]}=W^{[L]}a^{[L-1]}+b^{[L]},a^{[L]}=g^{[L]}(z^{[L]}) z[L]=W[L]a[L−1]+b[L],a[L]=g[L](z[L]),输入 a [ L − 1 ] a^{[L-1]} a[L−1],输出 a [ L ] a^{[L]} a[L]
2.3反向传播
单个样本的反向传播:
d Z [ l ] = d J d a [ l ] d a [ l ] d Z [ l ] = d a [ l ] ∗ g [ l ] ′ ( Z [ l ] ) dZ^{[l]}=\frac{dJ}{da^{[l]}}\frac{da^{[l]}}{dZ^{[l]}}=da^{[l]}*{g^{[l]}}'(Z^{[l]}) dZ[l]=da[l]dJdZ[l]da[l]=da[l]∗g[l]′(Z[l])
d W [ l ] = d J d Z [ l ] d Z [ l ] d W [ l ] = d Z [ l ] ∗ a [ l − 1 ] dW^{[l]}=\frac{dJ}{dZ^{[l]}}\frac{dZ^{[l]}}{dW^{[l]}}=dZ^{[l]}*a^{[l-1]} dW[l]=dZ[l]dJdW[l]dZ[l]=dZ[l]∗a[l−1]
d b [ l ] = d J d Z [ l ] d Z [ l ] d b [ l ] = d Z [ l ] db^{[l]}=\frac{dJ}{dZ^{[l]}}\frac{dZ^{[l]}}{db^{[l]}}=dZ^{[l]} db[l]=dZ[l]dJdb[l]dZ[l]=dZ[l]
d a [ l − 1 ] = W [ l ] T ⋅ d Z [ l ] da^{[l-1]}=W^{[l]T}\cdot dZ^{[l]} da[l−1]=W[l]T⋅dZ[l]
多个样本的反向传播:
d Z [ l ] = d A [ l ] ∗ g [ l ] ′ ( Z [ l ] ) dZ^{[l]}=dA^{[l]}*{g^{[l]}}'(Z^{[l]}) dZ[l]=dA[l]∗g[l]′(Z[l])
d W [ l ] = 1 m d Z [ l ] ⋅ A [ l − 1 ] T dW^{[l]}=\frac{1}{m}dZ^{[l]}\cdot A^{[l-1]T} dW[l]=m1dZ[l]⋅A[l−1]T
d b [ l ] = 1 m n p ⋅ s u m ( d Z [ l ] , a x i s = 1 ) db^{[l]}=\frac{1}{m}np\cdot sum(dZ^{[l]},axis=1) db[l]=m1np⋅sum(dZ[l],axis=1)
d A [ l ] = W [ l + 1 ] T ⋅ d Z [ l + 1 ] dA^{[l]}=W^{[l+1]T}\cdot dZ^{[l+1]} dA[l]=W[l+1]T⋅dZ[l+1]
2.4参数与超参数
参数
参数即是我们在过程中想要模型学习到的信息(模型自己能计算出来的),例如 W [ l ] , b [ l ] W^{[l]},b^{[l]} W[l],b[l]。而超参数(hyper parameters)即为控制参数的输出值的一些网络信息(需要人经验判断)。超参数的改变会导致最终得到的参数 W [ l ] , b [ l ] W^{[l]},b^{[l]} W[l],b[l]的改变。
超参数
典型的超参数有:
- 学习速率: α α α
- 迭代次数: N N N
- 隐藏层的层数: L L L
- 每一层的神经元个数: n [ 1 ] , n [ 2 ] n^{[1]},n^{[2]} n[1],n[2]
- 激活函数的选择: g ( z ) g(z) g(z)
参数初始化
如果在初始时将两个隐藏神经元的参数设置为相同的大小,那么两个隐藏神经元对输出单元的影响也是相同的,通过反向梯度下降去进行计算的时候,会得到同样的梯度大小,所以在经过多次迭代后,两个隐藏层单位仍然是对称的。无论设置多少个隐藏单元,其最终的影响都是相同的,那么多个隐藏神经元就没有了意义。
在初始化的时候,W 参数要进行随机初始化,不可以设置为 0。b 因为不存在上述问题,可以设置为 0。
3.LSTM
3.1什么是LSTM
长短期记忆(Long short-term memory, LSTM)是一种特殊的RNN,主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说,就是相比普通的RNN,LSTM能够在更长的序列中有更好的表现。
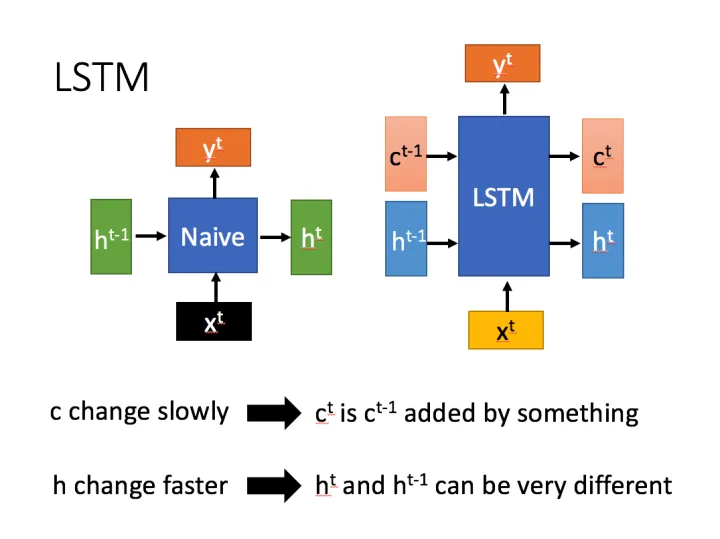
LSTM结构(图右)和普通RNN的主要输入输出区别如下所示。
相比RNN只有一个传递状态 h t h^t ht ,LSTM有两个传输状态,一个 c t c^t ct(cell state),和一个 h t h^t ht(hidden state)。(Tips:RNN中的 h t h^t ht 对于LSTM中的 c t c^t ct )
其中对于传递下去的 c t c^t ct 改变得很慢,通常输出的 c t c^t ct 是上一个状态传过来的 c t − 1 c^{t-1} ct−1 加上一些数值。
而 h t h^t ht 则在不同节点下往往会有很大的区别。
3.2深入LSTM结构
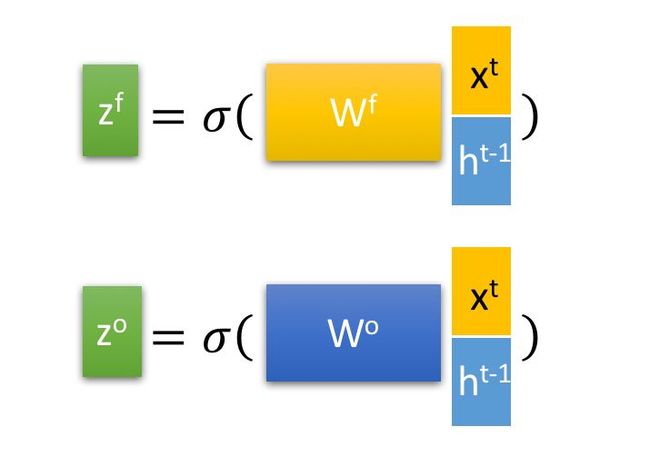
首先使用LSTM的当前输入 x t x^t xt 和上一个状态传递下来的 h t − 1 h^{t-1} ht−1 拼接训练得到四个状态。
其中, z f , z i , z o z^f,z^i,z^o zf,zi,zo 是由拼接向量乘以权重矩阵之后,再通过一个 s i g m o i d sigmoid sigmoid 激活函数转换成0到1之间的数值,来作为一种门控状态。而 z z z 则是将结果通过一个 t a n h tanh tanh 激活函数将转换成-1到1之间的值(这里使用 t a n h tanh tanh 是因为这里是将其做为输入数据,而不是门控信号)。
⊙ \odot ⊙是矩阵对应元素相乘,要求两个相乘矩阵是同型的。 ⊕ \oplus ⊕是矩阵对应元素相加。
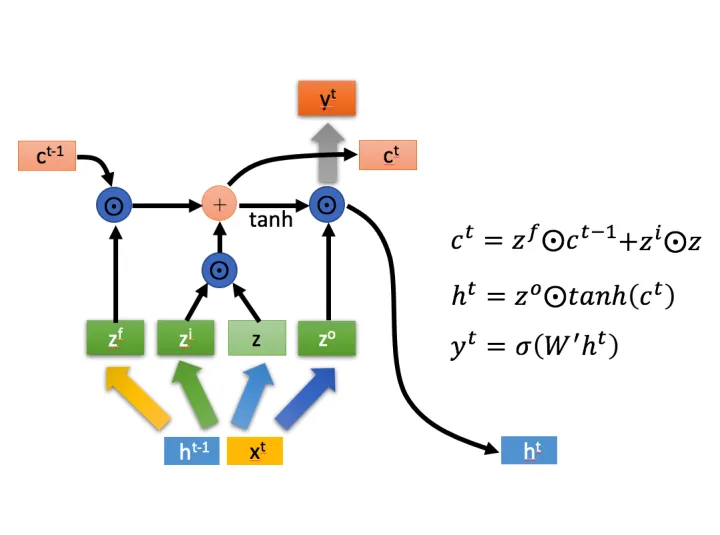
LSTM内部主要有三个阶段:
- 忘记阶段。这个阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的,记住重要的”。具体来说是通过计算得到的 z f z^f zf(f表示forget)来作为忘记门控,来控制上一个状态的 c t − 1 c^{t-1} ct−1 哪些需要留哪些需要忘。
- 选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入 x t x^t xt 进行选择记忆。哪些重要则着重记录下来,哪些不重要,则少记一些。当前的输入内容由前面计算得到的 z z z 表示。而选择的门控信号则是由 z i z^i zi(i代表information)来进行控制。
- 输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过 z o z^o zo 来进行控制的。并且还对上一阶段得到的 c o c^o co 进行了放缩(通过一个tanh激活函数进行变化)。
与普通RNN类似,输出 y t y^t yt 往往最终也是通过 h t h^t ht 变化得到。
3.3总结
以上,就是LSTM的内部结构。通过门控状态来控制传输状态,记住需要长时间记忆的,忘记不重要的信息;而不像普通的RNN那样仅有一种记忆叠加方式。对很多需要“长期记忆”的任务来说,尤其好用。但也因为引入了很多内容,导致参数变多,也使得训练难度加大了很多。