文章目录
- 基于Python的数学建模
- 空间插值
-
- 基本概念
- Scipy一维插值
- Scipy多维插值方法
- 反距离权重插值(IDW)
- 克里金插值(Kriging)
基于Python的数学建模
- Github仓库:Mathematical-modeling
空间插值
基本概念
- 定义:空间插值常用于将离散的测量数据转换为连续的数据曲面,以便与其它空间现象的分布模式进行比较,它包括了空间内插和外推两种算法。
- 空间内插算法:通过已知点的数据推求同一区域未知点数据
- 空间外推算法:通过已知区域的数据,推求其它区域数据
- 区别:
- 是处理方法不同、职责不同、工作内容不同
- 内插法在样本数据的范围内预测,比外插法要准。
- 用回归方程预测范围以外的数值称为外插法,而内插法是对数据范围内的点进行预测。
- 插值分类
- 整体插值、局部插值和边界内插法
- 确定性插值和地统计插值
- 精确插值和近似插值
- 插值工具:
scipy.interpolate 模块有一维插值函数(interp1d)、二位插值函数(interp2d)、多纬插值函数(interpn、interpnd),可以进行使用常见的方法进行插值。例如线性插值,最近邻插值和样条插值。PyKrige包可以提供各种类型的kriging插值
Scipy一维插值
- 生成已知数据点集
(x,y)和需要插值的新数据集xnew
np.random.seed(666)
x = np.linspace(0, 10, 20)
y = np.cos(x) * 2 + np.sin(x) / 2
xnew = np.linspace(0, 10, 50)
- 通过不同插值方法,根据给定数据点集
(x,y)来计算插值函数 f ( x ) f(x) f(x)
f1 = interp1d(x, y, kind="linear")
f2 = interp1d(x, y, kind="nearest")
f3 = interp1d(x, y, kind="nearest-up")
f4 = interp1d(x, y, kind="zero")
f5 = interp1d(x, y, kind="slinear")
f6 = interp1d(x, y, kind="quadratic")
f7 = interp1d(x, y, kind="cubic")
f8 = interp1d(x, y, kind="previous")
f9 = interp1d(x, y, kind="next")
- 不同空间插值方法对比
fig, [[ax1,ax2],[ax3,ax4]] = plt.subplots(2,2,figsize=(12,8))
ax1.plot(x,y,'o',label='已知数据点')
ax1.plot(xnew,f1(xnew),'r',label='线性插值')
ax1.legend()
ax2.plot(x,y,'o',label='已知数据点')
ax2.plot(xnew,f2(xnew),label='最临近点插值-向下取舍')
ax2.plot(xnew,f3(xnew),label='最临近点插值-向上取舍')
ax2.legend()
ax3.plot(x,y,'o',label='已知数据点')
ax3.plot(xnew,f4(xnew),label='零阶样条插值')
ax3.plot(xnew,f5(xnew),label='一次样条插值')
ax3.plot(xnew,f6(xnew),label='二次样条插值')
ax3.plot(xnew,f7(xnew),label='三次样条插值')
ax3.legend()
ax4.plot(x,y,'o',label='已知数据点')
ax4.plot(xnew,f8(xnew),label='前点插值')
ax4.plot(xnew,f9(xnew),label='后点插值')
ax4.legend()

Scipy多维插值方法
- 生成已知数据点集
(x,y,z)和需要插值的新数据集xnew,ynew
def func(x, y):
return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2
rng = np.random.default_rng()
points = rng.random((1000, 2))
values = func(points[:,0], points[:,1])
xnew, ynew = np.linspace(0,1,200), np.linspace(0,1,200)
xnew_grid, ynew_grid = np.meshgrid(xnew, ynew)
- 通过不同插值方法,根据给定数据点集
(x,y,z)来计算插值函数 f ( x , y ) f(x,y) f(x,y)
from scipy.interpolate import griddata
xi = (xnew_grid, ynew_grid)
z1 = griddata(points, values, xi, method="nearest")
z2 = griddata(points, values, xi, method="linear")
z3 = griddata(points, values, xi, method="cubic")
- 不同空间插值方法对比
fig, [[ax1, ax2], [ax3, ax4]] = plt.subplots(2,
2,
subplot_kw=dict(projection='3d'),
figsize=(12, 10))
ax1.scatter3D(points[:, 0], points[:, 1], values)
ax1.set_title('原始数据')
ax2.scatter3D(xnew_grid, ynew_grid, z1)
ax2.set_title('最近邻插值')
ax3.scatter3D(xnew_grid, ynew_grid, z2)
ax3.set_title('线性插值')
ax4.scatter3D(xnew_grid, ynew_grid, z3)
ax4.set_title('三次样条插值')

反距离权重插值(IDW)
- IDW算法的Python实现
def IDW(xnewgrid,ynewgrid,x, y, z, b=2):
"""
:param xnew: 网格化的插值点x
:param ynew: 网格化的插值点y
:param x: 已知数据点x
:param y: 已知数据点y
:param z: 已知数据点z
:return: 插值结果
"""
xnewgrid_, ynewgrid_ = xnewgrid.ravel(), ynewgrid.ravel()
znew = []
for i in range(len(xnewgrid_)):
d = np.sqrt((xnewgrid_[i]-x)**2 + (ynewgrid_[i]-y)**2)
if 0 in d:
znew.append(z[np.where(d == 0)[0][0]])
else:
distance = 1 / (d**b)
distance_sum = np.sum(distance)
distance_weight = distance / distance_sum
znew.append(np.sum(distance_weight * z))
znew = np.array(znew)
znew = znew.reshape(xnewgrid.shape)
return znew
- 生成已知数据点集
(x,y,z)和需要插值的新数据集xnew,ynew
def func(x, y):
return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2
x = np.linspace(-10, 10, 20)
y = np.linspace(-10, 10, 20)
z = func(x, y)
xnew = np.linspace(-10, 10, 50)
ynew = np.linspace(-10, 10, 50)
xnew_grid, ynew_grid = np.meshgrid(xnew, ynew)
- 计算插值结果
znew = IDW(xnew_grid,ynew_grid,x, y, z, b=2)
fig, [ax1, ax2] = plt.subplots(1,2,subplot_kw=dict(projection='3d'),figsize=(10, 8))
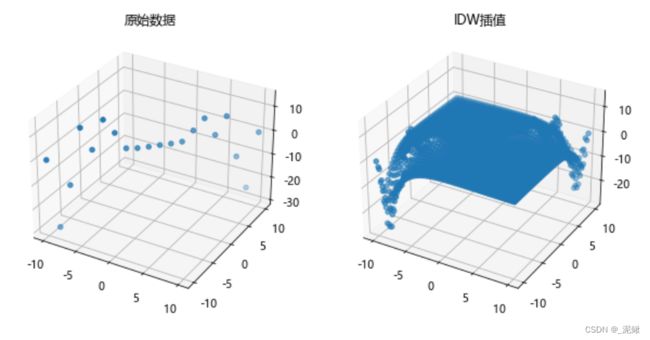
ax1.scatter3D(x,y,z)
ax1.set_title('原始数据')
ax2.scatter3D(xnew_grid, ynew_grid, znew)
ax2.set_title('IDW插值')
克里金插值(Kriging)
- 生成已知数据点集
(x,y,z)和需要插值的新数据集xnew,ynew
def func(x, y):
return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2
x = np.linspace(-10, 10, 20)
y = np.linspace(-10, 10, 20)
z = func(x, y)
xnew = np.linspace(-10, 10, 50)
ynew = np.linspace(-10, 10, 50)
xnew_grid, ynew_grid = np.meshgrid(xnew, ynew)
- 克里金插值(Kriging)插值
from pykrige.ok import OrdinaryKriging
OK = OrdinaryKriging(
x,
y,
z,
variogram_model="linear",
)
znew, ss = OK.execute("grid", xnew, ynew)
fig, [ax1, ax2] = plt.subplots(1,2,subplot_kw=dict(projection='3d'),figsize=(10, 8))
ax1.scatter3D(x,y,z)
ax1.set_title('原始数据')
ax2.scatter3D(xnew_grid, ynew_grid, znew)
ax2.set_title('克里金插值')




