论文笔记之Distributed Representations of Words and Phrases and their Compositionality

这篇文章是用于解决skip-gram和CBOW两种模型在计算softmax时因为语料库V太大导致计算复杂度偏高的问题。为了降低复杂度，提高运算效率，论文作者提出了层次softmax以及负采样的方式去解决(负采样会比层次softmax用的更多些)。此外，作者还提出了一种重采样方式去使得采样更偏重一些含重要信息的词。

参考：
①B站视频
②论文
③Word2vec的两种原模型
④Word2vec 中的数学原理详解
⑤Word2Vec-知其然知其所以然

文章介绍了2种可以简化skip-gram和CBOW两种模型中softmax部分的计算复杂度，即Hierarchical Softmax(HS)和Negative Sampling(NS)。这两种技巧均可用于上述2种模型，故HS和NS的目标就是改变softmax的表达式：
$$p(o|c)=\frac{exp(u_o^T{v}_c)}{{\sum }_{w=1}^{V}exp(u_w^T{v}_c)}\text{\hspace{1em}(1)}$$
从式(1)中可以看出，计算一次概率需要经过$V$(语料库大小)次的指数运算，那么自然HS和NS就要想办法在保证求出概率$p(o|c)$的情况下，减小$u_w^T{v}_c$的运算次数。因此原skip-gram以及CBOW的softmax需要做出改进。

1 Hierarchical Softmax

层次softmax的核心思想就是通过引出二叉树结构(Huffmax 二叉树)将求softmax的计算转为求sigmoid的计算，从而将计算复杂度从$V$降到$lo{g}_{2}V$以下，即从原来的需要求$V$次关于$u_w^T{v}_c$的指数运算降低到求小于$lo{g}_{2}V$次的sigmoid运算($sigmoid:\sigma (x)=\frac{1}{1+e^{-x}}$)。

为了便于理解，我们中间加入满二叉树过程而不是直接到Huffman树过程。

上图是一个满二叉树(V=8)，可以看到，每次计算一个词$a$的概率需要进行$lo{g}_{2}V=3$次的二分类过程，也就是说需要进行3次的sigmoid计算。

那么满二叉树达到了$lo{g}_{2}V$的优化程度，那么有没有更快的方式呢？——引入Huffman树。

哈夫曼树是带权重路径最短二叉树，它基于将权值小的节点放的位子深(越小越接近叶子节点)，权值大的节点放的位子浅(越大越靠近根节点)的原则来实现比满二叉树更小的路径和。
Note:

1. 在层次softmax的CBOW和skip-gram模型中，你无法采用$\frac{W+W^{\ast }}{2}$的形式来做，因为在skip-gram模型中，只有一组完整的中心词向量矩阵$W$，而中心词向量矩阵是由$\theta$组成的，其维度势必小于$V$，故$W$和$W^{\ast }$是size不同的两个矩阵。同理，在CBOW模型中，只有一组完整的周围词向量矩阵$W$，而$W^{\ast }$的size是比$W$要小的，故不能相加。
2. 对于HS，有的词概率计算用的sigmoid次数可能小于$lo{g}_{2}V$，有的可能要大于$lo{g}_{2}V$，平均下来是$lo{g}_{2}V$。

1.1 Skip-gram HS构建

Skip-gram中哈夫曼树的构建：

1. 输出层是一课Huffman树。
2. 叶子节点是语料库中的词。
3. 将某个词出现的频率作为叶子节点的权值，频率越大的层数越浅，频率越小的层数越深。

如上图所示，比如说我们要去求"词I"的概率，我们用HS技巧来取代softmax计算，设c为中心词：
$$\begin{gathered} p(I|c)=\sigma ({\theta }_0^T{v}_c)\cdot \sigma ({\theta }_1^T{v}_c)\cdot (1-\sigma ({\theta }_2^T{v}_c)) \\ =\sigma ({\theta }_0^T{v}_c)\cdot \sigma ({\theta }_1^T{v}_c)\cdot \sigma (-{\theta }_2^T{v}_c)\text{\hspace{1em}(2)} \end{gathered}$$

1. $\theta$参数的个数一定是小于$V$的，其没有具体意义，实在要一个意义的话，可以理解为该节点以下整一簇的上下文词向量。
2. $\theta$的个数大约有$lo{g}_{2}V$个，比$V$要略大。
3. 树的高度大约是$O({\log }_{2}V)$。

上图的意思大概就是：从根节点出发，以一半一半的概率走向两个子节点，需要注意的是同一层的两个结点之和为1。然后一半一半的概率继续往下走，当第三次分开走的时候就遇到了我们要求的“词I”，我们把它拿出来做反向传播就行了。具体写成公式如下：
$$p(w|w_I)=\prod _{j=1}^{L(w)-1}\sigma (\delta (n(w,j+1)==ch(n(w,j)))\cdot {\theta }_{n(w,j)}^T{v}_{w_I})\text{\hspace{1em}(3)}$$
Note:

1. $n(w,j)$表示词$w$在树上的第j个节点，比如$n(w,1)$就是根节点。
2. $\delta (n(w,j+1)==ch(n(w,j)))$表示当节点$n(w,j)$的右儿子节点是词$w$的下一个节点的时候，那么就取正号，否则就取负号。
3. 公式(3)中$v_{w_I}$表示中心词向量。

1.2 CBOW HS的构建

在CBOW中HS和skip-gram中差不多，只是公式上略微有点变化。因为和skip-gram相反，CBOW要改变中心词向量矩阵$W^{\ast }$，具体如下：

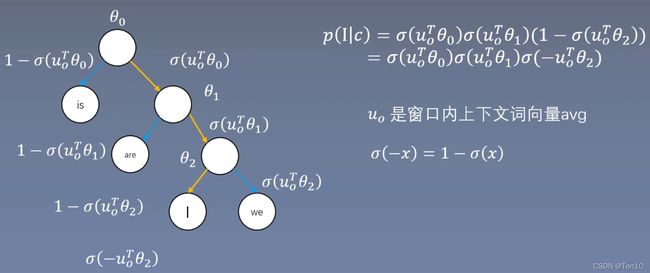
1. 如上图所示，$\theta$在CBOW中的含义大概是中心词向量，而非skip-gram中的上下文词向量。

对应skip-gram中的公式3，CBOW也要略微进行修改：
$$p(w|w_I)=\prod _{j=1}^{L(w)-1}\sigma (\delta (n(w,j+1)==ch(n(w,j)))\cdot u_{w_I}^T{\theta }_{n(w,j)})\text{\hspace{1em}(4)}$$

2 Negative Sampling

负采样的核心思想就是将多分类(V类)问题转为二分类问题。Softmax之所以慢，是因为它涉及一个多分类问题，且和词表大小$V$相关的。负采样就是舍弃多分类，转为二分类来提升速度。

2.1 Skip-gram中的NS

既然是二分类，正样本由中心词以及窗口内上下文词组成；负样本由中心词和词库中随意采样的样本组成。
先给出负采样的核心公式，即目标函数：
$$J_{neg-sample}(\theta )=log\sigma (u_o^T{v}_c)+\sum _{k=1}^K{\mathbb{E}}_{k\sim P(w)}[log\sigma (-u_k^T{v}_c)]\text{\hspace{1em}(5)}$$

1. $v_c$是中心词向量；$u_o$是窗口内上下文词向量；$u_k$是负采样上下文词向量。
2. 我们的目标是最大化式(5)，即正样本的$u_o^T{v}_c$概率越大越好；负样本$u_k^T{v}_c$越小越好。这也是二分类的核心思想：增大正样本概率，减小负样本概率。
3. 对于每个词，一次要输出$K+1$个概率，一般也不大(3~10)，所以会比Hierarchical Softmax需要计算大约$lo{g}_{2}V$个概率或者原模型需要的$V$个概率要高效很多。
4. 我们之所以取期望$\mathbb{E}$以及采取多个负样本，就是因为负样本是采样得来的，需要多采样几份求平均。
5. NS里面还是需要完整的$W$和$W^{\ast }$，故总的参数比HS要多，但是每次的计算量不多。

2.2 CBOW中的NS

大多数和skip-gram中的NS类似，除了正负样本的定义以及目标函数。
正样本由中心词及其窗口内上下文词的平均组成；负样本窗口内上下文词的平均和随机采样的词组成。
其目标函数为：
$$J_{neg-sample}(\theta )=log\sigma (u_o^T{v}_c)+\sum _{k=1}^K{\mathbb{E}}_{k\sim P(w)}[log\sigma (-u_o^T{v}_k)]\text{\hspace{1em}(6)}$$
Note:

1. $u_o$是窗口内上下文词向量；$v_c$是正确的中心词向量；$v_k$是错误的中心词向量。

如何采样呢？

1. 采样的核心思想就是减小频率大的词的采样概率，增加概率小的词的采样概率。之所以这么做，是因为概率小的词往往比较重要，反之概率大的词不太重要，如“the、a、to、的”。

3 Subsampling of Frequent Words

自然语言共识：在语料库中出现频率高的词往往不太重要，所含信息较少，如“a、and、the”；在语料中出现频率低的词往往比较重要，所含信息比较多。
重采样的原因：

1. 更多地训练重要的词对，比如训练“Chinese”和“HangZhou”的关系，少训练“Chinese”和“the”之间的关系。
2. 高频词很快就训练好了，而低频词需要训练更多的轮次。

重采样方式：
$$P(w_i)=max(0,1-\sqrt{\frac{t}{f(w_i)}}).$$

1. 其中$f(w_i)$为词$w_i$在数据集中出现的概率。文中选取$t=10^{-5}$，训练集中的词$w_i$会以$P(w_i)$的概率删除。
2. 词频越大，$f(w_i)$越大，$P(w_i)$越大，那么词$w_i$就有更大的概率被删除。
3. 实验表明，重采样可以加加速训练，得到更好的词向量。

4 实战演练

实战部分基于Negative Sampling的Skip-gram模型。
Pytorch库

4.1 PTB数据集

语料库：PTB数据集

PTB数据集主要是三个.txt文件：ptb_test.txt、ptb_train.txt、ptb_valid.txt。其中ptb_train.txt文件部分截图如上所示，其每一行都是一句话，便于直接读取。其中句尾符为，生僻词为，数字则用N表示。
训练部分我们将读取ptb_train.txt文件，其中共有887521个单词。

4.2 模型训练

数据预处理：
由于窗口的大小是随机选取的，因此不同中心词对应的上下文词的长度是不一样的，但是负采样值的长度和上下文词是一样的，这样就导致了训练过程中数据不对齐，我们可以采用补0的形式，然后用掩码去解决0带来的影响，让补0部分不参与训练。
其中前向推断如下：

中心词：(batch,1)
上下文词+负采样值：（batch，S）
Embding层：(词表大小N，D)——调用nn.Embding类
中心词向量：（batch，1， D）
周围词向量矩阵：（batch， S，D）
Label和来自中心词向量和周围词向量的乘积做二分类交叉熵Loss。

Note：

1. 在batch个中心词向量中，每一个中心词对应一个长度为S的，由周围词和负采样值以及掩码组成，因此这就相当于一个中心词对应窗口内的周围词都做了运算。
2. 这里和之前写的那篇Word2Vec笔记中不一样的一点是，并没有从索引到one-hot，再用矩阵乘法输出中心词向量，而是直接将索引通过Embding层挑选出指定索引对应的中心词向量。
3. 最后我们所想要的就是上图绿色Embding层的weight参数。

5 Conclusion

从模型复杂度理论对比以及实验来看：

1. CBOW和skip-gram都比NNLM或者RNNLM要快。
2. CBOW要比skip-gram计算要快一些。
3. 当$K$不超过14时候，负采样要比层次softmax要高效。