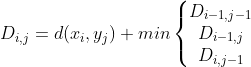DTW学习笔记1.0

 目录

DTW算法的目的：

DTW算法实现：

以下图两段序列为例：

DTW代码实现：

Dynamic programming function

示例：

单变量示例：

 比较序列相似性示例：

缺点：

---

DTW算法的目的：

1.计算两段序列的相似度

例如通过计算序列距离来判断右边三段序列哪段与左侧序列相似度最大

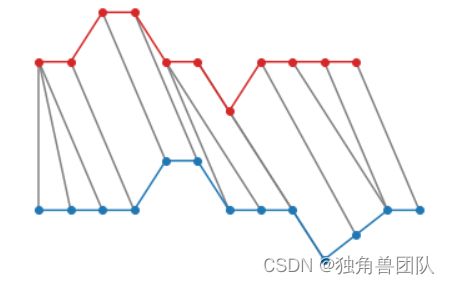
2.对两段序列实现点对点匹配（如下图所示）

DTW算法实现：

1.输入两段序列的长度：x:N and y:M

2.创建累计距离矩阵：

3.初始化累计矩阵：

       for i = 1 to N:   

       for j = 1 to M:  

4.计算累计矩阵：

for i = 1 to N:

        for j = 1 to M:

                           

（ 其中为距离函数，可采用欧式距离、余弦距离等等）

5.匹配路径：Trace back from  to 

以下图两段序列为例：

x = np.array([0, 2, 0, 1, 0, 0])
y = np.array([0, 0, 0.5, 2, 0, 1, 0])

 1. x序列长度N=6，y序列长度M=7

2. 创建累计距离矩阵并初始化（其中纵轴代表x序列，横轴代表y序列）：

累计矩阵D

∞
∞
∞
∞
∞
∞
0	∞	∞	∞	∞	∞	∞	∞

3. 填充累计距离矩阵：

设距离函数

根据公式依次填充上方累计距离矩阵，

∞	3	3	3.5	5	1.5	2.5	0.5
∞	3	3	3	4.5	1.5	1.5	0.5
∞	3	3	2.5	3	1.5	0.5	1.5
∞	2	2	2	2.5	0.5	1.5	1.5
∞	2	2	1.5	0.5	2.5	3.5	5.5
∞	0	0	0.5	2.5	2.5	3.5	3.5
0	∞	∞	∞	∞	∞	∞	∞

序列距离=D(6,7)=0.5

4.匹配路径

从右上角D(6,7)开始回溯，选择其（左方，下方，左下方）最小值的位置，直至到左下方D(0,0)

DTW代码实现：

Preliminaries

from matplotlib.patches import ConnectionPatch
import matplotlib.pyplot as plt
import numpy as np
import scipy.spatial.distance as dist

Dynamic programming function

def dp(dist_mat):
 
    N, M = dist_mat.shape
    
    # 初始化累计距离矩阵cost_mat
    cost_mat = np.zeros((N + 1, M + 1))
    for i in range(1, N + 1):
        cost_mat[i, 0] = np.inf
    for i in range(1, M + 1):
        cost_mat[0, i] = np.inf

    # 填充累计距离矩阵cosy_mat并记录匹配路径信息traceback_mat
    traceback_mat = np.zeros((N, M))
    for i in range(N):
        for j in range(M):
            penalty = [
                cost_mat[i, j],      # match (0)
                cost_mat[i, j + 1],  # insertion (1)
                cost_mat[i + 1, j]]  # deletion (2)
            i_penalty = np.argmin(penalty)   #记录矩阵中每项周围最小值的位置
            cost_mat[i + 1, j + 1] = dist_mat[i, j] + penalty[i_penalty]
            traceback_mat[i, j] = i_penalty

    # 从矩阵右上方开始回溯
    i = N - 1
    j = M - 1
    path = [(i, j)]
    while i > 0 or j > 0:
        tb_type = traceback_mat[i, j]
        if tb_type == 0:
            # Match
            i = i - 1
            j = j - 1
        elif tb_type == 1:
            # Insertion
            i = i - 1
        elif tb_type == 2:
            # Deletion
            j = j - 1
        path.append((i, j))

    # 返回前去除累计距离矩阵的初始化边沿
    cost_mat = cost_mat[1:, 1:]
    return (path[::-1], cost_mat)

示例：

单变量示例：

x = np.array([0, 0, 1, 1, 0, 0, -1, 0, 0, 0, 0])
y = np.array([0, 0, 0, 0, 1, 1, 0, 0, 0, -1, -0.5, 0, 0])

# 创建距离矩阵
N = x.shape[0]
M = y.shape[0]
dist_mat = np.zeros((N, M))
for i in range(N):
    for j in range(M):
        dist_mat[i, j] = abs(x[i] - y[j])

# 使用上面DTW函数
path, cost_mat = dp(dist_mat)
print("x、y两条序列距离: {:.4f}".format(cost_mat[N - 1, M - 1]))
print(f"匹配路径：{path}")

输出结果：

x、y两条序列距离: 0.5000
匹配路径：[(0, 0), (0, 1), (0, 2), (1, 3), (2, 4), (3, 5), (4, 6), (4, 7), (5, 8), (6, 9), (7, 10), (8, 11), (9, 11), (10, 12)]

根据匹配路径，我们可以将xy两条序列各点对齐

 比较序列相似性示例：

a = np.array([0, 0, 1, 1, 0, 0, -1, 0, 0, 0, 0])
b = np.array([0, 0, 0, -1, -1, 0, 0, 0, 0.5, 0, 0, 0, 0])
c = np.array([0, 0, 0.25, 1, 0, 0.5, 0])
d = np.array([0, 0, 0, 0, 1, 1, 0, 0, 0, -1, -0.5, 0, 0])

for cur_b in [b, c, d]:

    # 距离矩阵
    N = a.shape[0]
    M = cur_b.shape[0]
    dist_mat = np.zeros((N, M))
    for i in range(N):
        for j in range(M):
            dist_mat[i, j] = abs(a[i] - cur_b[j])

    # DTW
    path, cost_mat = dp(dist_mat)
    print("Alignment cost: {:.4f}".format(cost_mat[N - 1, M - 1]))

输出结果：

Alignment cost: 2.5000
Alignment cost: 1.7500
Alignment cost: 0.5000

显然，序列d与序列a之间的距离最小，故认为序列d与序列a最相似

缺点：

DTW算法存在“病态对齐”现象

例如，对于上述相似性比较示例中，添加一条新序列e

e = np.array([0, 1, 0, -1, 0])

 计算序列a、e之间的距离结果：

Alignment cost: 0.0000

此时对于序列d，序列e反而与序列a最为相似，甚至序列距离为0

这是因为序列a、e对齐过程中出现多处“多对一”或者“一对多”情况，导致匹配路径path过长

             

 因此，为了防止这种“bug”出现，我们需要对匹配路径长度进行限制，也就是对DTW算法进行优化

这就引出了LDTW和FDTW算法（具体参考DTW学习笔记2.0）

参考文章：

lecture_dtw_notebook/dtw.ipynb at main · kamperh/lecture_dtw_notebook · GitHub