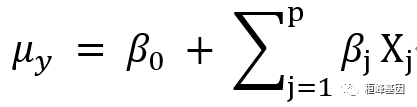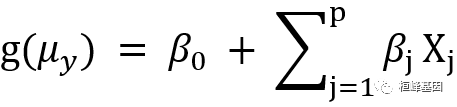Topic 4. 临床预测模型构建 Logistic 回归
上期我们已经基本了解变量的类型,以及如果处理不同种类的变量,现在我们就来学些一个临床预测模型–GLM 广义线性模型及 R 语言实现。
广义线性模型 (Generalized Linear Model) 是一般线性模型的推广,它使因变量的总体均值通过一个非线性连接函数而依赖于线性预测值,允许响应概率分布为指数分布族中的任何一员。许多广泛应用的统计模型都属于广义线性模型,如常用于研究二元分类响应变量的Logistic 回归、Poisson 回归和负二项回归模型等。一个广义线性模型包含以下三个部分:
①随机成分;
②线性成分;
③连接函数。
- 线性模型的扩展
-
结果变量是类别型:二分变量和多分类变量,显示都不是正太分布;
-
结果变量是数值型:非负有限值,且均值和方差都是相关的(正态分布之间是相互独立的);
-
广义线性模型扩展了线性模型的框架,包含了非正常因变量的分析。
- 标准线性模型公式
现要对响应变量 Y 和 p 个预测变量 X1···Xp。间的关系进行建模。在标准线性模型中,可假设 Y 呈正态分布,关系的形式为:
该等式表明响应变量的条件均值是预测变量的线性组合。参数 β,指一单位 X;的变化造成的 Y 预期的变化,β0指当所有预测变量都为 0 时 Y 的预期值。对于该等式,你可通俗地理解为:给定一系列 X 变量的值,赋予 X 变量合适的权重,然后将它们加起来,便可预测 Y 观测值分布的均值。
- 广义线性模型公式
上式中并没有对预测变量 Xj 做任何分布的假设。与 Y 不同,它们不需要呈正态分布。实际上,它们常为类别型变量(比如方差分析设计)。另外,对预测变量使用非线性函数也是允许的,比如你常会使用预测变量 X2 或者X1xX2,只要等式的参数(βo,β1,··,βp)为线性即可。广义线性模型公式为:
其中 g(μy) 是条件均值的函数(称为连接函数)。另外,你可放松 Y 为正态分布的假设,改为Y服从指数分布族中的一种分布即可。设定好连接函数和概率分布后,便可以通过最大似然估计的多次迭代推导出各参数值。
- glm (generalized linear model) 函数的使用
R 中可通过 glm() 函数拟合广义线性模型。它的形式与 lm() 类似,只是多了一些参数。函数的基本形式为:
glm(formula, family=family(link=function), data=)
每种相应分布(指数分布族)允许各种关联函数将均值和线性预测器关联起来,常用如下:
-
binomal(link=‘logit’) ----响应变量服从二项分布,连接函数为logit,即logistic回归;
-
binomal(link=‘probit’) ----响应变量服从二项分布,连接函数为probit;
-
poisson(link=‘identity’) ----响应变量服从泊松分布,即泊松回归。
glm() 函数中的连接函数,下表列出概率分布(family)和相应的默认函数(function),如下表:
- glm() 可连接的函数
glm() 可连接的函数与分析标准线性模型时lm()连用的许多函数在glm()中都有对应的形式,其中常见的函数如下:
-
summary() 展示拟合模型的细节;
-
coefficients()、coef() 列出拟合模型的参数(戳距项和斜率);
-
confint() 给出模型参数的置信区间(默认为95%);
-
residuals() 列出拟合模型的残差值;
-
anova() 生成两个拟合模型的方差分析表;
-
plot() 生成评价拟合模型的诊断图;
-
predict() 用拟合模型对新数据集进行预测;
-
deviance() 拟合模型的偏差;
-
df.residual() 拟合模型的残差自由度。
- Logistic 回归模型概述
Logistic 回归模型是一种概率模型它是以某一事件发生与否的概率 P 为因变量,以影响 P的因素为自变量建立的回归模型,分析某事件发生的概率与自变量之间的关系,是一种非线性回归模型。
Logistic 回归模型适用适用于因变量为:
-
二项分类
-
多项分类(有序、无序)的资料。
- Logistic 回归模型分类
-
条件Logistic回归模型:适合于配对或配伍设计资料;
-
非条件Logistic回归模型:适合于成组设计的统计资料;
-
因变量可以是:两项分类、无序多项分类、有序多项分类等。
- Logistic 回归案例–变量筛选方式
-
R 中可进行以下变量筛选方式,最终筛选出独立影响因素。:
-
用 Enter 法把所有自变量全纳入(不做筛选);
-
用逐步回归筛选自变量 (step()函数);
-
先做单因素 Logistic 回归,p<0.1纳入最后的回归方程;
- 实例操作
下面仍然以肠癌 colon 数据为例子做 Logistic 回归模型,并进行后续的模型评价以及图形展示。
- 数据处理
#%>% 数据处理方式需要加载一个dplyr的R包
library(survival) # cox回归模型需要
library(dplyr) # 处理数据需要2. 加载演示数据集
data(colon)# 加载数据集
str(colon) # 查看数据集结构
'data.frame': 1858 obs. of 16 variables:
$ id : num 1 1 2 2 3 3 4 4 5 5 ...
$ study : num 1 1 1 1 1 1 1 1 1 1 ...
$ rx : Factor w/ 3 levels "Obs","Lev","Lev+5FU": 3 3 3 3 1 1 3 3 1 1 ...
$ sex : num 1 1 1 1 0 0 0 0 1 1 ...
$ age : num 43 43 63 63 71 71 66 66 69 69 ...
$ obstruct: num 0 0 0 0 0 0 1 1 0 0 ...
$ perfor : num 0 0 0 0 0 0 0 0 0 0 ...
$ adhere : num 0 0 0 0 1 1 0 0 0 0 ...
$ nodes : num 5 5 1 1 7 7 6 6 22 22 ...
$ status : num 1 1 0 0 1 1 1 1 1 1 ...
$ differ : num 2 2 2 2 2 2 2 2 2 2 ...
$ extent : num 3 3 3 3 2 2 3 3 3 3 ...
$ surg : num 0 0 0 0 0 0 1 1 1 1 ...
$ node4 : num 1 1 0 0 1 1 1 1 1 1 ...
$ time : num 1521 968 3087 3087 963 ...
$ etype : num 2 1 2 1 2 1 2 1 2 1 ...
mycolon <- colon %>%
transmute(time, status,
Age = age,
Sex = factor(sex, levels = c(0,1), labels = c("Female", "Male")),
Obstruct = factor(colon$obstruct),
Differ = factor(colon$differ),
Extent = factor(colon$extent)
)
str(mycolon)
'data.frame': 1858 obs. of 7 variables:
$ time : num 1521 968 3087 3087 963 ...
$ status : num 1 1 0 0 1 1 1 1 1 1 ...
$ Age : num 43 43 63 63 71 71 66 66 69 69 ...
$ Sex : Factor w/ 2 levels "Female","Male": 2 2 2 2 1 1 1 1 2 2 ...
$ Obstruct: Factor w/ 2 levels "0","1": 1 1 1 1 1 1 2 2 1 1 ...
$ Differ : Factor w/ 3 levels "1","2","3": 2 2 2 2 2 2 2 2 2 2 ...
$ Extent : Factor w/ 4 levels "1","2","3","4": 3 3 3 3 2 2 3 3 3 3 ...
- 构建Logistic 回归模型
fit.full <- glm(status ~ Age + Sex + Obstruct + Differ + Extent,
binomial(link="logit"),
data = mycolon
)
summary(fit.full)
Call:
glm(formula = status ~ Age + Sex + Obstruct + Differ + Extent,
family = binomial(link = "logit"), data = mycolon)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6401 -1.1635 -0.6875 1.1829 1.7821
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.178450 0.462241 -2.549 0.010790 *
Age -0.002182 0.004004 -0.545 0.585738
SexMale -0.043452 0.095669 -0.454 0.649689
Obstruct1 0.190504 0.121687 1.566 0.117460
Differ2 0.008928 0.160204 0.056 0.955559
Differ3 0.413460 0.191356 2.161 0.030720 *
Extent2 0.580586 0.408774 1.420 0.155518
Extent3 1.285277 0.384588 3.342 0.000832 ***
Extent4 1.798638 0.449425 4.002 6.28e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2511.9 on 1811 degrees of freedom
Residual deviance: 2456.0 on 1803 degrees of freedom
(因为不存在,46个观察量被删除了)
AIC: 2474
Number of Fisher Scoring iterations: 4
从上面的结果我们可以从系数表中看出 Differ 和 Extent 显著,并系数表下面是拟合指数,包括无效和偏差残差以及AIC,接下来我们选取显著的两个变量再次做 logistics 模型,如下:
# fit reduced model
fit.reduced <- glm(status ~ Differ + Extent,
binomial(link="logit"),
data = mycolon
)
summary(fit.reduced)
Call:
glm(formula = status ~ Differ + Extent, family = binomial(link = "logit"),
data = mycolon)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5799 -1.1778 -0.6931 1.1770 1.7575
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.3043428 0.3979682 -3.278 0.001047 **
Differ2 0.0004684 0.1598019 0.003 0.997661
Differ3 0.4100279 0.1909961 2.147 0.031810 *
Extent2 0.5821058 0.4080007 1.427 0.153658
Extent3 1.3048701 0.3836668 3.401 0.000671 ***
Extent4 1.8039282 0.4489013 4.019 5.86e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2511.9 on 1811 degrees of freedom
Residual deviance: 2459.2 on 1806 degrees of freedom
(因为不存在,46个观察量被删除了)
AIC: 2471.2
Number of Fisher Scoring iterations: 4
- 模型比较
首先我们从两个模型的 AIC 可以看出第二个模型比较好,很多人只是看到AIC,并没深入了解,我大概说下意义:AIC信息准则即 Akaike information criterion ,是衡量统计模型拟合优良性 (Goodness of fit) 的一种标准,由于它为日本统计学家赤池弘次创立和发展的,因此又称赤池信息量准则。它建立在熵的概念基础上,可以权衡所估计模型的复杂度和此模型拟合数据的优良性。但是也可通过ANOVA检验比较两个模型的性能,P 值为0.36,差异并不显著如下:
# compare models
anova(fit.reduced, fit.full, test = "Chisq")
#Analysis of Deviance Table
#
#Model 1: status ~ Differ + Extent
#Model 2: status ~ Age + Sex + Obstruct + Differ + Extent
# Resid. Df Resid. Dev Df Deviance Pr(>Chi)
#1 1806 2459.2
#2 1803 2456.0 3 3.2095 0.3604
根据AIC第二个模型较第一个模型优良,所以我们利用第二个模型来进行预测,构造一个新的数据集,并进行预测,如下:
####predict Differ + Extent,
newdata <- data.frame(Age=mean(mycolon$Age),
Sex=factor(c("Female", "Male")),
Obstruct=factor(c(0,1)),
Differ=factor(1:3),
Extent=factor(1:4)
)
newdata <- data.frame(
Differ=rep(factor(1:3),each =4),
Extent=factor(1:4)
)
newdata
Differ Extent
1 1 1
2 1 2
3 1 3
4 1 4
5 2 1
6 2 2
7 2 3
8 2 4
9 3 1
10 3 2
11 3 3
12 3 4
newdata$prob <- predict(fit.reduced, newdata=newdata, type="response")
newdata
Differ Extent prob
1 1 1 0.2134350
2 1 2 0.3269006
3 1 3 0.5001318
4 1 4 0.6223619
5 2 1 0.2135137
6 2 2 0.3270037
7 2 3 0.5002489
8 2 4 0.6224720
9 3 1 0.2902202
10 3 2 0.4225756
11 3 3 0.6012210
12 3 4 0.7129210
再来看下怎样查看模型中的各各参数:
- 查看各变量系数
coefficients(fit.full)
(Intercept) Age SexMale Obstruct1 Differ2 Differ3 Extent2 Extent3 Extent4
-1.178450077 -0.002182244 -0.043452048 0.190504495 0.008927713 0.413460103 0.580585812 1.285277260 1.798638342
- 查看各变量的95%置信区间
confint(fit.full)
Waiting for profiling to be done...
2.5 % 97.5 %
(Intercept) -2.12710018 -0.302055807
Age -0.01003899 0.005664344
SexMale -0.23101902 0.144069671
Obstruct1 -0.04766881 0.429623939
Differ2 -0.30483101 0.323993260
Differ3 0.03909403 0.789812640
Extent2 -0.18547118 1.433840932
Extent3 0.57195375 2.097973406
Extent4 0.95034348 2.725634614
- 查看各系数的OR值
exp(coefficients(fit.full))
(Intercept) Age SexMale Obstruct1 Differ2 Differ3 Extent2 Extent3 Extent4
0.3077554 0.9978201 0.9574785 1.2098598 1.0089677 1.5120406 1.7870850 3.6156703 6.0414155
- 查看系数OR值的95%置信区间
exp(confint(fit.full))
Waiting for profiling to be done...
2.5 % 97.5 %
(Intercept) 0.1191824 0.7392968
Age 0.9900112 1.0056804
SexMale 0.7937244 1.1549646
Obstruct1 0.9534495 1.5366795
Differ2 0.7372480 1.3826380
Differ3 1.0398683 2.2029836
Extent2 0.8307128 4.1947802
Extent3 1.7717252 8.1496372
Extent4 2.5865979 15.2660989
-
自动绘制logistics回归表格
通过各种参数自动输出 logistics 回归的结果,从上面可以看到,我们求变量的OR值,及5%置信区间需要分几步去做,如果需要汇总在一块工作量也会较大,但我们可以一键输出结果,非常放便,这需要加载一个 R 包 epiDisplay,一行命令搞定所有,如下:
install.packages("epiDisplay")
library(epiDisplay)
logistic.display(fit.full,crude.p.value = T,crude = T,decimal = T)
#####表格内容
Logistic regression predicting status
crude OR(95%CI) crude P value adj. OR(95%CI) P(Wald's test) P(LR-test)
Age (cont. var.) 0.9967 (0.9891,1.0044) 0.4 0.9978 (0.99,1.0057) 0.59 0.59
Sex: Male vs Female 1 (0.8,1.1) 0.61 1 (0.8,1.2) 0.65 0.65
Obstruct: 1 vs 0 1.3 (1,1.6) 0.04 1.2 (1,1.5) 0.12 0.12
Differ: ref.=1 0.01
2 1.1 (0.8,1.5) 0.64 1.009 (0.7371,1.3812) 0.96
3 1.7 (1.1,2.4) 0.01 1.5 (1,2.2) 0.03
Extent: ref.=1 < 0.001
2 1.8 (0.8,3.9) 0.16 1.8 (0.8,4) 0.16
3 3.7 (1.7,7.8) < 0.001 3.6 (1.7,7.7) < 0.001
4 6.2 (2.6,14.7) < 0.001 6 (2.5,14.6) < 0.001
Log-likelihood = -1227.988
No. of observations = 1812
AIC value = 2473.976
- 模型可视化
表格已经准备完成,下面我们就看下如何展示了,这里推荐一个 R 包 forestmodel 可以基于回归模型的结果绘制森林图,这个回归结果包括逻辑回归和Cox回归模型。
-
首先这个包支持ggplot2的主题,也就是theme_grey()、theme_bw()等;
-
可以通过panels参数调整图形中变量字体样式、粗细、各列宽度等;
-
上面的变量与每一个水平是没分开的,在同一线上,可以设置factor_separate_line参数来使其不在同一线上。
#install.packages("forestmodel") #安装和加载R包
library(forestmodel)
forest_model(
model,
panels = default_forest_panels(model, factor_separate_line = factor_separate_line),
covariates = NULL,
exponentiate = NULL,
funcs = NULL,
factor_separate_line = FALSE,
format_options = forest_model_format_options(),
theme = theme_forest(),
limits = NULL,
breaks = NULL,
return_data = FALSE,
recalculate_width = TRUE,
recalculate_height = TRUE,
model_list = NULL,
merge_models = FALSE,
exclude_infinite_cis = TRUE
)
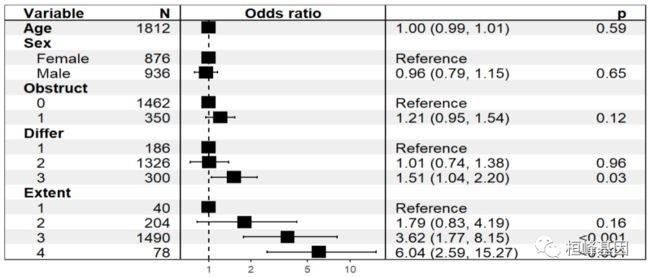
再来看我们构建模型的结果展示,如下:
forest_model(fit.full,
theme = theme_forest(),
factor_separate_line=TRUE
)
Reference:
-
Hosmer, D. & Lemeshow, S. (2000). Applied Logistic Regression (Second Edition). New York: John Wiley & Sons, Inc.
-
Long, J. Scott (1997). Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications.
桓峰基因
生物信息基础知识学习:R语言学习,perl基础编程,linux系统命令,Python遇见更好的你
25篇原创内容
公众号