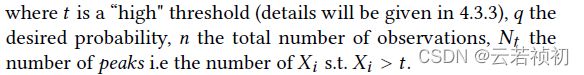基于极值理论的单变量时间序列流式异常检测算法SPOT/DSPOT

论文标题：“Anomaly Detection in Streams with Extreme Value Theory”

GitHub - Amossys-team/SPOT: SPOT algorithm implementation (with variants)https://github.com/Amossys-team/SPOT

算法简介

        SPOT是基于极值理论的流式数据异常检测算法。可用于单变量的流式数据异常检测，但是更常用于自动设置阈值（如OmniAnomaly就用该算法给异常分数设置阈值）。该算法通过拟合极值分布来计算指定概率下的极值，该极值被认为是判定异常的阈值。

        该算法的优势主要在于：（1）无需对数据分布做出假设（如3Sigma模型的前提条件是数据符合高斯分布），因此算法更鲁棒，更适用于不断变化的流式数据。（2）阈值的自动调整，该算法能根据数据的变化自动调整阈值，无需手工设置。（3）原理简单易于实现，速度尚可（FluxEV算法基于SPOT进行了改进，速度有明显提升）（4）biSPOT和bidSPOT能够同时对异常大和异常小的值进行检测。

        该算法的局限有：（1）仅适用于单变量的时间序列，不支持多变量。（2）对Concept Drift的适应能力有限，尽管DSPOT能够cover部分Concept Drift的情况，比起SPOT的适应能力好很多，但仍然很难适应复杂的产线环境。（3）算法初始化时需要用正常数据。（4）算法仍然有一些超参需要调节。

 

背景知识：极值理论

        极值的概念：

         极值zq要满足的条件是对于观察样本，大于它的概率小于q，q通常为一个很小的概率。这种极值为极大值，可作为异常大检测的阈值。

        极值理论（EVT）认为虽然不同的事物本身符合不同的数据分布，但是不同事物的极端事件满足相同的分布，这个分布称为极值分布。而SPOT算法应用的是EVT第二理论，它认为极值相对于一个阈值超出的部分满足一种分布叫GPD：

         GPD该数据分布模型有两个参数，γ和δ，这两个参数可以通过极大似然估计来获得。在SPOT算法中，t是一个固定值，为初始化数据的98%分位数，所有高于t的值且非异常的值被叫做peaks。SPOT算法认为这些peaks满足上述的GPD分布。一旦求出了这些peaks就可以用极大似然估计来确定GPD的两个参数。确定了GPD模型，就不难找到概率q对应的极值zq，而该极值即判断异常大的阈值。

 

SPOT算法原理

        SPOT的步骤可以分为两步：

        （1）calibration，或者叫初始化。根据已有的数据计算t和阈值Zq。

        （2）流式更新阈值Zq，并把它当做决策边界判断异常。大于Zq的为异常，报出去；在t和zq之间的为peaks，用于更新GPD模型和Zq；小于t的为正常数据，不做处理

        

下面先介绍初始化步骤，再介绍SPOT算法的整个流程。

初始化

        目标：We have n observations X1, . . .Xn, and we have fixed a risk q. The goal is to compute a first threshold zq verifying P(X > zq) < q.

        做法： 设置一个较高的阈值t，超过t的都认为是peak，从而得到peaks set Yt，根据Yt拟合GPD，得到GPD的参数，然后就可以计算出阈值Zq。

 流式异常检测

        首先取前n个值做初始化得到t和阈值zq。

        如果新来的值大于zq，那就被认为是异常值，放到异常集合A中（A作为最终的结果输出），异常值不更新模型。如果新来的值大于t，即real peak case，那就更新模型（GPD模型），得到新的zq。否则就是normal case。

        同样的方法也可以去检测极小的异常。

DSPOT算法原理

SPOT的问题： 前提条件是数据分布不随时间变化。无法适应Concept Drift。

DSPOT的做法：用与局部平均M的相对值（上图的蓝和红）来代替原先的绝对值进行SPOT。该算法认为这个相对值的分布不随时间变化，即这个相对值满足SPOT的前提条件。

相对值的计算方式：

 其中Mi is a moving average，它是最近的d个正常值（包含normal 和peak)的均值。 d是一个超参（窗长）

 DSPOT算法流程

        先取前d个数计算M（初始化M）

        再取n个数计算相对值X', 拟合模型得到初始阈值zq（初始化阈值zq）

        流式更新模型：如果新来的相对值大于zq，判断为异常，不更新模型（特指极值分布模型），不更新M值。如果新来的相对值是peak（大于t），更新模型，更新M；否则，只更新M，不更新模型。