【笔记】【机器学习基础】主成分分析

主成分分析

主成分分析（PCA）是一种旋转数据集的方法，旋转后的特征在统计上不相关。
(1)用PCA做数据变换

mglearn.plots.plot_pca_illustration()

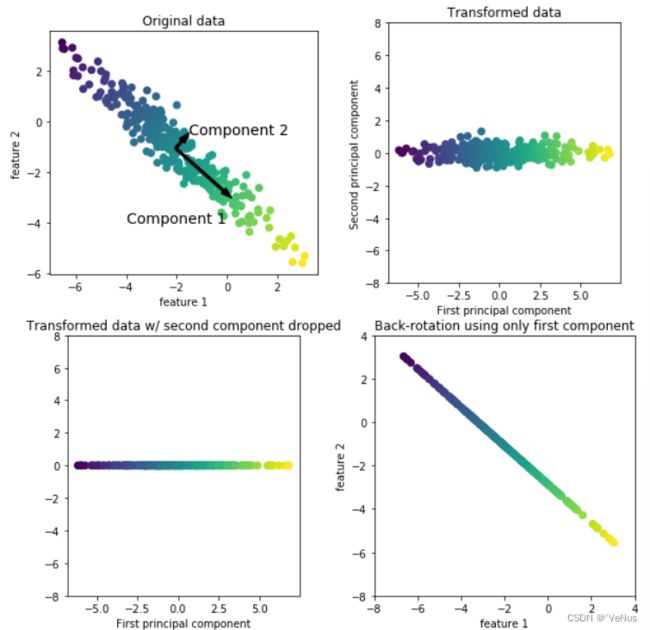
图1：在原始数据点集中，找到方差最大的方向，标记为成分1。这是包含信息最多的方向（或向量）。找到与成分1正交（成直角）且包含最多信息的方向，标记为成分2。其找到的方向即为主成分

图2：将数据旋转，使第一主成分与X轴平行，旋转前从数据中减去平均值，使得变换后的数据以0为中心。

图3：仅保留一部分主成分进行降维。

图4：反向旋转并将平均值重新加到数据中。

1、将PCA用于cancer数据集并可视化

（1）计算每个类别的特征直方图

fig, axes = plt.subplots(15, 2, figsize=(10, 20))
malignant = cancer.data[cancer.target == 0]
benign = cancer.data[cancer.target == 1]

ax = axes.ravel()

for i in range(30):
    _, bins = np.histogram(cancer.data[:, i], bins=50)
    ax[i].hist(malignant[:, i], bins=bins, color=mglearn.cm3(0), alpha=.5)
    ax[i].hist(benign[:, i], bins=bins, color=mglearn.cm3(2), alpha=.5)
    ax[i].set_title(cancer.feature_names[i])
    ax[i].set_yticks(())
ax[0].set_xlabel("Feature magnitude")
ax[0].set_ylabel("Frequency")
ax[0].legend(["malignant", "benign"], loc="best")
fig.tight_layout()

计算了具有某一特征的数据点在特定范围内的出现频率。
但是无法展示变量之间的相互作用，以及相互作用与类别的关系，通过PCA获取主要的相互作用。

（2）利用StandardScaler缩放数据

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()

scaler = StandardScaler()
scaler.fit(cancer.data)
X_scaled = scaler.transform(cancer.data)

（3）在创建PCA对象前指定保留的主成分个数

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X_scaled)

X_pca = pca.transform(X_scaled)
print("Original shape: {}".format(str(X_scaled.shape)))
print("Reduced shape: {}".format(str(X_pca.shape)))

Original shape: (569, 30)
Reduced shape: (569, 2)

（4）利用前两个主成分绘制二维散点图

plt.figure(figsize=(8, 8))
mglearn.discrete_scatter(X_pca[:, 0], X_pca[:, 1], cancer.target)
plt.legend(cancer.target_names, loc="best")
plt.gca().set_aspect("equal")
plt.xlabel("First principal component")
plt.ylabel("Second principal component")

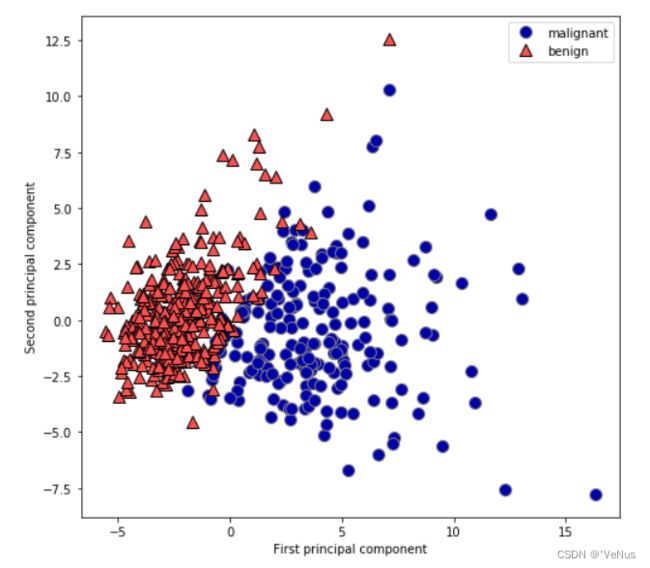
PCA没有用到类别信息，只是观察数据中的相关性。但是从图中看出即使是线性分类器也能很好区分这两个类别
PCA缺点：不容易对图中的两个轴进行解释。

（5）

print("PCA component shape: {}".format(pca.components_.shape))

PCA component shape: (2, 30)
主成分保存在components_属性中

print("PCA components:\n{}".format(pca.components_))

PCA components:
[[ 0.219 0.104 0.228 0.221 0.143 0.239 0.258 0.261 0.138 0.064
0.206 0.017 0.211 0.203 0.015 0.17 0.154 0.183 0.042 0.103
0.228 0.104 0.237 0.225 0.128 0.21 0.229 0.251 0.123 0.132]
[-0.234 -0.06 -0.215 -0.231 0.186 0.152 0.06 -0.035 0.19 0.367
-0.106 0.09 -0.089 -0.152 0.204 0.233 0.197 0.13 0.184 0.28
-0.22 -0.045 -0.2 -0.219 0.172 0.144 0.098 -0.008 0.142 0.275]]
components_中每一行对应一个主成分，按重要性排序，列对应PCA的原始特征属性

（6）前两个主成分的热图

plt.matshow(pca.components_, cmap='viridis')
plt.yticks([0, 1], ["First component", "Second component"])
plt.colorbar()
plt.xticks(range(len(cancer.feature_names)),
           cancer.feature_names, rotation=60, ha='left')
plt.xlabel("Feature")
plt.ylabel("Principal components")

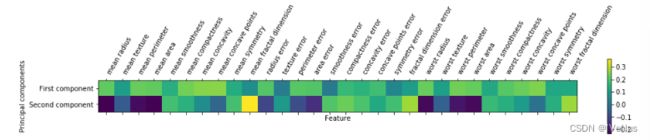
第一个主成分中，所有特征的符号相同，说明特征之间存在普遍的相关性。第二个主成分中符号有正有负，这种混合使得解释坐标轴很困难

2、特征提取的特征脸

思想：可以找到一种数据表示，比给定的原始数据更适合于分析。

（1）数据集（Wild数据集中的人脸图像）

from sklearn.datasets import fetch_lfw_people
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape

fig, axes = plt.subplots(2, 5, figsize=(15, 8),
                         subplot_kw={'xticks': (), 'yticks': ()})
for target, image, ax in zip(people.target, people.images, axes.ravel()):
    ax.imshow(image)
    ax.set_title(people.target_names[target])

这个数据集有3023张图片，每张87*65像素，分别属于62个人

print("people.images.shape: {}".format(people.images.shape))
print("Number of classes: {}".format(len(people.target_names)))

people.images.shape: (3023, 87, 65)
Number of classes: 62
数据集偏斜
比如：

counts = np.bincount(people.target)

for i, (count, name) in enumerate(zip(counts, people.target_names)):
    print("{0:25} {1:3}".format(name, count), end='   ')
    if (i + 1) % 3 == 0:
        print()

（2）降低数据集偏斜，每个最多取50张

mask = np.zeros(people.target.shape, dtype=np.bool)
for target in np.unique(people.target):
    mask[np.where(people.target == target)[0][:50]] = 1
    
X_people = people.data[mask]
y_people = people.target[mask]

X_people = X_people / 255.

（3）构建分类器进行人脸识别
构建一个分类器，每个人是一个类别，但是类别的训练数据不足，同一个人图像很少，而且难添加新人物
使用单一近邻分类器，原则上能处理内个类别只有一个训练样例的情况

from sklearn.neighbors import KNeighborsClassifier

X_train, X_test, y_train, y_test = train_test_split(
    X_people, y_people, stratify=y_people, random_state=0)

knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
print("Test set score of 1-nn: {:.2f}".format(knn.score(X_test, y_test)))

Test set score of 1-nn: 0.23
精度不高

（4）使用PCA提高精度
精度较低，因为计算原始像素空间中的距离时，如果使用像素距离，将人脸右移一个像素将会发生巨大变化，得到一个完全不同的表示。
使用沿着主成分方向的距离可以提高精度，启用PCA 的白化选项

mglearn.plots.plot_pca_whitening()

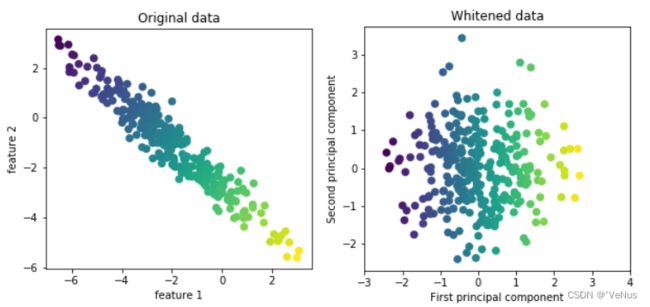
拟合PCA对象，取前100个主成分，对训练数据和测试数据进行变换

pca = PCA(n_components=100, whiten=True, random_state=0).fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)

print("X_train_pca.shape: {}".format(X_train_pca.shape))

X_train_pca.shape: (1547, 100)

使用分类器进行图像分类：

knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train_pca, y_train)
print("Test set accuracy: {:.2f}".format(knn.score(X_test_pca, y_test)))

Test set accuracy: 0.31
精度有了显著的提高，说明主成分可能提供了一种更好地数据表示

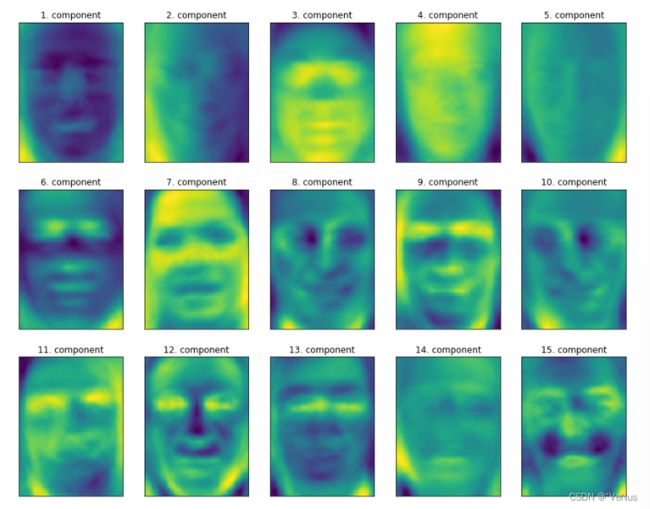
（5）主成分可视化

print("pca.components_.shape: {}".format(pca.components_.shape))

pca.components_.shape: (100, 5655)


fig, axes = plt.subplots(3, 5, figsize=(15, 12),
                         subplot_kw={'xticks': (), 'yticks': ()})
for i, (component, ax) in enumerate(zip(pca.components_, axes.ravel())):
    ax.imshow(component.reshape(image_shape),
              cmap='viridis')
    ax.set_title("{}. component".format((i + 1)))

第一个主成分编码人脸与背景的对比，第二个编码人左右脸的明暗程度差异等，都与人感知人脸的方式不同。