TensorFlow实现梯度下降法
TensorFlow实现一元线性回归
第1步导入需要的库、加载数据样本
import tensorflow as tf
import numpy as np
# 第1步导入需要的库、加载数据样本
x = np.array([137.97, 104.50, 100.00, 124.32, 79.20, 99.00, 124.00, 114.00,
106.69, 138.05, 53.75, 46.91, 68.00, 63.02, 81.26, 86.21])
y = np.array([145.00, 110.00, 93.00, 116.00, 65.32, 104.00, 118.00, 91.00,
62.00, 133.00, 51.00, 45.00, 78.50, 69.65, 75.69, 95.30])
第2步设置超参数
# 第2步设置超参数
learn_rate = 0.0001
iter = 10
display_step = 1
第3步给模型参数w和b设置初值
为了能够被梯度带自动监视,这里将w和b 封装为Variable对象
# 第3步给模型参数w和b设置初值
np.random.seed(612)
w = tf.Variable(np.random.rand())
b = tf.Variable(np.random.rand())
第4步训练模型
把线性模型和损失函数的表达式写在梯度带的with语句中,然后把手工计算梯度的代码改为使用梯度带对象的gradient方法自动获取梯度,接下来使用迭代公式更新模型参数给valuable对象,赋值需要使用它的assign方法,这里使用assign_sub方法实现减法运算。
# 第4步训练模型
mse = []
for i in range(0, iter + 1):
with tf.GradientTape() as tape:
pred = w * x + b
Loss = tf.reduce_mean(tf.square(y - pred)) / 2
mse.append(Loss)
dL_dw, dL_db = tape.gradient(Loss, [w, b])
w.assign_sub(learn_rate * dL_dw)
b.assign_sub(learn_rate * dL_db)
if i % display_step == 0:
print("i: %i, Loss: %f, w: %f, b: %f" % (i, Loss, w.numpy(), b.numpy()))
这是运行结果
i: 0, Loss: 3237.576416, w: 0.932160, b: 0.503558
i: 1, Loss: 88.893135, w: 0.941856, b: 0.503690
i: 2, Loss: 88.417160, w: 0.941975, b: 0.503729
i: 3, Loss: 88.417068, w: 0.941976, b: 0.503767
i: 4, Loss: 88.417061, w: 0.941976, b: 0.503806
i: 5, Loss: 88.417053, w: 0.941976, b: 0.503844
i: 6, Loss: 88.417015, w: 0.941975, b: 0.503882
i: 7, Loss: 88.417007, w: 0.941975, b: 0.503920
i: 8, Loss: 88.416992, w: 0.941975, b: 0.503958
i: 9, Loss: 88.416992, w: 0.941974, b: 0.503997
i: 10, Loss: 88.416962, w: 0.941974, b: 0.504035
可以看到和numpy方法得到的结果,非常的接近。这些数值不完全相同,是因为numpy默认的浮点数数据类型是64位的,而tensorflow默认为32位浮点数
虽然使用numpy函数生成浮点数,但是因为参数为空,返回的是一个数字,它是Python的float类型,它的float在创建valuable对象时,当参数是一个浮点数数字时,默认采用32位浮点数。
如果在这里指定使用64位浮点数,就可以得到和安排程序完全相同的结果
TensorFlow实现多元线性回归
第1步导入需要的库、加载数据样本
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
# 加载样本数据
area = np.array([137.97, 104.50, 100.00, 124.32, 79.20, 99.00, 124.00, 114.00,
106.69, 138.05, 53.75, 46.91, 68.00, 63.02, 81.26, 86.21])
room = np.array([3, 2, 2, 3, 1, 2, 3, 2, 2, 3, 1, 1, 1, 1, 2, 2])
price = np.array([145.00, 110.00, 93.00, 116.00, 65.32, 104.00, 118.00, 91.00,
62.00, 133.00, 51.00, 45.00, 78.50, 69.65, 75.69, 95.30])
num = len(area)
第2步数据处理
x0 = np.ones(num)
x1 = (area - area.min()) / (area.max() - area.min())
x2 = (room - room.min()) / (room.max() - room.min())
X = np.stack((x0, x1, x2), axis=1)
Y = price.reshape(-1, 1)
第3步设置超参数
learn_rate = 0.2
iter = 50
display_step = 10
前面这3步和numpy程序是完全一样的
第4步设置模型参数初始值
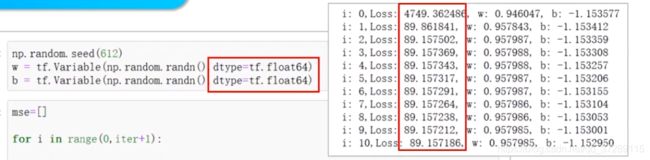
这里首先使用numpy函数生成随机数组,numpy默认采用64位浮点数,然后把它封装为tensorflow的Variable对象,由于参数是64位的numpy数组,所以所生成的Variable对象的数据类型也是64位浮点数,这个和我们之前介绍的创建探测张量是一样的。
一般来说建议大家在这里指定采用32位浮点数,在这个例子中,为了便于和numpy程序的结果进行比较,我们采用numpy默认的64位浮点数
np.random.seed(612)
W = tf.Variable(np.random.randn(3, 1))
第5步训练模型
首先把线性模型和损失函数的表达式写在梯度带对象的with语句中,然后自动求取梯度,这里w是一个形状为(3, 1)的二维数组。计算出的梯度也是一个形状为(3, 1)的二维数组。
下面使用梯度来更新所有的模型参数,可以看到实现多元线性回归方法和实现一元线性回归是完全一样的,只是模型中的x,w是多维数组的形式
mse = []
for i in range(0, iter + 1):
with tf.GradientTape() as tape:
PRED = tf.matmul(X, W)
Loss = 0.5 * tf.reduce_mean(tf.square(Y - PRED))
mse.append(Loss)
dl_dW = tape.gradient(Loss, W)
W.assign_sub(learn_rate*dl_dW)
if i % display_step == 0:
print("i: %i, Loss: %f" % (i, Loss))
这是运行的结果
i: 0, Loss: 4593.851656
i: 10, Loss: 85.480869
i: 20, Loss: 82.080953
i: 30, Loss: 81.408948
i: 40, Loss: 81.025841
i: 50, Loss: 80.803450
和前面numpy程序得到的结果是一样的,使用tensorflow实现梯度下降法,梯度带会自动计算损失函数的梯度,而不用我们去写代码,实现偏导数的计算过程