(三) 三维点云课程---RANSAC结合最小二乘求解点云的地面
三维点云课程—RANSAC结合最小二乘求解点云的地面
三维点云课程---RANSAC结合最小二乘求解点云的地面
- 三维点云课程---RANSAC结合最小二乘求解点云的地面
-
- 1.RANSAC的步骤
- 2.RANCAC的代码分析
-
- 2.1输入参数 τ , N \tau,N τ,N的分析
- 2.2 平面模型的创建
- 2.3统计内点的个数
- 2.4最小二乘优化
- 2.5提前终止RANSAC的迭代
- 3.RANSAC完整代码
1.RANSAC的步骤
- 1.从原始点中随机选择三个点,建立平面模型
- 2.求解平面模型,比如 a x + b y + c z + d = 0 ax+by+cz+d=0 ax+by+cz+d=0
- 3.其他点相对该平面的误差,误差表示为其他点相对该平面的距离 d i d_i di
- 4.统计内点的个数,点为内点的条件 d i < τ d_i<\tau di<τ,其中 τ \tau τ是人为设定的
- 5.重复1-4步的N次迭代,选择N次迭代中内点数最多的平面模型

2.RANCAC的代码分析
2.1输入参数 τ , N \tau,N τ,N的分析
关于 τ \tau τ的确定是通过实验得到的,其实也可以通过卡方分布得到,但是卡方分布的要求较多,实际中并不满足卡方的要求,大多数是通过实验得到的。
迭代次数N的确定
( 1 − ( 1 − e ) s ) N = 1 − p N = l o g ( 1 − p ) l o g ( 1 − ( 1 − e ) s ) (1-(1-e)^s)^N=1-p \\ N=\frac{log(1-p)}{log(1-(1-e)^s)} (1−(1−e)s)N=1−pN=log(1−(1−e)s)log(1−p)
其中参数如下
e:一个点是外点的概率,这个给一个大概的值就可以了
s:解出一个模型至少需要多少个数据点,平面的话s为3
N:迭代的次数
p:作N次迭代,至少能够取到一个好的sample(没有外点,只有内点)的概率,大多数设为0.9,0.99,当然0.99的迭 代次数要比0.9的要多。
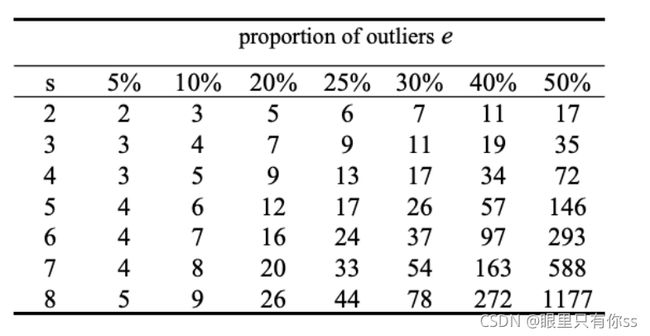
其中上述的图为p=0.99的结果。例如图中的1177表示为,当模型参数至少需要 s = 8 s=8 s=8个点,一个点是外点的概率是 e = 50 e=50% e=50, p = 0.99 p=0.99 p=0.99的情况下,迭代次数 N = 1177 N=1177 N=1177
#确认迭代次数
if math.log(1 - (1 - e) ** s) < sys.float_info.min:
N = N_regular
else:
N = math.log(1 - p) / math.log(1 - (1 - e) ** s)
2.2 平面模型的创建
ids = random.sample(range(0, t), 3)
p1, p2, p3 = X[ids]
# 判断是否共线
L = p1 - p2
R = p2 - p3
if 0 in L or 0 in R:
continue
else:
if L[0] / R[0] == L[1] / R[1] == L[2] / R[2]:
continue
# 计算平面参数
#参考A(x-x1)+B(y-y1)+C(z-z1)=0,代入(x2,y2,z2)和(x3,y3.z3)
a = (p2[1] - p1[1]) * (p3[2] - p1[2]) - (p2[2] - p1[2]) * (p3[1] - p1[1]);
b = (p2[2] - p1[2]) * (p3[0] - p1[0]) - (p2[0] - p1[0]) * (p3[2] - p1[2]);
c = (p2[0] - p1[0]) * (p3[1] - p1[1]) - (p2[1] - p1[1]) * (p3[0] - p1[0]);
d = 0 - (a * p1[0] + b * p1[1] + c * p1[2]);
其中平面模型的创建
设过 p 1 ( x 0 , y − y 0 , z 0 ) p_1(x_0,y-y_0,z_0) p1(x0,y−y0,z0)的平面方程为
A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_0)+B(y-y_0)+C(z-z_0)=0 A(x−x0)+B(y−y0)+C(z−z0)=0
因为 p 2 ( x 1 , y 1 , z 1 ) , p 3 ( x 2 , y 2 , z 2 ) p_2(x_1,y_1,z_1),p_3(x_2,y_2,z_2) p2(x1,y1,z1),p3(x2,y2,z2)都在这个平面上,那么
A ( x 1 − x 0 ) + B ( y 1 − y 0 ) + C ( z 1 − z 0 ) = 0 A ( x 2 − x 0 ) + B ( y 2 − y 0 ) + C ( z 2 − z 0 ) = 0 A(x_1-x_0)+B(y_1-y_0)+C(z_1-z_0)=0 \\ A(x_2-x_0)+B(y_2-y_0)+C(z_2-z_0)=0 A(x1−x0)+B(y1−y0)+C(z1−z0)=0A(x2−x0)+B(y2−y0)+C(z2−z0)=0
化成矩阵方程为
[ x − x 0 y − y 0 z − z 0 x − x 1 y − y 1 z − z 1 x − x 2 y − y 2 z − z 2 ] [ A B C ] = 0 \begin{bmatrix} {x - {x_0}}&{y - {y_0}}&{z - {z_0}}\\ {x - {x_1}}&{y - {y_1}}&{z - {z_1}}\\ {x - {x_2}}&{y - {y_2}}&{z - {z_2}} \end{bmatrix}\begin{bmatrix} A\\ B\\ C \end{bmatrix} = 0 ⎣⎡x−x0x−x1x−x2y−y0y−y1y−y2z−z0z−z1z−z2⎦⎤⎣⎡ABC⎦⎤=0
那么要使 [ A , B , C ] T [A,B,C]^T [A,B,C]T为非零解,那么
[ x − x 0 y − y 0 z − z 0 x − x 1 y − y 1 z − z 1 x − x 2 y − y 2 z − z 2 ] = 0 \begin{bmatrix} {x - {x_0}}&{y - {y_0}}&{z - {z_0}}\\ {x - {x_1}}&{y - {y_1}}&{z - {z_1}}\\ {x - {x_2}}&{y - {y_2}}&{z - {z_2}} \end{bmatrix}=0 ⎣⎡x−x0x−x1x−x2y−y0y−y1y−y2z−z0z−z1z−z2⎦⎤=0
进而推导出代码的样子。
2.3统计内点的个数
dis = abs(a * X[:, 0] + b * X[:, 1] + c * X[:, 2] + d) / (a**2 + b**2 + c**2) ** 0.5
idset = []
for i, d in enumerate(dis):
if d < tao:
idset.append(i)
核心公式为点到平面的距离
d i s t = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 dist=\frac{{|A{x_0} + B{y_0} + C{z_0} + D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }} dist=A2+B2+C2∣Ax0+By0+Cz0+D∣
其中代码中的tao就是认为设置的 τ \tau τ
2.4最小二乘优化
其实上面的一些代码分析,RANSAC算法就已经结束了,但是RANSAC得到的结果不一定准确,那么通过最小二乘的方法对RANSAC算法进一步优化
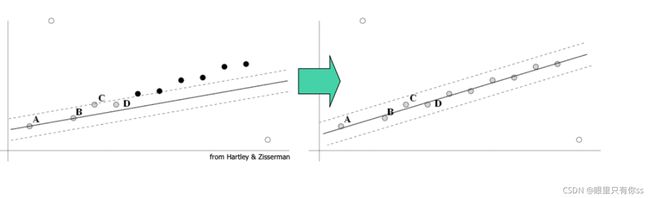
上面左图是通过RANSAC得到的内点,右图是通过最小二乘进一步对得到的内点进行优化,使得结果更准确
def PlaneLeastSquare(X: np.ndarray):
# z=ax+by+c,return a,b,c
A = X.copy()
b = np.expand_dims(X[:, 2], axis=1) #(M,)tuple类型变成 M*1的array类型
A[:, 2] = 1
# 通过X=(AT*A)-1*AT*b直接求解
A_T = A.T
A1 = np.dot(A_T, A)
A2 = np.linalg.inv(A1)
A3 = np.dot(A2, A_T)
x = np.dot(A3, b)
return x
其中X就是RANSAC得到的内点数,在这里优化的平面模型是 a x + b y + c = z ax+by+c=z ax+by+c=z,化成矩阵如下
A = [ x 0 y 0 1 x 1 y 1 1 . . . . . . . . . x n y n 1 ] x = [ a b c ] b = [ z 0 z 1 . . . z n ] A =\begin{bmatrix} {{x_0}}&{{y_0}}&1\\ {{x_1}}&{{y_1}}&1\\ {...}&{...}&{...}\\ {{x_n}}&{{y_n}}&1 \end{bmatrix} \\ x =\begin{bmatrix} a\\ b\\ c \end{bmatrix}\\ b =\begin{bmatrix} {{z_0}}\\ {{z_1}}\\ {...}\\ {{z_n}} \end{bmatrix} \\ A=⎣⎢⎢⎡x0x1...xny0y1...yn11...1⎦⎥⎥⎤x=⎣⎡abc⎦⎤b=⎣⎢⎢⎡z0z1...zn⎦⎥⎥⎤
那么就是经典的最小二乘问题 A x = b Ax=b Ax=b, x x x的解析解为 x = ( A T A ) − 1 A b x=(A^TA)^{-1}Ab x=(ATA)−1Ab,文中的代码也是这样操作的。
2.5提前终止RANSAC的迭代
if len(idset) > t * (1 - e):
break
其中idset是RANSAC得到的内点集合,当某次RANSAC算法算出的inliner数大于等于(1-e)乘以原始点云数,RANSAC算法就可以终止了。即
T ≥ ( 1 − e ) × t o t a l _ n u m _ o f _ d a t a _ p o i n t s T \ge (1-e) \times total\_num\_of\_data\_points T≥(1−e)×total_num_of_data_points
代码也是上述的复现
3.RANSAC完整代码
# 文件功能:
# 1. 从数据集中加载点云数据
# 2. 从点云数据中滤除地面点云
# 3. 从剩余的点云中提取聚类
import numpy as np
import os
import struct
from sklearn import cluster, datasets, mixture
from mpl_toolkits.mplot3d import Axes3D
import random
import open3d
import math
import sys
from scipy.spatial import KDTree
import sklearn.cluster
#读取bin文件获取三维数据
def read_velodyne_bin(path):
pc_list = []
with open(path, 'rb') as f:
content = f.read()
pc_iter = struct.iter_unpack('ffff', content)
for idx, point in enumerate(pc_iter):
pc_list.append([point[0], point[1], point[2]])
return np.asarray(pc_list, dtype=np.float32)
#最小二乘函数,优化提取的平面
#输入参数:待优化的点云数
#输出参数:最小二乘拟合的平面参数(a,b,c)
def PlaneLeastSquare(X: np.ndarray):
# z=ax+by+c,return a,b,c
A = X.copy()
b = np.expand_dims(X[:, 2], axis=1) #(M,)tuple类型变成 M*1的array类型
A[:, 2] = 1
# 通过X=(AT*A)-1*AT*b直接求解
A_T = A.T
A1 = np.dot(A_T, A)
A2 = np.linalg.inv(A1)
A3 = np.dot(A2, A_T)
x = np.dot(A3, b)
return x
#RANSAC算法,提取平面
#输入参数 X:输入的点云数据,tao:外点距离平面的距离因子,e:一个点是外点的概率,N_regular:默认迭代次数
#输出参数:内点,外点,平面的四参数(a,b,c,d)
def PlaneRANSAC(X: np.ndarray, tao: float, e=0.4, N_regular=100):
# return plane ids
t = X.shape[0]
s = X.shape[1]
count = 0
p = 0.99
dic = {}
#确认迭代次数
if math.log(1 - (1 - e) ** s) < sys.float_info.min:
N = N_regular
else:
N = math.log(1 - p) / math.log(1 - (1 - e) ** s)
# 开始迭代
while count < N:
ids = random.sample(range(0, t), 3)
p1, p2, p3 = X[ids]
# 判断是否共线
L = p1 - p2
R = p2 - p3
if 0 in L or 0 in R:
continue
else:
if L[0] / R[0] == L[1] / R[1] == L[2] / R[2]:
continue
# 计算平面参数
#参考A(x-x1)+B(y-y1)+C(z-z1)=0,代入(x2,y2,z2)和(x3,y3.z3)
a = (p2[1] - p1[1]) * (p3[2] - p1[2]) - (p2[2] - p1[2]) * (p3[1] - p1[1]);
b = (p2[2] - p1[2]) * (p3[0] - p1[0]) - (p2[0] - p1[0]) * (p3[2] - p1[2]);
c = (p2[0] - p1[0]) * (p3[1] - p1[1]) - (p2[1] - p1[1]) * (p3[0] - p1[0]);
d = 0 - (a * p1[0] + b * p1[1] + c * p1[2]);
dis = abs(a*X[:, 0] + b*X[:, 1]+ c*X[:, 2]+d) / (a**2 + b**2 + c** 2) ** 0.5
idset = []
for i, d in enumerate(dis):
if d < tao:
idset.append(i)
# 再使用最小二乘法,得到更加准确的a,b,c,d
p = PlaneLeastSquare(X[idset])
a, b, c, d = p[0], p[1], -1, p[2]
dic[len(idset)] = [a, b, c, d]
if len(idset) > t * (1 - e):
break
count += 1
parm = dic[max(dic.keys())]
a, b, c, d = parm
dis = abs(a*X[:, 0] + b*X[:, 1]+ c*X[:, 2]+d) / (a**2 + b**2 + c** 2) ** 0.5
idset = []
odset = []
for i, d in enumerate(dis):
if d < tao:
idset.append(i)
else:
odset.append(i)
print("地面的内点数,外点数:",len(idset),len(odset))
return np.array(idset),np.array(odset),a,b,c,d
#点云旋转--显示
def rotate_view(vis):
ctr = vis.get_view_control()
ctr.rotate(0.0, 10.0)
return False
if __name__ == '__main__':
##原始数据的加载
#读取数据
origin_points = read_velodyne_bin("000000.bin")
#建立点云对象
pcd=open3d.geometry.PointCloud()
#加载点云数据
pcd.points=open3d.utility.Vector3dVector(origin_points)
#改变点云颜色
c=[0,0,0]
cs=np.tile(c,(origin_points.shape[0],1))
pcd.colors=open3d.utility.Vector3dVector(cs)
#添加坐标系
FOR1 = open3d.geometry.TriangleMesh.create_coordinate_frame(size=5, origin=[0, 0, 0])
#显示点云
open3d.visualization.draw_geometries([FOR1,pcd])
print("原始数据的个数、维数:",origin_points.shape[0],origin_points.shape[1])
##通过RANSAC算法获得点云的地面
planeids,othersids,pa,pb,pc,pd=PlaneRANSAC(origin_points,0.35)
planedata = origin_points[planeids]
planepcd = open3d.geometry.PointCloud()
planepcd.points = open3d.utility.Vector3dVector(planedata)
c = [0, 0, 255]
cs = np.tile(c, (planedata.shape[0], 1))
planepcd.colors = open3d.utility.Vector3dVector(cs)
otherdata = origin_points[othersids]
otherpcd = open3d.geometry.PointCloud()
otherpcd.points = open3d.utility.Vector3dVector(otherdata)
c = [255, 0, 0]
cs = np.tile(c, (otherdata.shape[0], 1))
otherpcd.colors = open3d.utility.Vector3dVector(cs)
open3d.visualization.draw_geometries([planepcd, otherpcd])
print("地面方程为a,b,c,d:",pa[0],pb[0],pc,pd)
##sklearn库下的DBSCAN进行聚类
Css = sklearn.cluster.DBSCAN(eps=0.50, min_samples=4).fit(otherdata)
ypred = np.array(Css.labels_)
print("聚类的个数:",ypred.shape[0])
ddraw = []
colorset = [[222, 0, 0], [0, 224, 0], [0, 255, 255], [222, 244, 0], [255, 0, 255], [128, 0, 0]]
for cluuus in set(ypred):
kaka = np.where(ypred == cluuus)
ppk = open3d.geometry.PointCloud()
ppk.points = open3d.utility.Vector3dVector(otherdata[kaka])
if len(ppk.points)<10:
continue
c = colorset[cluuus % 3]
if cluuus == -1:
c = [0, 0, 0]
cs = np.tile(c, (otherdata[kaka].shape[0], 1))
ppk.colors = open3d.utility.Vector3dVector(cs)
ddraw.append(ppk)
ddraw.append(planepcd)
open3d.visualization.draw_geometries(ddraw)
#点云绕着轴旋转
#open3d.visualization.draw_geometries_with_animation_callback(ddraw,rotate_view)
注意:最后一行代码打开,会发现神奇的东西哦
数据集取自KITTI的激光雷达数据,就其中的两个数据集进行仿真,效果如下
KITTI数据集比较大,需要完全的KITTI数据集,加我QQ:2822908208
000000.bin密码7875
原始数据

RANSAC提取地面

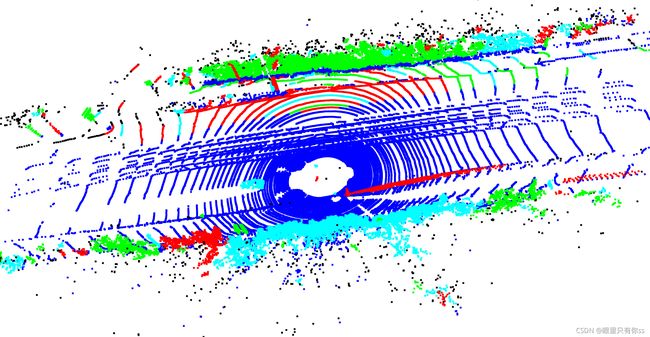
DBSCAN进行聚类

000001.bin密码7875
原始数据
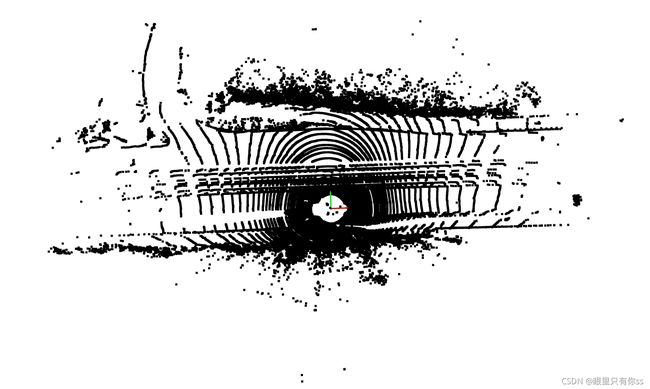
RANSAC提取地面
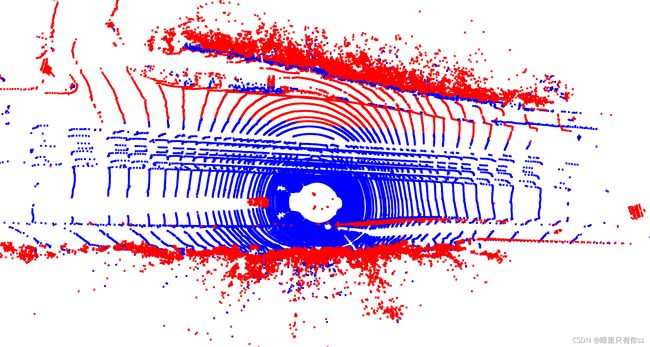
DBSCAN进行聚类