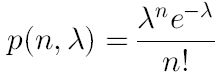ransac java_RANSAC与其改进

1. 经典RANSAC

由Fischer和Bolles在1981年的文章[1]中首先提出，简要的说经典RANSAC的目标是不断尝试不同的目标空间参数，使得目标函数 C最大化的过程。这个过程是随机(Random)、数据驱动(data-driven)的过程。通过反复的随机选择数据集的子空间来产生一个模型估计，然后利用估计出来的模型，使用数据集剩余的点进行测试，获得一个得分，最终返回一个得分最高的模型估计作为整个数据集的模型。

1.1 目标函数

在经典的RANSAC流程中，目标函数C可以被看作：在第k次迭代过程中，在当前变换参数

作用下，数据集

中满足变换参数的点的个数，也就是在当前变换条件下类内点的个数，而RANSAC就是最大化 C的的过程。而判断当前某个点是否为类内需要一个阈值t。

1.2 子集大小

在迭代的过程中，当前变换参数 θ 的计算需要

中的一个子集 I来计算，RANSAC是一个随机从

中采样一个子集，然后对参数“估计-确认”的循环。每一个子集应是一个大小为m的最小采样。所谓最小采样，就是m的大小刚好满足计算θ的个数即可。

1.3 循环终止条件

按照参考文献[1]中的说明，在置信度为

的条件下，在循环过程中，至少有一次采样，使得采样出的m个点均为类内点，这样才能保证在循环的过程中，至少有一次采样能取得目标函数的最大值。因此，采样次数k应该满足以下条件：

这里除了置信度

外，m为子集大小，ε为类内点在

中的比例，其中置信度一般设置为[0.95, 0.99]的范围内。然而在一般情况下，ε 显然是未知的，因此 ε 可以取最坏条件下类内点的比例，或者在初始状态下设置为最坏条件下的比例，然后随着迭代次数，不断更新为当前最大的类内点比例。

另外一种循环终止条件可以将选取的子集看做为“全部是类内点”或“不全部是类内点”这两种结果的二项分布，而前者的概率为

。对于 p足够小的情况下，可以将其看作为一种泊松分布，因此，在 k次循环中，有 n个“子集全部是类内点”的概率可以表达为：

λ表示在 k次循环中，“子集全都是类内点”的选取次数的期望。例如在RANSAC中，我们希望在这k次循环中所选子集“没有一个全是类内点”的概率小于某个置信度，即：

，以置信度为95%为例，λ约等于3，表示在95%置信度下，在 k次循环中，平局可以选到3次“好”的子集。

1.4 判断阈值的选取

阈值 t是判断在当前的获得的参数 θ下，

中某一点是类内点还是类外点的判断依据。在这里，假定类外点是高斯白噪声，其均值为0，方差为 σ，误差的残差(residuals)符合 n维的卡方分布(chi-square)。而误差阈值的选取即可以按照以下的公式计算[2]。

α为置信概率，若 α=0.95，那么一个真实的类内点被误分类为类外点的概率为5%。

经典RANSAC算法的流程如下图所示：

2. Universal-RANSAC

经典RANSAC有以下三个主要的局限性：

(1) 效率：经典方法效率与子集大小、类内点比例以及数据集大小有关，因此在某些场景下效率较低。

(2) 精度：经典方法计算参数时选取最小子集是从效率的角度考虑，往往得到的是非最佳参数，在应用产参数 之前还需要再经过细化处理。

(3) 退化：经典方法的目标函数求取最大化的过程基于一个假设：“选取的最小子集中如果有类外点，那么在这种情况下估计的参数获得的目标函数(数据集中点的个数)往往较少“但这种情况在退化发生时有可能是不对的。

针对经典方法的这几项局限性，有很多改进，在这里提出了一种全局RANSAC(Universal-RANSAC)的结构图，每一种改进方法都可以看做是这种USAC的特例，如下图所示。

2.1 预滤波(Stage 0)

输入数据集

，

含有 N个点，在这一步中，SCRNMSAC[3]，用一个一致性滤波器对初始的数据集进行滤波减少数量，然后将数据根据梯度排序。

2.2 最小子集采样(Stage 1)

对

进行采样时，经典算法采用完全随机的方式，这种方式的前提是我们对数据的情况完全不知道，在实际应用中，很多情况对数据的先验知识是了解的，这对减少采样次数，尤其是类内点比例较低的数据集，有很大帮助，以下是几种在最小集采样当中对经典算法进行改进的方法。

Stage 1.a 采样

2.2.1 NAPSAC[4]

N-Adjacent points sample consensus(NAPSAC)算法认为：”数据集中，一个类内点与数据集中其他类内点的距离比类外点要近。”在一个n维空间中，假定：将数据集的n维空间看做一个超球面，随着半径的减少，类外点减少的速度比类内点要快(类外点距离球心更远)。这种算法可以描述为：

a.

中随机选取一个点 x，设定一个半径 r，以 x为中心 r为半径建立超球面；

b.  超球面内包裹的点少于最小数据集的个数？返回 a，否则c

c.   均匀的从球体内取点，直至满足最小集中的个数。

这种方法对高维、类内点比例低的数据集效果明显，但是容易产生退化，且对于距离都很近的数据集效果差。

2.2.2 PROSAC[5]

The progressive sample consensus(PROSAC)将点初始集匹配的结果作为排序的依据，使得在采样时根据匹配结果由高到低的得分进行排序，这样最有可能得到最佳参数的采样会较早出现，提高了速度。

2.2.3 GroupSAC[6]

与NAPSAC类似，GroupSAC认为类内点更加的“相似”，根据某种相似性将数据集中的点分组。以图像匹配为例，分组可以基于光流聚类(optical flow-based clustering)、图像分割等，然后按照PROSAC思想，采样可以从最大的聚类开始，因为这里应该有更高的类内点比例。但是这种方法首先要保证有一种先验知识可以用于分类，还有就是要保证分类算法的有效性和实时性。

Stage 1.b 采样验证

经典算法在采样完成后开始进行参数计算，而有的算法在采样完成后加了一步验证采样结果适不适合进行参数计算的步骤。比如参数是计算单映性矩阵(4个点)，可以根据chirality constraints 来首先验证采样是否合法。这种验证计算量小，比多余的一次参数计算划算。

2.3 根据最小集产生模型(参数计算)(Stage 2)

Stage 2.a 模型计算

在这一步骤根据上一步选取的最小集计算参数，获得模型。

Stage 2.b 模型验证

还是利用先验知识，比如点集与圆形匹配，验证时候没必要将数据集中所有的点进行验证，而只是在得到模型(圆)的一个半径范围左右验证即可。

2.4 验证参数(Stage 3)

传统的方法在得到最小集产生的参数后计算全部集合中满足参数点的个数(目标函数)，在此，加两步验证，分为两点：第一，验证当前的模型是否可能获得最大的目标函数。第二，当前模型是非退化的。

Stage 3.a 可能性验证

2.4.1 T(d,d)测试[5]

选取远小于数据集综述的 d个点作为测试，只有当这 d个点全都为类内点时，再对剩余的点进行测试，否则抛弃当前的模型。具体选取办法见论文[5].

2.4.2 Bail-Out测试[7]

选取集合中的若干点进行测试，若类内点的比例显著低于当前最佳模型类内点的比例，抛弃此模型。

2.4.3 SPRT测试[8,9]

挨个点测试，

表示随机选取一个点符合当前模型的概率(good),

为“bad”的概率。根据以下公式，当阈值λ超过某阈值的时候抛弃当前模型。

2.4.4 Preemptive测试[10]

ARRSAC算法[11]，首先产生多个模型，而不是产生一个后即对其评价，然后根据选取的一部分子集对所产生的模型按照目标函数得分排序，选取前若干个，做若干轮类似排序，选取最佳模型。

Stage 3.b 退化验证

数据退化的意思是无法提供足够的限制条件产生唯一解。传统RANSAC即没有这种安全的保障。

2.5 模型细化(Stage 4)

含有噪声的数据集有两个重要特点：1，即使子集中全都是类内点，产生的模型也并不一定适用于数据集中所有的类内点，这个现象增加了迭代的次数；2，最终收敛的RANSAC结果可能受到噪声未完全清理的影响，并不是全局最优的结果。

第一个影响往往被忽略，因为虽然增加了迭代次数，但是仍然返回的是一个准确的模型。而第二种影响就要增加一种模型细化的后处理。

2.5.1 局部最优化[12]

Lo-RANSAC，局部最优RANSAC。在迭代过程中，出现当前最优解，进行Lo-RANSAC。一种方法是从返回结果的类内点中再进行采样计算模型，设置一个固定的迭代次数(10-20次)然后选取最优的局部结果作为改进的结果，另一种方法是设置一个优化参数K(2~3)，选取结果中判断阈值(t)小于等于Kt的结果作为优化结果，K减小，直至减小至 t终止。

2.5.1 错误传播法[13]

思想与Lo-RANSAC一致，但是更为直接，因为初始的RANSAC结果产生自含有噪声的数据集，因此这个错误“传播”到了最终的模型，协方差可以看做是估计两个数据集关系是一种不确定的信息(而如上所述，判断阈值的计算是固定的)。具体方法参见文献[13]。

2.6 最终方案--USAC-1.0

最终选取的结果如下图所示：

stage1： 最小集采样方法采用2.2.2节中的PROSAC。

stage3： 模型(参数)验证采用2.4.3的SPRT测试。

stage4： 产生最终模型，采用2.5.1介绍的Lo-RANSAC。

论文翻译自：文献[0]。

----------------------------参考文献---------------------------

[0]  Raguram R, Chum O, Pollefeys M, et al. USAC: A Universal Framework for Random Sample Consensus[J]. Pattern Analysis & Machine Intelligence IEEE Transactions on, 2013, 35(8):2022-2038.

[1] M.A. Fischler and R.C. Bolles, “Random Sample Consensus: A Paradigm for Model Fitting  with Applications to Image Analysis and Automated Cartography,” Comm. ACM, vol. 24, no. 6, pp. 381- 395,1981.

[2] R.I. Hartley and A. Zisserman, Multiple View Geometry in Computer Vision. Cambridge Univ. Press, 2000

[3] T. Sattler, B. Leibe, and L. Kobbelt, “SCRAMSAC: Improving RANSAC’s Efficiency with a Spatial  Consistency Filter,” Proc. 12th IEEE Int’l Conf. Computer Vision, 2009.

[4] D.R. Myatt, P.H.S. Torr, S.J. Nasuto, J.M. Bishop, and R. Craddock,“NAPSAC: High Noise, High  Dimensional Robust Estimation,”Proc. British Machine Vision Conf., pp. 458-467, 2002.

[5] O. Chum and J. Matas, “Matching with PROSAC—Progressive Sample Consensus,” Proc. IEEE Conf. Computer Vision and Pattern Recognition, 2005.

[6] K. Ni, H. Jin, and F. Dellaert, “GroupSAC: Efficient Consensus in the Presence of Groupings,” Proc. 12th IEEE Int’l Conf. Computer Vision, Oct. 2009.

[7] D. Capel, “An Effective Bail-Out Test for RANSAC Consensus Scoring,” Proc. British Machine Vision Conf., 2005.

[8] O. Chum and J. Matas, “Optimal Randomized RANSAC,” IEEE Trans. Pattern Analysis and Machine  Intelligence, vol. 30, no. 8,pp. 1472-1482, Aug. 2008.

[9] J. Matas and O. Chum, “Randomized RANSAC with Sequential Probability Ratio Test,” Proc. 10th IEEE Int’l Conf. Computer Vision,vol. 2, pp. 1727-1732, Oct. 2005.

[10] D. Niste´r, “Preemptive RANSAC for Live Structure and Motion Estimation,” Proc. Ninth IEEE Int’l Conf. Computer Vision, 2003.

[11] R. Raguram, J.-M. Frahm, and M. Pollefeys, “A Comparative Analysis of RANSAC Techniques Leading to Adaptive Real-Time Random Sample Consensus,” Proc. European Conf. Computer Vision, pp. 500- 513. 2008,

[12] O. Chum, J. Matas, and J. Kittler, “Locally Optimized RANSAC,”Proc. DAGM-Symp. Pattern Recognition, pp. 236-243, 2003.

[13] R. Raguram, J.-M Frahm, and M. Pollefeys, “Exploiting Uncertainty in Random Sample Consensus,” Proc. 12th IEEE Int’l Conf. Computer Vision, Oct. 2009.

注：转自 http://blog.csdn.net/tianwaifeimao/article/details/48543361