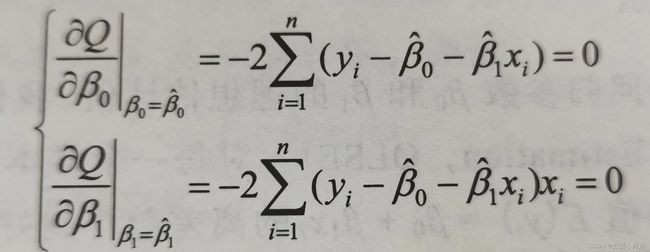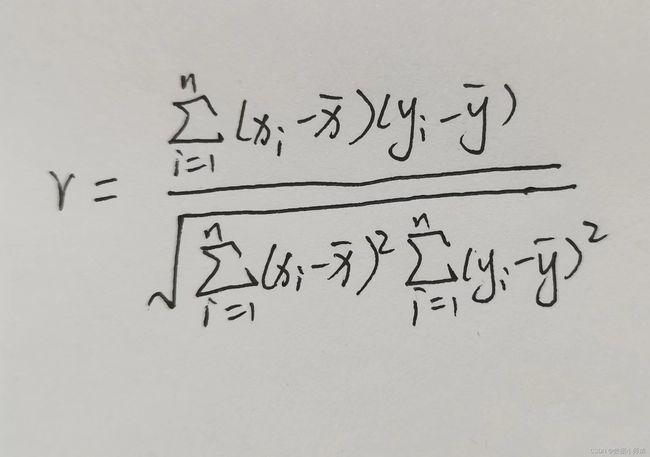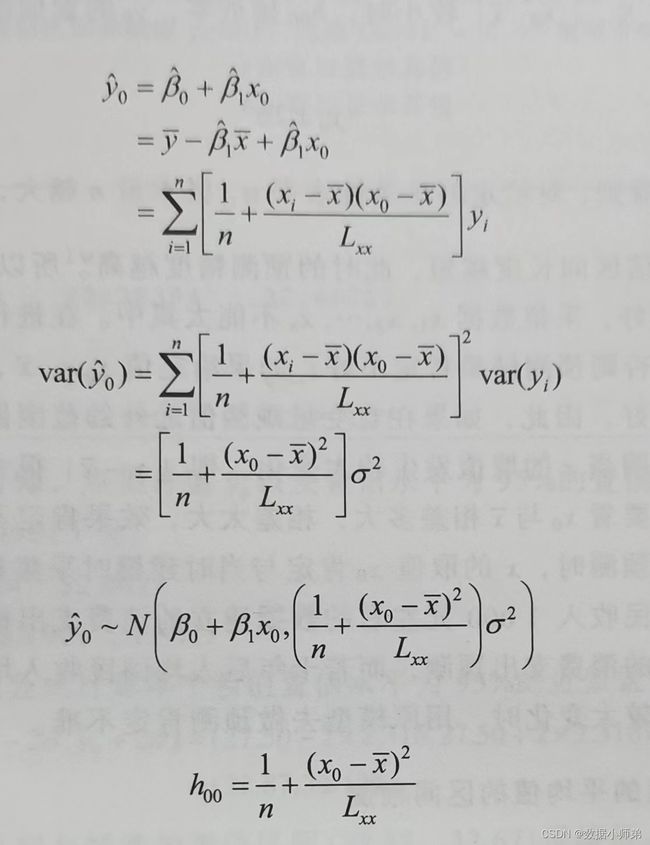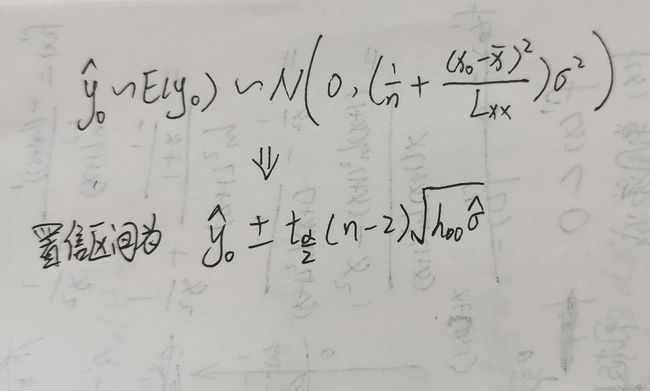一元线性回归模型（保姆级）
提示：本文是基于最小二乘法对数据进行拟合。
目录
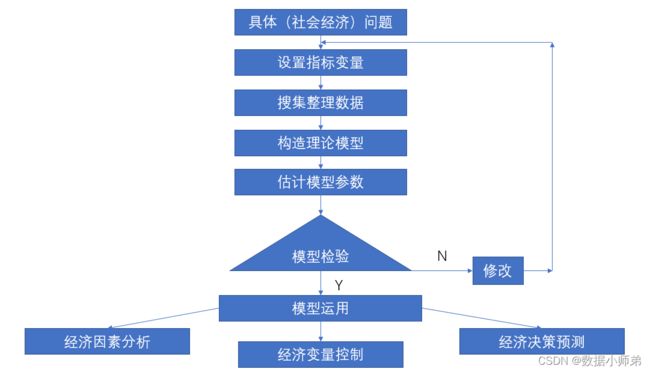
一、模型建立的流程
二、模型原理
1.模型
2、参数编辑 和编辑的估计
三、回归方程的显著性检验
1、t检验
2、F检验
3、相关系数的显著检验
四、残差分析
1、绘画残差图分析
2、改进残差
五、回归系数的区间估计
六、预测和控制
1、单值预测
2、区间预测
（1）、因变量新值的区间估计
（2）、因变量新值平均值的区间预测
七、代码实现
2.读入数据
3、计算相关系数
4、模型拟合
5、画图观察预测的效果
6、方差分析和相关系数检验
7、残差计算
8、改进残差
9、置信区间
10、新值的区间预测
全部代码
总结
一、模型建立的流程
二、模型原理
1.模型
我们建立一元回归模型的形式如下：
y为被解释变量（因变量），x为解释变量（自变量）；
和 
是未知参数，称 为回归常数， 为回归系数，
表示其他随机因素的影响（不可观测的随机误差）。我们一般假设满足
一般我们是不考虑这个随机误差的影响的即建立如下的一元回归模型：
这是我们平常建立的一元回归模型。
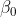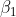2、参数 和的估计
使用最小二乘法对参数进行估计。最小二乘法就是考虑观测值 
与其回归值 
（由于x是已知的数据，即是常数，求期望为原值）的离差越小，最小二乘法就是寻找参数两个参数的估计是 
和 
，使离平方和达到极小，即是参数的估计值。
于是变得到回归拟合值：
残差表达式为
由于残差有正有负，不方便考虑残差的大小，我们就对残差取平方和
于是为了使残差平方和最小，转化成二元变量求极值问题分别对参数求偏导得到
（公式太麻烦了，直接放截图了，嗷嗷~）
接着是化简方程如下
三、回归方程的显著性检验
1、t检验
t检验用于检验回归系数的显著性。原假设是 
，备择假设为 
，如果检验显著，则回归方程结果显著。
给定显著性水平
，双侧检验的临界值为
,当
时，拒绝原假设
所以因变量y对自变量x的一元线性回归成立；当
时，不拒绝原假设 ，所以因变量y对自变量x的一元线性回归不成立。
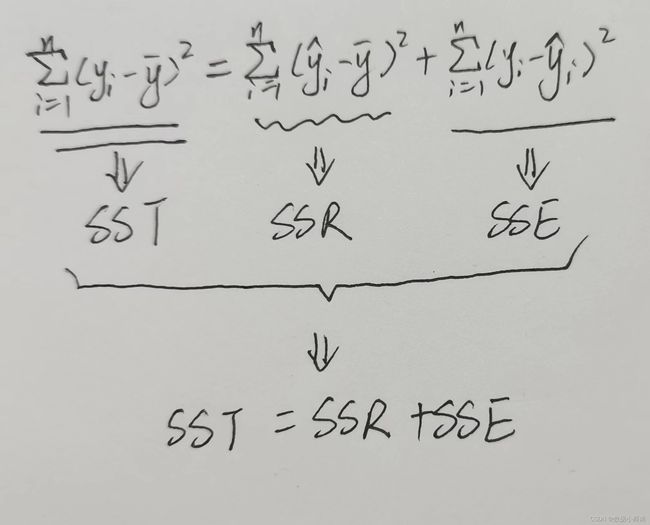
2、F检验
F检验是根据平方和分解式直接对回归效果检验回归方程的显著性。
F检验统计量为：
3、相关系数的显著检验
使用变量x与y之间的相关系数来检验回归方程的显著性：
r的值趋向于1，证明回归方程拟合显著。
四、残差分析
1、绘画残差图分析
这里就没画例子参考的残差图了（bushi）。原理就是分别求出每个点的残差，然后将残差点的位置画在图上。
2、改进残差
一般在残差分析中，认为超过
或者
的残差为异常值。
用这两种方法对残差的异常值进行判断。
五、回归系数的区间估计
首先是对
的区间估计， 同理即可求出。
六、预测和控制
1、单值预测
2、区间预测
（1）、因变量新值的区间估计
求出预测值的均值和方差。
接着就是得到预测值的分布
当样本数量N较大时，置信区间可以为
（2）、因变量新值平均值的区间预测
到这里，一元回归模型的理论就差不多就这些了。接下来就是使用代码实现整个过程了，这里我使用了Python实现。
七、代码实现
1、导入库
导入了numpy进行矩阵运算，statmodels是进行模型拟合的库，matplotlib是画图库，pandas是读取文件和矩阵的相关计算，patsy也是模型拟合的库，scipy是pearson系数的计算库。
代码如下（示例）：
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
import pandas as pd
from patsy import dmatrices
from statsmodels.stats.api import anova_lm
import scipy
2.读入数据
代码如下（示例）：
df = pd.read_csv('data2.1.csv')
3、计算相关系数
代码如下（示例）：
#计算相关系数
cor_matrix = df.corr(method='pearson') # 使用皮尔逊系数计算列与列的相关性4、模型拟合
这里有两种方法，只要学会用其中一种就可以了，当然，两种都学会也Ok。
代码如下（示例）：
#==========第一种建模方式======================================
y,X = dmatrices('y~x', data=df, return_type = 'dataframe')
#print(X)
mod = sm.OLS(y,X)
result = mod.fit()
#==========第二种建模方式（类R语言方式）======================================
result = smf.ols('y~x',data=df).fit()
print(result.summary())通过summary可以得到一元回归的参数情况和显著性情况。
5、画图观察预测的效果
代码如下（示例）：
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(df['x'], df['y'], 'o', label='data')
ax.plot(df['x'], y_fitted, 'r-',label='OLS')
ax.legend(loc='best')
plt.show()6、方差分析和相关系数检验
代码如下（示例）：
#方差分析
table = anova_lm(result, typ=2)
# print(table)
# print(result.scale)
#pearson相关系数检验
cortest = scipy.stats.pearsonr(df['x'],df['y'])
print(cortest)7、残差计算
代码如下（示例）：
#计算残差
eres = result.resid
# print(eres)
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(eres, 'o', label='resid')
# plt.show()8、改进残差
代码如下（示例）：
#标准化残差
stand_eres = eres/np.sqrt(result.scale)#eres.std()
print(stand_eres)
#学生化残差
infl = result.get_influence()
# studentied_eres = infl.summary_table()
studentied_eres = infl.resid_studentized_internal
print(studentied_eres)9、置信区间
代码如下（示例）：
##置信区间
confinterval = result.conf_int(alpha=0.05, cols=None)
print(confinterval)10、新值的区间预测
代码如下（示例）：
#=========预测新值======================================================
#单值
predictvalues = result.predict(pd.DataFrame({'x': [3.5]}))
print(predictvalues)
#区间
predictions = result.get_prediction(pd.DataFrame({'x': [3.5]}))
print(predictions.summary_frame(alpha=0.05))全部代码
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
import pandas as pd
from patsy import dmatrices
from statsmodels.stats.api import anova_lm
import scipy
df = pd.read_csv('data2.1.csv')
# 计算相关系数
cor_matrix = df.corr(method='pearson') # 使用皮尔逊系数计算列与列的相关性
result = smf.ols('y~x', data=df).fit()
#查看参数
print(result.summary())
# 方差分析
table = anova_lm(result, typ=2)
# pearson相关系数检验
cortest = scipy.stats.pearsonr(df['x'], df['y'])
print(cortest)
# 计算残差
eres = result.resid
# 标准化残差
stand_eres = eres / np.sqrt(result.scale) # eres.std()
print(stand_eres)
# 学生化残差
infl = result.get_influence()
studentied_eres = infl.resid_studentized_internal
print(studentied_eres)
##置信区间
confinterval = result.conf_int(alpha=0.05, cols=None)
print(confinterval)
# 单值
predictvalues = result.predict(pd.DataFrame({'x': [3.5]}))
print(predictvalues)
# 区间
predictions = result.get_prediction(pd.DataFrame({'x': [3.5]}))
print(predictions.summary_frame(alpha=0.05))
总结
具体的实现过程代码就已经结束了，有什么不懂的可以评论区交流啦。
看完不要忘了点个赞和关注一下,爱心bui~bui~。