前端秋招笔试高频题JavaScript版解析（一）

---

一、接雨水

问题描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

思路解析

使用动态规划规划的思想解决问题，创建两个长度为n的数组leftMax和rightMax，leftMax[i]表示下标i及其左边的位置中，height的最大高度，rightMax[i]表示下标i及其右边的位置中，height的最大高度。
可以通过正向遍历数组height得到数组中的leftMax的每个值，反向遍历height得到数组rightMax的每个元素值，即可得到下标i处能接的雨水量等于min(leftMax[i], rightMax[i]) - height[i]。

代码实现

var trap = function(height) {
    let res = 0;
    const leftMax = new Array(height.length).fill(height[0]);
    const rightMax = new Array(height.length).fill(height[height.length - 1]);
    for (let i = 1; i < leftMax.length; i++) {
        leftMax[i] = Math.max(height[i], leftMax[i - 1])
    }
    for (let j = rightMax.length - 2; j > -1; j--) {
        rightMax[j] = Math.max(height[j], rightMax[j + 1]);
    }
    for (let i = 0; i < height.length - 1; i++) {
        res += Math.min(leftMax[i], rightMax[i]) - height[i];
    }
    return res;
};

二、字符串压缩

问题描述

字符串压缩。利用字符重复出现的次数，编写一种方法，实现基本的字符串压缩功能。若“压缩”后的字符串没有变短，则返回原先的字符串。你可以假设字符串中只包含大小写英文字母（a至z）

思路解析

采取模拟压缩的思路，从左往右遍历字符串，用res记录压缩的字符串，用num记录重复字符出现次数，迭代中不断更新res并将num重新置0，最后判断长度进行输出。

代码实现

var compressString = function(S) {
    let res = '';
    let num = 1;
    for (let i = 0; i < S.length; i++) {
        while (S[i] === S[i + 1]) {
            num++;
            i++;
        }
        res = res + S[i] + num;
        num = 1;
    }
    return res.length < S.length ? res : S
};

三、网络延迟时间

问题描述

有 n 个网络节点，标记为1到 n。
给定列表times，表示信号经过有向边的传递时间，times[i] = (u_i, v_i, w_i)，其中 u_i 是源节点，v_i 是目标节点， w_i是一个信号从源节点传递到目标节点的时间。
求从某个节点 K 发出一个信号。使所有节点都收到信号所需时间，如果不能使所有节点收到信号，返回-1。

思路分析

采用单源最短路径算法Dijkstra，将所有节点分成两类：已确定从起点到当前点的最短路长度的节点「未确定节点」，以及未确定从起点到当前点的最短路长度的节点「已确定节点」，通过枚举不断将未确定结点更新为已确定结点。求出结点k到其余所有点的最短路，其中的最大值即为答案，若存在无法到达的点则返回-1。

代码实现

var networkDelayTime = function(times, n, k) {
    const INF = Number.MAX_SAFE_INTEGER;
    const g = new Array(n).fill(INF).map(() => new Array(n).fill(INF));
    for (const t of times) {
        const x = t[0] - 1, y = t[1] - 1;
        g[x][y] = t[2];
    }
    const used = new Array(n).fill(false);
    const dist = new Array(n).fill(INF);
    dist[k - 1] = 0;
    for (let i = 0; i < n; i++) {
        let x = -1;
        for (let y = 0; y < n; y++) {
            if (!used[y] && (x === -1 || dist[y] < dist[x])) {
                x = y;
            }
        }
        used[x] = true;
        for (let y = 0; y < n; y++) {
            dist[y] = Math.min(dist[y], dist[x] + g[x][y])
        }
    }
    let res = Math.max(...dist);
    return res === INF ? -1 : res
};

四、翻转字符串中的单词

问题描述

给你一个字符串s，其中单词是由非空格字符组成的字符串，由至少一个空格分隔开，返回单词顺序颠倒且单词之间用单个空格连接的结果字符串。

思路分析

使用双指针的方法，从后向前遍历字符。右端的指针遇到空格跳过，直到单词的末尾，然后将左端的指针指向右端。
之后左指针继续向前，直到遇到空格或小于0才停下，此时左右指针之间就是单词，把单词添加到结果字符串中，然后把右指针指向左指针，开始下一轮遍历，
下一轮遍历开始后，如果还有新单词，就给上一个单词后面添加一个空格
代码。

代码实现

var reverseWords = function(s) {
    let right = s.length - 1, left = right;
    let res = '';
    while (left >= 0) {
        while (s[right] === ' ') {
            right--;
        }
        left = right;
        if (left >= 0 && res) {
            res += ' ';
        }
        while (s[left] && s[left] !== ' ') {
            left--;
        }
        for (let i = left + 1, j = right; i <= j; i++) {
            res += s[i]
        }
        right = left;
    }
    return res
};

五、最近时刻

问题描述

给定格式为HH:MM的时刻time，利用当前出现过的数字构造下一个距离当前时间最近的时刻。每个出现数字都可以被无限次使用。

思路分析

模拟时钟前进一分钟。每次向前移动时，如果当前时间能够被构造，则返回当前时间。
表示时间的方法是在0<=t<24*60范围内以整数 t 表示。然后小时数是Math.floor(t/60)，分钟数是t%60。

代码实现

const nextClosestTime = function(time) {
  const [hour, minute] = time.split(':')
  const nums = new Set()
  for (const num of time) {
    if (num === ':') continue
    nums.add(num)
  }

  const timestmap = hour * 60 + +minute
  const max = 23 * 60 + 59
  for (let t = timestmap + 1; t <= max; t++) {
    const ans = convert(t, nums)
    if (ans) return ans
  }
  for (let t = 0; t < timestmap; t++) {
    const ans = convert(t, nums)
    if (ans) return ans
  }
  return time

  function convert(time, nums) {
    const m = time % 60
    const h = Math.trunc(time / 60)
    if ((h < 10 || m < 10) && !nums.has('0')) return false
    for (const c of (m + '' + h)) {
      if (!nums.has(c)) return false
    }
    return (h < 10 ? '0' + h : h) + ':' + (m < 10 ? '0' + m : m)
  }
};

六、单词搜索

问题描述

给定一个二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。
单词必须按照字母顺序，通过相邻的单元格内的字母构成，同一个单元格内的字母不允许被重复使用。

思路分析

采取深度优先算法DFS+回溯的思路，并用了一个二维数组mark对使用过的元素做标记。
首先遍历 board 的所有元素，先找到和 word 第一个字母相同的元素，然后进入递归流程。在递归中判断元素上下左右是否能匹配 word 的下一个字母，满足则继续递归。

代码实现

const exist = (broad, word) => {
    const m = broad.length;
    const n = broad[0].length;
    const used = new Array(m).fill(false).map(() => new Array(n).fill(false));
    const canFind = (row, col, i) => {
        if (i === word.length) {
            return true;
        }
        if (row < 0 || row >= m || col < 0 || col >=n) {
            return false
        }
        if (used[row][col] === true || broad[row][col] !== word[i]) {
            return false;
        }
        used[row][col] = true;
        const canFindRest = canFind(row + 1, col, i + 1) || canFind(row - 1, col, i + 1) ||
            canFind(row, col + 1, i + 1) || canFind(row, col - 1, i + 1); 

        if (canFindRest) {
            return true;    
        }
        used[row][col] = false;
        return false;
    }
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (broad[i][j] === word[0] && canFind(i, j, 0)) {
                return true
            }
        }
    }
    return false;
}

七、最大数

问题描述

给定一组非负整数nums，重新排列每个数的顺序（每个数不可拆分）使之组成一个最大的整数（字符串形式）。

思路分析

对数组进行排序后输出字符串即可。

代码实现

var largestNumber = function(nums) {
    nums.sort((a, b) => {
        return `${b}${a}` - `${a}${b}`
    })
    let i = 0;
    while (nums[i] == 0 && i !== nums.length - 1) {
        i++;
    }
    return nums.slice(i).join('')
}

八、矩形面积

问题描述

给你 二维 平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形，请你计算并返回两个矩形覆盖的总面积。
每个矩形由其左下顶点和 右上顶点坐标表示：
第一个矩形由其左下顶点(a_x1, a_y1)和右上顶点(a_x2, a_y2)定义。
第二个矩形由其左下顶点(b_x1, b_y1)和右上顶点(b_x2, b_y2)定义。

思路分析

首先计算两个矩形总面积，之后判断是否重叠，如发生重叠则减去重叠区域面积。

代码实现

var computeArea = function(ax1, ay1, ax2, ay2, bx1, by1, bx2, by2) {
    const area = (ax2 - ax1) * (ay2 - ay1) + (bx2 - bx1) * (by2 - by1);
    const cx1 = Math.max(ax1, bx1);
    const cy1 = Math.max(ay1, by1);
    const cx2 = Math.min(ax2, bx2);
    const cy2 = Math.min(ay2, by2);
    if (cx2 > cx1 && cy2 > cy1) {
        return area - (cx2 - cx1) * (cy2 - cy1)
    }
    return area
};

九、根据字符串出现频率排序

问题描述

给定一个字符串s，根据字符出现的频率对其进行降序排序 。一个字符出现的频率 是它出现在字符串中的次数。

思路分析

首先借助哈希表Map储存字符串出现次数，之后根据出现出现字符对字符进行降序操作，再进行输出。

代码实现

var frequencySort = function(s) {
    const newMap = new Map();
    for (let char of s) {
        newMap.set(char, (newMap.get(char) || 0) + 1)
    }
    const list = [...newMap.keys()];
    list.sort((a, b) => newMap.get(b) - newMap.get(a));
    let res = '';
    for (let i = 0; i < list.length; i++) {
        const char = list[i];
        const frequency = newMap.get(char);
        for (let j = 0; j < frequency; j++) {
            res += char
        }
    }
    return res
};

十、岛屿数量

问题描述

给定由 1（陆地）和 0（水）组成的的二维网格，计算网格中岛屿的数量。
岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

思路分析

我们可以将二维网格看成一个无向图，竖直或水平相邻的1之间有边相连。
为了求出岛屿的数量，我们可以扫描整个二维网格。如果一个位置为 11，则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中，每个搜索到的1都会被重新标记为0。
最终岛屿的数量就是我们进行深度优先搜索的次数。

代码实现

var numIslands = function(grid) {
    let res = 0;
    const m = grid.length;
    const n = grid[0].length;
    const getLand = (row, col, grid) => {
        if (row < 0 || col <0 || row >= m || col >= n) {
            return;
        }
        if (grid[row][col] == '0') {
            return;
        } else {
            grid[row][col] = '0'
        }
        getLand(row - 1, col, grid);
        getLand(row + 1, col, grid);
        getLand(row, col - 1, grid);
        getLand(row, col + 1, grid);
    }
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (grid[i][j] == '1') {
                res++;
                getLand(i, j, grid);
            }
        }
    }
    return res;
};

十一、三数之和

问题描述

给你一个整数数组 nums ，判断是否存在三元组[nums[i], nums[j], nums[k]]满足i != j、i != k且 j != k，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
返回所有和为0且不重复的三元组。

思路分析

采取排序+双指针的思路，不断迭代寻求复合解。

代码实现

var threeSum = function(nums) {
  const result = [];
  if (nums.length < 3) {
    return result;
  }
  nums = nums.sort((a, b) => a - b);
  for (let i = 0; i < nums.length; i++) {
    // 剪枝
    if (nums[i] > 0) {
      break;
    }

    if (i > 0 && nums[i] === nums[i - 1]) {
      continue;
    }
    let left = i + 1, right = nums.length - 1;
    while (left < right) {
      const sum = nums[left] + nums[right] + nums[i];
      if (sum > 0) {
        right--;
      } else if (sum < 0) {
        left++;
      } else {
        // 符合要求
        result.push([nums[i], nums[left], nums[right]]);
        left++;
        right--;
        // 避免重复
        while (left < right && nums[left] === nums[left - 1]) left++;
        while (left < right && nums[right] === nums[right + 1]) right--;
      }
    }
  }
  return result;
};

十二、爬楼梯

问题描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶，每次你可以爬1或 2 个台阶，求可选方案数。

思路分析

利用转移方程f(x)=f(x−1)+f(x−2)，迭代进行动态规划。

代码实现

var climbStairs = function(n) {
    const res = [];
    res[0] = 1;
    res[1] = 2;
    for (let i = 2; i < n; i++) {
        res[i] = res[i - 1] + res[i - 2];
    }
    return res[n - 1]
};

十三、腐烂的橘子

问题描述

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：0代表空单元格，1代表新鲜橘子，2代表腐烂的橘子。
每分钟，腐烂的橘子周围4个方向上相邻的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

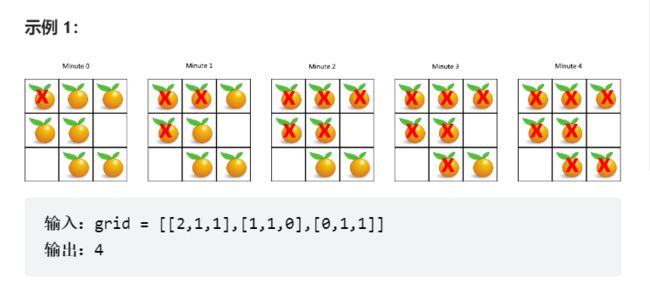
思路分析

采用广度优先算法BFS思想，层序遍历grid，每次将腐烂的橘子置为1并记录层序遍历次数，新鲜橘子树为0或遍历结束时进行判断，输出输出时间。

代码实现

var orangesRotting = function(grid) {
    const m = grid.length, n = grid[0].length;
    let fresh = 0;
    let badArr = []
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (grid[i][j] == 1) {
                fresh++;
            }
            if (grid[i][j] == 2) {
                badArr.push([i, j])
            }
        }
    }
    let time = 0;
    const dire = [[0, -1], [-1, 0], [0, 1], [1, 0]];
    while (badArr.length != 0 && fresh) {
        const newArr = [];
         while (badArr.length != 0) {
            let current = badArr.pop();
            for (let i = 0; i < dire.length; i++) {
                let row = current[0] + dire[i][0];
                let col = current[1] + dire[i][1];
                // 边界
                if (row >= 0 && col >= 0 && row < m && col < n) {
                    //变腐烂且入队列,新鲜减1
                    if (grid[row][col] == 1) {
                        grid[row][col] = 2;
                        newArr.push([row, col]);
                        fresh--;
                    }
                }
            }
        }
        time++;
        badArr = newArr;
    }
    return fresh == 0 ? time : -1
};

十四、最小绝对差

问题描述

给定整数数组 arr，其中每个元素都不相同。找到所有具有最小绝对差的元素对，并且按升序的顺序返回。

思路分析

采用排序+一次遍历方式即可。

代码实现

var minimumAbsDifference = function(arr) {
    let res = [];
    arr.sort((a, b) => a - b);
    let min = Number.MAX_VALUE;
    for (let i = 1; i < arr.length; i++) {
        let temp = arr[i] - arr[i - 1];
        if (temp < min) {
            res = [];
            min = temp;
        }
        if (temp == min) {
            res.push([arr[i - 1], arr[i]])
        }
    }
    return res
};

十五、外观数列

问题描述

给定一个正整数n，输出外观数列的第 n 项。
「外观数列」是一个整数序列，从数字 1 开始，序列中的每一项都是对前一项的描述。

思路分析

通过遍历生成外观序列。

代码实现

var countAndSay = function(n) {
    let char = '1';
    for (let i = 1; i < n; i++) {
        let newChar = '';
        let temp = char[0];
        let start = 0;
        let pos = 0;
        while (pos < char.length) {
            while (pos < char.length && char[pos] === char[start]) {
                pos++;
            }
            newChar = newChar + (pos - start) + char[start];
            start = pos;
        }
        char = newChar
    }
    return char
};