【论文阅读】Coupled Iterative Refinement for 6D Multi-Object Pose Estimation

随缘更新

一篇被CVPR2022接收，有关6D位姿估计的文章

论文链接：Coupled Iterative Refinement for 6D Multi-Object Pose Estimation

论文代码：Github

---

主要内容和贡献

本文提出了一个能够利用几何信息的端到端的可微分结构 (differentiable architecture)，用一种紧密耦合的方式迭代地对pose和correspondence共同进行refine，动态地移除外点 (outliers)，进而提高预测准确率。

本文提出的结构命名为 BD-PnP，即 Bidirectional Depth-Augmented Perspective-N-Point

“We use a novel differentiable layer to perform pose refinement by solving an optimization problem.”

相关工作

传统方法

• 早期的6D位姿估计利用具备不变性的局部特征得到2D图片像素点和3D模型点之间的对应 (correspondence)，然后在对应点集的基础上利用 PnP 估计6D的物体位姿。注意这里所说的点集其实就是一部分匹配点，即2D像素点和3D模型点的匹配，所以一张图片只会选出一小部分能够匹配的点进行位姿估计，即 sparse matches

• 利用2D-3D响应得到位姿的方法主要有 closed form 和 iterative algorithm 两种，一般使用 closed form solution 进行初始化，然后在接下来的过程中使用 iterative refinement。

• 由于外点 (outliers) 的存在，常用RANSAC用于移除外点，增加鲁棒性。

缺陷：传统方法使用的局部特征非常依赖纹理，如果纹理不清晰不明显，则产生的correspondence不足以支撑产生准确率高的位姿。

改进：本文也是在2D图像和3D模型之间产生响应，但是不同于传统方法的sparse matches，本文产生的是dense correspondence field，即对于一张输入图片，利用3D模型渲染多个视图，输入图片和每个视图都产生像素级别的置信权重，进而保证足够数量的匹配点。

基于学习的方法

有两种方法：一、直接回归旋转和平移参数；二、通过检测和回归关键点 (keypoints) 生成2D-3D对应；

我们主要聚焦第二种方法，如何回归出关键点：

• 一种方法是回归关键点的在位姿对应的坐标系下的三维坐标，代表方法有Pixel2Pose、BB8等。通过回归object coordinates，就能产生一个密集的2D-3D correspondence的集合，然后用PnP得到位姿，值得一提的是，BPNP 把 PnP solvers 实现成了一个可微分的网络层，让网络可以实现端到端而不用单独做PnP，本文的思路也和BPNP相似。
• 另一种方法就是回归出三维点的编码，比如我在之前的文章中写到的这种 【论文阅读】ZebraPose: Coarse to Fine Surface Encoding for 6DoF Object Pose Estimation，这里不做过多讨论。

缺陷：correspondence的产生和PnP solvers的运作是两个独立的过程，产生的correspondence在后一个过程中是固定不变的，如果前者结果不好，那么PnP的结果自然就不好。

改进：本文以光流的方式直接回归出2D-3D correspondence，并且在迭代的过程中同时对correspondence和pose进行refine，也就是说correspondence不再是固定的了，而是可以进行refine更新的。

iterative refinement

single-shot setting并不能产生高准确率的位姿，所以iterative refinement广泛用于提高位姿估计的准确性。这里主要提到两种代表性的方法：

• DeepIM & CosyPose，DeepIM是一种迭代的“渲染-比较”方法，在每轮迭代中，用当前预测结果渲染3D模型，然后用渲染图和真实图回归一个pose update，用于更新当前的位姿以更好地进行对齐。CosyPose在DeepIM的思想上使用了更好的网络结构和旋转参数化。
• RAFT-3D，在场景流估计的上下文 (context of scene flow estimation) 中进行iterative refinement，在光流refinement和拟合刚体变换之间迭代。RAFT-3D applies iterative refinement in the context of scene flow estimation, they iterate between optical flow refinement and fitting rigid body transformations.

本文提出的方法和上述两种方法都有相似之处。

和DeepIM一样都包含outer loop，即用当前的预测位姿重新渲染三维模型然后对预测的位姿进行更新，但是更新所用的pose update并不是和DeepIM一样直接回归得到的，而是用本文提出的BD-PnP产生的，前文也提到了，BD-PnP能利用几何约束，这是相较于DeepIM直接回归方法进行了改良的地方。

和RAFT-3D的iterative refinement策略是相同的，但是预测刚体变换的方法是用本文提出的BD-PnP layer，而不是RAFT-3D中使用的Dense-SE3。

模型架构

输入：一张RGB-D图片

输出：一组物体的位姿估计

三个阶段：1和2沿用了CosyPose的方法，本文主要聚焦3

1. object detection
2. pose initialization
3. pose refinement，用subpixel reprojection error（子像素重投影误差）把初始的coarse位姿转变成refined位姿

预备知识

• 对于给定的有纹理的三维模型，可以用PyTorch3D和相机的内参矩阵 $K_i$ 、外参矩阵 $G_i$ 渲染不同视角下的图像和深度图

  $G_i=\left(\begin{array}{ll}R& t\\ 0& 1\end{array}\right)$, $K_i=\left(\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right)$

  $G_i$ 是物体在相机坐标系下的位姿，则对于一张输入图片来说，$G_0$ 是输入图片的位姿，$\{G_1,\cdots ,G_N\}$ 是N张渲染图片的位姿，定义两种方法用来索引二者点之间的映射关系：

  ① ${\mathbf{x}}_{i\to 0}^{\prime }=\Pi \left({\mathbf{G}}_0{\mathbf{G}}_i^{-1}{\Pi }^{-1}\left({\mathbf{x}}_i\right)\right)$ 表示渲染图片到输入图片的点的映射。

  ② ${\mathbf{x}}_{0\to i}^{\prime }=\Pi \left({\mathbf{G}}_i{\mathbf{G}}_0^{-1}{\Pi }^{-1}\left({\mathbf{x}}_0\right)\right)$ 表示从输入图片到渲染图片的点的映射。

  其中 $\Pi$ 和 ${\Pi }^{-1}$ 是 depth-augmented pinhole projection functions （深度增强的针孔投影函数），不仅能转换图片上点的坐标，还能转换帧之间的逆深度（深度的倒数）

  $\Pi (\mathbf{X})=\left[\begin{array}{l}X/Z\\ Y/Z\\ 1/Z\end{array}\right]{\Pi }^{-1}(\mathbf{x})=\left[\begin{array}{l}x/d\\ y/d\\ 1/d\end{array}\right]\mathbf{x}=\left[\begin{array}{l}x\\ y\\ d\end{array}\right]$

  注意，上面的像素坐标要用内参矩阵 $K_i$ 进行规范化。

  我们最终的目标就是要不断优化G0（输入图片的位姿）使得xi-0正确，也就是使渲染图片到输入图片的点的映射是正确的

• 目标检测：为了检测到输入图片中的物体，用bounding box截取出来。

• 初始化：并行处理每个候选物体，得到 $G_0^{(0)}$

• 特征抽取和相关性计算：

  对于给定的初始位姿，在位姿估计的基础上渲染几个视图，然后在仰角、俯角、偏航角上加上或减去22.5度，总共得到7个渲染视图。

  对每个渲染图片，本文的网络结构都得到输入的图片（经过裁剪后）和渲染图片之间的双向dense correspondence。

  渲染图片的位姿是已知的，输入图片的物体位姿是要估计的。

  所有图片都抽取一个 $\frac{H}{4}\times \frac{W}{4}$​ 的特征图，对每一个“image-render”对都建立两个correlation volume，一个是从输入图片到渲染图片的，一个是从渲染图片到输入图片的。correlation volume的计算方式是对所有特征向量对做点积运算得到的，然后像RAFT一样把correlation volume的最后两个维度做池化，产生一个4层的相关性金字塔（correlation pyramids），这个金字塔包含了匹配所用的correlation features。
  

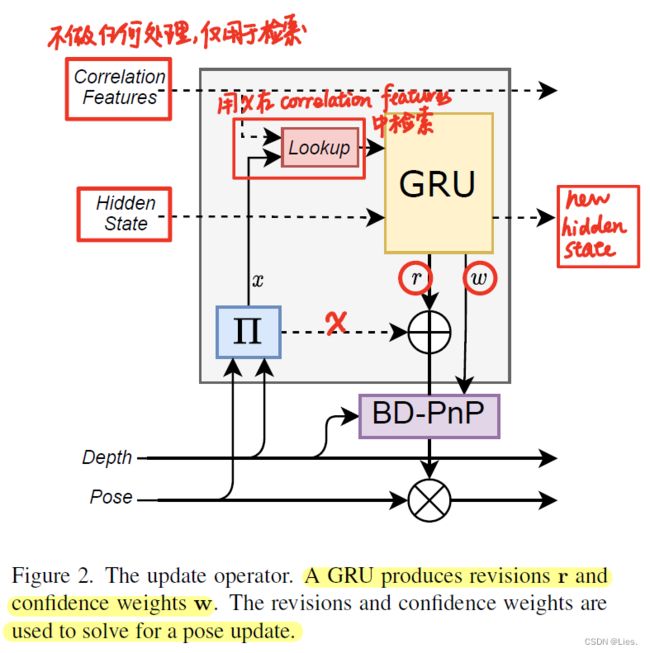
Coupled Iterative Refinement

用下图的结构生成一个姿态估计的更新序列。

左下角部分的输入和 $\Pi$ 主要包含下面两个部分：

• $\mathbf{G}=\{G_0,G_1,\cdots ,G_7\}$ 是所有位姿的集合，其中 $G_1$ 到 $G_7$ 是渲染图片的位姿，是固定的，$G_0$ 是输入图片的位姿，是可变的。

• 计算 $G_0$ 到 $G_i(i=1,2,\cdots ,7)$ 的dense correspondence field $x_{0\to i}$
  计算 $G_i$ 到 $G_0$ 的dense correspondence field $x_{i\to 0}$

  这部分体现的是模型的bidirection

  $x_{i\to 0}$的维度是$H\times W\times 3$ ，表示渲染图片 $i$ 中的每个像素在输入图片的2D坐标，还有逆深度信息。

  同时得到corresponding correlation pyramid

Correlation Lookup

产生 ${\mathbf{s}}_{i\to 0}$ 和 ${\mathbf{s}}_{0\to i}$

• 用 $x_{i\to 0}$ 从相关性金字塔中索引（RAFT的方法），correlation lookup对每个点都在半径为 $r$ 的范围内对相关金字塔的每一层进行索引，得到 $L$ 个correlation feature，最终得到一个correlation feature的映射关系 ${\mathbf{s}}_{i\to 0}\in {\mathbb{R}}^{H\times W\times L}$
• 同理，对 $x_{0\to i}$ 得到 ${\mathbf{s}}_{0\to i}\in {\mathbb{R}}^{H\times W\times L}$

GRU Update

产生 $h_{i\to 0},h_{0\to i}$、 ${\mathbf{r}}_{i\to 0},w_{i\to 0}$ 和 ${\mathbf{r}}_{0\to i},w_{0\to i}$

结构图的GRU是个 $3\times 3$ 的convolution GRU，对每个"image-render"对来说，GRU的输入有四个：（以 $i\to 0$ 的方向为例，$0\to i$ 的同理）

• correlation feature ${\mathbf{s}}_{i\to 0}$
• hidden state $h_{i\to 0}$
• additional context（在论文的appendix中提到，是个不变的feature）
• depth features（在论文的appendix中提到，是变化的）

产生三个输出：

• 新的hidden state $h_{i\to 0}$
• 修正值 (revision) ${\mathbf{r}}_{i\to 0}$ ，维度为 $H\times W\times 3$，3是指在2D坐标和逆深度的修正值
• 置信度（权重）$w_{i\to 0}$ ，维度是 $H\times W$，代表每个位置修正值的权重

论文中解释了深度修正值的必要性，是补偿输入传感器深度可能有噪声和相应点可能被遮挡的问题。

同时论文中也说明了在两个方向的计算过程中，GRU的权重是共享的。

Bidirectional Depth-Augmented PnP (BD-PnP)

这部分是以修正值 r 和置信度 w 来产生一个相机位姿的更新值 $\Delta G_0$ ，分为以下几个步骤：

1. 用修正值更新correspondence fields
   $\mathbf{x}{’}_{i\to 0}={\mathbf{x}}_{i\to 0}+{\mathbf{r}}_{i\to 0}$
   $\mathbf{x}{’}_{0\to i}={\mathbf{x}}_{0\to i}+{\mathbf{r}}_{0\to i}$

2. 定义目标函数

   $\mathbf{E}\left({\mathbf{G}}_0\right)={\sum }_{i=1}^N\Vert {\mathbf{x}}_{i\to 0}^{\prime }-\Pi ({\mathbf{G}}_0{\mathbf{G}}_i^{-1}{\Pi }^{-1}\left({\mathbf{x}}_i\right){\Vert }_{{\Sigma }_{i\to 0}}^2+{\sum }_{i=1}^N\Vert {\mathbf{x}}_{0\to i}^{\prime }-\Pi ({\mathbf{G}}_i{\mathbf{G}}_0^{-1}{\Pi }^{-1}\left({\mathbf{x}}_0\right){\Vert }_{{\Sigma }_{0\to i}}^2$

   最小化这个重投影坐标和修正后的correspondence的距离，距离函数$||\cdot |{|}_{\sum }$是马氏距离（Mahalanobis distance），${\sum }_{i\to 0}$ 是 $w_{i\to 0}$ 的对角线元素。

   马氏距离衡量了一个点到一个分布的距离

   这个目标函数的意义是得到一个相机坐标 $G_0$ ，使重投影的点能够匹配修正后的correspondence ${\mathbf{x}}_{ij}^{\prime }$

3. Gauss-Netwon updates

   每次迭代都会产生一个 $\delta \xi \in SE(3)$ ，然后用当前的位姿叠加这个修正值得到更新一次后的位姿 $G_0^{(t+1)}=\exp (\delta \xi )\cdot G_0^{(t)}$

   在训练时迭代3次，在推理时迭代10次（这里我其实没懂到底是哪个步骤）

第二步最小化目标函数很像PnP，但是PnP只用了单个的2D-3D对应关系，而本文的方法使用了两个（正向和反向），除此以外，本文的方法包含了逆深度的重投影误差，这在PnP中是不具备的。

Inner and Outer Update Loops

• 给定一个渲染图片的集合，跑40轮update，然后用更新后的位姿估计重新渲染新的图片得到一个集合。
• 用得到的新集合重复上一个步骤

第一步就是inner loop，第二步就是outer loop。也就是用更好的位姿估计重新渲染7个视角的图片，然后再更新位姿估计，如此循环。

增加inner loop和outer loop的次数，就能达到用速度换准确度 (trade speed for accuracy) 的目的

RGB图片的处理

实验部分