论文阅读《Multi-View Depth Estimation by Fusing Single-View Depth Probability with Multi-View Geometry》

论文地址：https://arxiv.org/abs/2112.08177
源码地址：https://github.com/baegwangbin/MaGNet

---

概述

出发点：

• MVS构建多视角匹配代价体带来巨大的显存消耗
• 单目深度估计在无（弱）纹理区域、反射表面、运动的物体的情况下的的估计效果比好
    为此，本文提出一种融合了单视图深度概率与多视图几何的新框架(Monocular and Geometric Network : MaGNet)，对于每一帧图像，MaGNet预测单视图的深度概率分布，并将其参数化为像素级别的高斯分布；然后，将参考帧估计的分布用于采样素深度假设值。这种概率采样策略使得网络可以建立较少的深度假设值的同时获得更高的精度；文中还对多视图匹配得分提出深度一致性加权，以确保多视图深度与单视图预测一致。
  文章的创新点如下：
• Probabilistic depth sampling（基于概率分布的深度值采样）：从单目估计中得到概率分布，使用概率分布生成深度假设值；
• Depth consistency weighting for multi-view matching（多视图深度一致性权重）：使用单视图的深度概率分布来生成多视图匹配权重，对多视图匹配结果进行加权；
• Iterative refinement（迭代优化策略）：使用概率分布构建的深度假设体与多视图一致性权重构建得到紧凑的初始匹配代价体，若单视图的深度概率分布有误差，导致无法采样得到深度假设值。针对这种情况提出了基于迭代优化的策略，将更新后的概率分布反馈到概率深度采样模块，不断提升概率分布的准确性；

主要包含以下几个步骤：

1. 预测单帧图像深度概率分布，并将其参数化为高斯分布；
2. 使用预测的分布来对参考图像的每个像素的深度采样得到深度假设值；
3. 使用深度假设值与相机参数将参考帧的特征warp到邻域帧，通过点乘的方式计算匹配代价；
4. 每个相邻视图的匹配分数乘以从该视图估计的单视图深度概率推断出的二元深度一致性权重；
5. 使用匹配代价体经过代价体正则化得到匹配概率体；
6. 步骤2-5可以重复迭代来提高精度；

通过这种方式，最终输出是逐像素深度概率分布图，从中可以推断出期望值和相关的不确定性。

---

模型架构

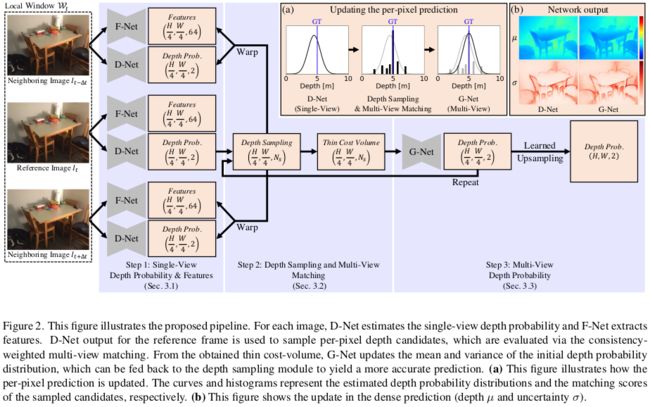
  模型的目标为预测参考帧 $I_t$ 在 t 时刻的深度图，输入为一段时间序列内的图片：${\mathcal{W}}_t=\left\{I_{t-2\Delta t},I_{t-\Delta t},I_t,I_{t+\Delta t},I_{t+2\Delta t}\right\}$ 与相机参数，如图2所示，主要包含以下3个步骤：1. 对每一帧图像进行特征提取与深度概率分布预测；2. 通过概率分布来进行深度假设值采样，并生成多视图一致性权重；3. 使用匹配代价体来估计多视图深度概率体；

Single-View Depth Probability and Features（单视图特征提取与深度概率分布构建）

Single-view depth probability

  对于${\mathcal{W}}_t\in R^{H\times W}$中的每张输入的图像 $I_t$，使用D-Net来预测其深度概率分布图 $\in R^{\frac{H}{4}\times \frac{W}{4}}$，对于 $I_t$ 每一个像素点 $(u,v)$ ，将其概率分布参数化如式1所示：
$$p_{u,v}\left(d\mid I_t\right)=\frac{1}{{\sigma }_{u,v}\left(I_t\right)\sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{d-{\mu }_{u,v}\left(I_t\right)}{{\sigma }_{u,v}\left(I_t\right)}\right)}^2}\text{\hspace{1em}(1)}$$
其中 $\mu 和\sigma$ 是均值与方差，文中使用一个轻量级的编解码结构和EfficientNet B5来作为主干网络，使用线性激活层来计算均值$\mu$ ，使用修正的ELU函数来计算方差 $\sigma$ ：$f(x)=ELU(x)+1$，由此来保证计得到的方差为正，且具有平滑的梯度；当训练其余的模块时需要将D-Net的权值冻结；使用NLL损失来监督模型训练：
$$L_{u,v}\left(d_{u,v}^{\mathrm{g}\mathrm{t}}\mid I_t\right)=\frac{1}{2}\log {\sigma }_{u,v}^2\left(I_t\right)+\frac{{\left(d_{u,v}^{\mathrm{g}\mathrm{t}}-{\mu }_{u,v}\left(I_t\right)\right)}^2}{2{\sigma }_{u,v}^2\left(I_t\right)}\text{\hspace{1em}(2)}$$
上式表示，在物体边界点，当模型难以减小 $(d^{gt}-\mu {)}^2$ 的误差，就会使得标准差 ${\sigma }^2$ 较大来使得第二项变小，第一项会限制方差过大；在非边界区域，此时正确的深度值与估计的 $\mu$ 相近，第二项近似为0，为了使整个损失函数较小，模型会趋向于将第一项变小，也就是${\sigma }^2$ 较小；

Single-view features

  使用F-Net来提取每张图片的特征 $\in R^{\frac{H}{4}\times \frac{W}{4}}$，然后基于对应点特征向量点乘的方式计算匹配代价体，对于像素点 $(u,v)$ 在深度 $\{d_k{\}}_{k=1}^{N_s}$，其匹配代价如式3所示：
$$s_{u,v,k}\left(I_t\right)=\sum _{i\ne t}⟨{\mathbf{f}}_{u,v}\left(I_t\right),{\mathbf{f}}_{u_{ik},v_{ik}}\left(I_i\right)⟩\text{\hspace{1em}(3)}$$

  在depth维度进行softmax得到概率体$p_{u,v,k}=sofrma{x}_k(s_{u,v,k})$，最后基于期望来计算深度图${\hat{d}}_{u,v}={\sum }_k{p}_{u,v,k}\cdot d_k$，F-Net通过均匀采样的深度假设体 $\{d_k\}$ 和最小化$\widehat{d_{u,v}}与d_{u,v}^{gt}$ 之间的 L1来得到预训练权重；

Fusing Single-View Depth Probability with Multi-View Geometry（单视图深度概率分布与多视角几何信息融合）

注:此过程是无可学习的参数（不需要梯度下降）

Probabilistic depth sampling(基于概率分布的深度假设值采样)

   文中定义每个像素的深度假设值搜索范围为 $[{\mu }_{u,v}-\beta {\sigma }_{u,v},{\mu }_{u,v}+\beta {\sigma }_{u,v}]$， $\beta$ 为一个超参数，然后将搜索范围等分为10个区间，这样使得更多的深度假设值能接近 ${\mu }_{u,v}$ ,每个区间的中点为深度假设值，第k个深度假设值 $d_{u,v,k}$ 定义如式4所示：
$$\begin{gathered} d_{u,v,k}={\mu }_{u,v}+b_k{\sigma }_{u,v} \\ where\begin{array}{rlr}{b}_k=\frac{1}{2}[& {\Phi }^{-1}\left(\frac{k-1}{N_s}{P}^{\ast }+\frac{1-P^{\ast }}{2}\right)& +{\Phi }^{-1}\left(\frac{k}{N_s}{P}^{\ast }+\frac{1-P^{\ast }}{2}\right)]\end{array}\text{\hspace{1em}(4)} \end{gathered}$$
其中，${\Phi }^{-1}(.)$ 是概率函数，而 $P^{\star }=erf(\beta /\sqrt{2})$ 表示区间 $[{\mu }_{u,v}-\beta {\sigma }_{u,v},{\mu }_{u,v}+\beta {\sigma }_{u,v}]$ 的概率质量；
注：$\{b_k\}$ 只与 $N_s$ 和 $\beta$ 有关，不需要逐像素计算；

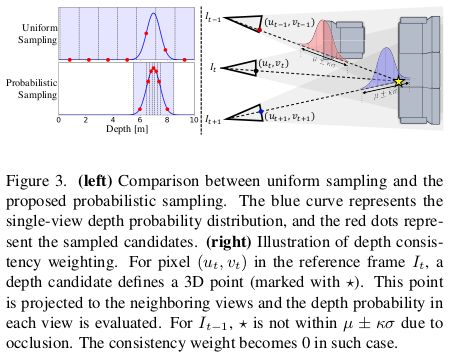
图3左侧对比了均匀采样与本文提出的采样方式，对于不确定度高的像素，增加候选点之间的间距，从而可以评估更大范围的候选点。

Depth consistency weighting(深度一致性权重)

  如果深度假设值式正确的，说明对应的3D点是在物体的表面上，如果这个3D点在邻域视图中可见，那么相应的单视图预预到该深度的概率值应该要高；等价于 “如果从相邻视图估计的深度假设值的单视图深度概率低，则意味着深度候选是错误的或者它在该视图中不可见（例如由于遮挡）”；为此，多视角匹配分数如式5所示：
$$\begin{array}{rl}{s}_{u,v,k}\left(I_t\right)& =\sum _{i\ne t}{w}_{u_{ik},v_{ik},d_{ik}}^{\mathrm{d}\mathrm{c}}⟨{\mathbf{f}}_{u,v}\left(I_t\right),{\mathbf{f}}_{u_{ik},v_{ik}}\left(I_i\right)⟩\\ & \\ w_{u_{ik},v_{ik},d_{ik}}^{\mathrm{d}\mathrm{c}}& =\delta \left(p_{u_{ik},v_{ik}}\left(d_{ik}\mid I_i\right)>p_{\text{thres }}\right)\end{array}\text{\hspace{1em}(5)}$$
其中，当单视图的深度概率 $p_{u_{ik},v_{ik}}\left(d_{ik}\mid I_i\right)>p_{\text{thres }}$ 时， $w_{u_{ik},v_{ik},d_{ik}}^{\mathrm{d}\mathrm{c}}=1$ ,否则等于0，将 $s_{u,v,k}\left(I_t\right)$ 作为深度一致性权重；$p_{\text{thres }}$的设定很重要，太高则会剔除过多的深度候选值（其中可能包含正确的深度值）；文中设 $p_{\text{thres }}=\exp \left(-{\kappa }^2/2\right)/{\sigma }_{u_{ik},v_{ik}}\sqrt{2\pi }$，如果 $d_{i,k}$ 在k-sigma 的置信区间内则会p会趋向于1，$p_{\text{thres }}$是由每个像素与视图共同决定；如果D-Net对于预测深度之不确定（$\sigma$ 很大），则 $p_{thres}$ 很低，可以考虑更多的深度假设值；
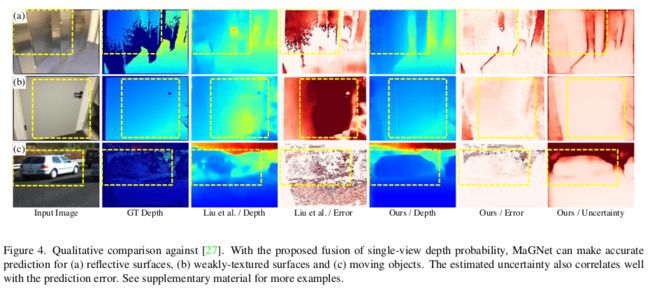
  深度一致性加权可以剔除具有低单视图深度概率的候选深度值。 尤其是当多视图匹配不明确或不可靠时，这种加权方式可以提高模型的鲁棒性。 例如，如果像素位于无纹理表面内，则深度候选范围太广将导致相似的匹配分数。 如果场景包含反射表面，则会在反射之间计算匹配分数，从而导致深度估计过高。 在这两种情况下，MaGNet 都可以通过偏向具有高单视图深度概率的深度候选来进行稳健的预测。

Estimating Multi-View Depth Probability Distribution (多视图深度概率分布估计)

Updating single-view depth probability distribution(更新单视图深度概率分布)

  得益于基于概率分布的深度假设值采样策略，模型得到的匹配代价的维度为 $\frac{H}{4}\times \frac{W}{4}\times N_s$ ，其中 $N_s$ 为深度假设值的数量；将其作为输入，使用 G-Net 更新单视图的均值与方差来估计多视角深度概率分布；由于 ${\mu }_{u,v}$ 和 ${\sigma }_{u,v}$ 没有在输入中编码，很难通过直接回归的方式更新的均值和方差。为此，G-Net采用残差学习的思想，估计均值与方差的归一化残差值$\Delta {\mu }_{u,v}/{\sigma }_{u,v}$。比如当两个像素点的在视差为 $k^{\prime }$ 匹配分数很高时，模型去学习 $b_{k^{\prime }}$ 来更新均值：${\mu }_{u,v}^{\text{new }}={\mu }_{u,v}+b_{k^{\prime }}{\sigma }_{u,v}$。同理，G-Net学习 ${\sigma }_{u,v}^{\text{new }}/{\sigma }_{u,v}$ 来更新方差值；通过这种方式来更新多视图的深度概率分布；注：G-Net 的输出可以反馈到采样模块，并且可以重复该过程以不断优化输出。

Learned upsampling(可学习的上采样)

  G-Net的输出为多视图概率分布图 $\in R^{2\times \frac{H}{4}\times \frac{W}{4}}$，为了将这个概率分布图上采样到原图分辨率，本文提出一个可学习的上采样策略：模型的输入为D-Net的特征图，使用一个轻量化的CNN来预测 $R^{1\times (3\ast 3)\times 4\times 4\times \frac{H}{4}\times \frac{W}{4})}$的mask (4代表与原图的缩放比例) ，将概率分布图$R^{2\times \frac{H}{4}\times \frac{W}{4}}$每个点的$3\times 3$的邻域像素取出来，组成邻域特征图 $\in R^{2\times (3\ast 3)\times 1\times 1\times \frac{H}{4}\times \frac{W}{4}}$ ，将其与mask点乘后在$3\ast 3$ 维度上求和得到$R^{2\times 4\times 4\times \frac{H}{4}\times \frac{W}{4}}$ ，最后resize得到$R^{2\times H\times W}$

def upsample_depth_via_mask(depth, up_mask, k):
    # depth: low-resolution depth (B, 2, H, W)
    # up_mask: (B, 9*k*k, H, W)
    N, o_dim, H, W = depth.shape
    up_mask = up_mask.view(N, 1, 9, k, k, H, W)
    up_mask = torch.softmax(up_mask, dim=2)             # (B, 1, 3*3, k, k, H, W)

    up_depth = F.unfold(depth, [3, 3], padding=1)       # (B, 2, H, W) -> (B, 2 X 3*3, H*W)
    up_depth = up_depth.view(N, o_dim, 9, 1, 1, H, W)   # (B, 2, 3*3, 1, 1, H, W)
    up_depth = torch.sum(up_mask * up_depth, dim=2)     # (B, 2, k, k, H, W)

    up_depth = up_depth.permute(0, 1, 4, 2, 5, 3)       # (B, 2, H, k, W, k)
    return up_depth.reshape(N, o_dim, k*H, k*W)         # (B, 2, k*H, k*W)

Iterative refinement and network training(迭代优化与模型训练)

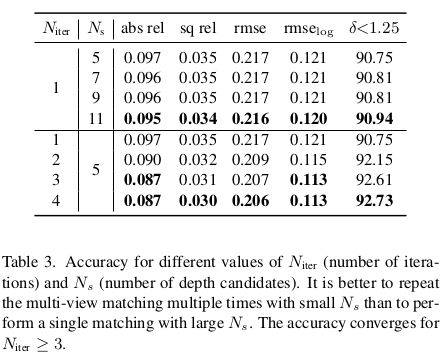
  通过多次重复迭代 $N_{iter}$ 次多视角匹配过程（基于概率分布的深度假设值采样——>多视图一致性权重匹配——>通过G-Net更新概率分布参数）可以得到 $N_{iter}$ 个预测结果；在每次迭代中计算式2的NLL损失，每次迭代计算得到的NLL损失乘以 ${\gamma }^{N_{\text{iter }}-i}$ (后面的权重大于前面的)，这些损失的总和用来训练G-Net与可学习的山采样模块；
  这种迭代的策略有两个好处： (1)如果在某一次迭代过程中，某个像素点的匹配分数较高，那么深度假设空间的均值会向该像素的预测深度值聚拢且方差会减小，那么在下一次的迭代过程中会在上一次的最价值附近寻找深度假设空间，这样可以带来更高的匹配分数；(2)迭代更新还可以防止D-Net预测不准确时导致模型坍塌，比如某像素点的Ground True不再初始的深度假设空间的搜索范围$[{\mu }_{u,v}-\beta {\sigma }_{u,v},{\mu }_{u,v}+\beta {\sigma }_{u,v}]$内,没有任何一个候选的深度值可以得到很高的匹配分数，这种情况下G-Net会通过减小式2的NLL损失值来得到更大的方差值，在下一轮的迭代中可以在更宽的范围内寻找深度值；

---

实验结果