【论文阅读】ZebraPose: Coarse to Fine Surface Encoding for 6DoF Object Pose Estimation
一篇CVPR2022的文章,心血来潮记录下自己的笔记。
论文链接
论文主体内容
本文主要解决6D位姿预测中建立图像(2D)到3D的对应关系的问题
发展情况:sparse templates → \to → deeply learned dense maps → \to → learning object fragments as segmentation
本文提出一个discrete descriptor能够densely represent the object surface,用多层次binary grouping来编码物体表面信息,然后提出一个coarse to fine的训练过程,用以产生细粒度的预测,最后用PnP方法将预测的编码和物体表面进行匹配进而得到6D位姿。
现有方法:
-
早期的位姿预测问题上,深度图通常用于辅助建立图像像素点到三维点的对应关系,但是获取深度图、利用深度图是一个比较棘手的问题。
-
随着深度学习和CNNs的发展,抛弃深度图来进行位姿估计成为可能
-
Perspective-n-Points (PnP) 算法需要至少4个2D-3D的匹配点对才可以进行下去,这样的sparse method是寻找一部分关键点来进行位姿估计
问题是无法解决视点变动、遮蔽、纹理缺失的问题
-
深度神经网络可以用于图像合成,利用图像合成技术可以生成dense correspondence maps
问题是神经网络通常产生的是平滑(smooth)图像,损失了一些底层的几何信息
-
-
可以看出上述方法在建立2D到3D的对应关系的时候,图像像素点不一定能和物体表面直接对应,即可能一些点在物体有在图片里没有,一些点在图片里有在物体上没有
本文贡献:
- 考虑到神经网络在分类问题上的优秀表现,本文将handcrafted features和多层次的image segmentation两种思想结合起来用以基于RGB的位姿估计,通过多层次的离散表示,在保证compact mapping的同时把学习目标转化为了多标签分类问题
- 又考虑到一次性编码整个序列比较受限,本文提出了coarse to fine的训练框架,在coarse level的编码结果可以在更宽的物体区域上共享,当网络学会区分coarse splits的时候在去进一步聚焦于finer position
- 本文的编码方式建立的是putative correspondence,direct pixel-to-surface matching
具体来说,将位姿估计问题分解为以下三步:
- 对每一个三维点都安排一个独一无二的descriptor
- 预测2D像素点到3D点的dense correspondence
- 用对应关系来解决位姿估计问题
Coarse to Fine Surface Encoding
给定一个物体的CAD model和该物体的顶点 v i v_i vi ,现在要给这个顶点以独一无二的编码 c i c_i ci ,编码长度为 d d d ,这个编码肯定不能随便定义,它既要考虑到这个顶点在物体表面的位置,也要能够支持coarse to fine的学习过程。
用低进制的数字系统(如二进制)能让representation更加高效,提供更简单的从coarse到fine的分组,比如十进制会在迭代时分成10组用0-9表示,但是二进制只需要分成2组分别用0和1表示
本文提出的编码方式有点像霍夫曼编码,区别就是本文的编码方式是从上到下进行的。

G j G_j Gj 代表第 j j j 次迭代时产生的 r j r^j rj 个group的集合,其中 j ∈ { 0 , 1 , ⋯ , d } j\in\{0,1,\cdots,d\} j∈{0,1,⋯,d}
G 0 G_0 G0 是初始化的group,包含了全部顶点,在接下来的每一次迭代过程 j j j 中,都将前一次的集合 G j − 1 G_{j-1} Gj−1 中的每一个group再细分成 r r r 个group,直到切分停止
在上述的过程中,在 G j G_j Gj 的group g k ( k ∈ { 0 , ⋯ , r − 1 } ) g_k(k\in\{0,\cdots,r-1\}) gk(k∈{0,⋯,r−1}) 里有一些顶点,这些顶点在编码的第 j j j 位的数字就是 k k k ,举例来说,如果某个顶点在每次切分后都属于r个group的第0个group,那么它的编码就是 v = { 0 , 0 , 0 , ⋯ , 0 } v=\{0,0,0,\cdots,0\} v={0,0,0,⋯,0} 共 d d d 位。
如何选取基数 r r r ?
从上面编码的方式来看,最终的切分结果集合 G d G_d Gd 共有 k = r d k=r^d k=rd 个group,也就是说我们如果要对某个顶点进行分类的话,会有 k = r d k=r^d k=rd 个类。
那么在神经网络里如何能表示出这 k k k 个类呢?假设在第 d d d 层的网络中,输入group(属于同一次迭代的所有group都视为同等地位的输入,经过同一层网络得到输出),输出 r r r 个分组,那么整个神经网络就会产生 o = r ⋅ d o=r\cdot d o=r⋅d 个输出。
这里我就产生了一个问题,显然网络的每层都相当于是单独接收输入产生输出,那么是否相当于丢失掉了前面的分组信息?
想要网络的output个数 o o o 尽可能少(方便训练),同时让类尽可能的多(更加细粒度),则有 o m i n = min r ( r ⋅ d ) = min r ( r ⋅ log r k ) = 2 ⋅ log 2 k o_{min}=\mathop{\mathrm{\min}}\limits_{r}{(r\cdot d)}=\mathop{\mathrm{\min}}\limits_{r}{(r\cdot \log_rk)}=2\cdot\log_2k omin=rmin(r⋅d)=rmin(r⋅logrk)=2⋅log2k ,即 r r r 的最优正整数选择为2,此时对于每个要切分的group,只需要将这个group的每个顶点做二分类即可。此时网络共有 log 2 k \log_2k log2k 层。
其实这里 r r r 的最优解为2或4,但是考虑到网络产生2个输出时不需要使用交叉熵损失函数,所以选择了2。
为什么不用交叉熵呢,因为神经网络的输出只有两个,如果已知第一个输出的概率,那么第二个就直接确定了,但是如果有三个输出的话,已知第一个是没办法得到后面两个的。
Rendering the Training Labels
这里是为了产生训练数据,对于一个物体来说,它的每个顶点的编码都是独一无二的,编码的某一位代表了在某次迭代中所属的group,即每一位都是做r分类的结果,记为class id。
那么当我们知道了某个顶点的编码后,对于一张图片,我们要做的就是对图片中物体所在的每一个像素去预测它对应哪个顶点,即预测图片中像素对应的顶点编码,显然这在训练数据里是没有的,想要生成训练数据,就需要得到多组(n个像素的图片和这n个像素对应的编码)这样的数据,现在已经得到了顶点的编码,所以只需要渲染物体在多个位姿下对应的二维图像,那么图像中出现的顶点对应的编码就是groudtruth。
这里我又产生了一个问题,这样渲染出来的图片肯定是只有物体、黑色背景且光照、纹理条件一致的,那么对现实世界图片的泛化性就会很差
但是每个点映射下去肯定是不连续的,而我们想要生成连续的图片而不是点构成的散点图一样的图片,所以点的编码就需要转换成网格化面的编码(关于网格化面可以去看这个:三角网格和四边形网格),具体做法是:
- 如果一个网格化面的两个顶点同属于一个分组,那么这个面就对应这个class id
- 如果一个网格化面的顶点属于不同的分组,那么这个面的class id就是面的第一个顶点的class id
- 不断重复上述过程直到 d d d 位编码都产生完毕。
网络结构
在上面的内容里说过,神经网络用作分类器来产生输入图片每个像素对应的顶点编码,那么对于输入的图片来说,它的大小肯定是统一的 H × W H\times W H×W ,随之而来的问题就是图片中有一部分像素并不是物体,不是物体的显然就不需要去预测顶点编码,所以肯定需要mask来把物体的部分标出来。
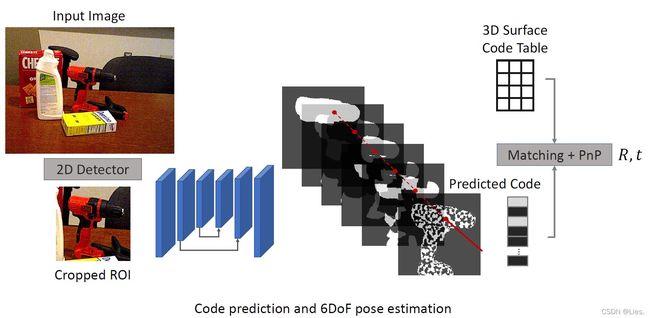
既然前面的工作都是对一个像素点进行分类得到编码,那么与其单独的去处理图片的mask,不如在编码里加一位,让这一位来决定这个像素是或不是物体,也恰好是个二分类,和 r = 2 r=2 r=2 十分契合。
按照上面的思路,网络就会产生 d + 1 d+1 d+1 个输出作为像素的编码,在预测过程中网络不会输出整数,而是输出一个0-1之间的概率,将这个概率进行四舍五入就能得到整数编码。
一帧图像中可能会有多个物体,所以用一个2D detector检测多个RoI,那么对于每帧图片,实际就是个多标签分类任务
层次化学习
直接从像素来得到和三维点的对应关系无疑是一个细粒度的任务,而神经网络更常用于coarse level prediction,也就是说在某个小范围内,由每个像素得到的特征是十分相似的,所以本文提出了一个coarse to fine的方式学习到更细粒度的任务,在每个层次的每个位置上使用误差直方图 (error histogram) ,然后利用给定的error为Hamming-based loss加权,进而实现coarse to fine。
-
Mask Loss,这个就不多说了,把预测得到的概率通过一个sigmoid function,然后用 L 1 L_1 L1 loss作为 L m a s k L_{mask} Lmask
-
Hamming distance, H a m m ( b , p ^ ) = ∑ j = 1 d [ b j log p ^ j + ( 1 − b j ) log ( 1 − p ^ j ) ] Hamm(b,\hat p)=\sum_{j=1}^d\bigl[b_j\log \hat p_j+(1-b_j)\log (1-\hat p_j) \bigr] Hamm(b,p^)=∑j=1d[bjlogp^j+(1−bj)log(1−p^j)]
对于一个RoI,网络输出 d × H × W d\times H\times W d×H×W 的概率图 p ^ \hat p p^,然后将其四舍五入得到每个像素点对应的编码图 b ^ \hat b b^,编码的groundtruth是 b b b,上面这个形式其实就是二值交叉熵损失函数, j j j 代表编码位数。
-
Active bits,激活字节,因为编码的低位对应coarse correspondence,高位对应fine estimates,所以在训练的初始阶段,网络更聚焦于学习编码低位对应的特征,在编码高位上的误差就比较大,但是就算高位上误差较大,低位上的划分也是正确的,这个时候如果单纯的把它看作错误也肯定是不对的。
因此通过每个编码位的误差直方图来对编码低位进行加权:
在时刻 t t t ,编码的每个字节对应的直方图为 H j ( t ) = a v g ( λ ( b j t − b ^ j t ) + ( 1 − λ ) ( b j t − 1 − b ^ j t − 1 ) ) H_j(t)=avg\bigl(\lambda (b_j^t-\hat b_j^t)+(1-\lambda)(b_j^{t-1}-\hat b_j^{t-1})\bigr) Hj(t)=avg(λ(bjt−b^jt)+(1−λ)(bjt−1−b^jt−1))
-
Hierarchical loss
在某时刻 t t t,通过每个字节的误差直方图可以对各个字节进行加权,来决定当前时刻聚焦于哪个字节(聚焦于低位对应的coarse阶段还是高位对应的fine阶段),每个字节的在当前时刻对应的权重为 w j ( t ) = exp ( σ ⋅ min { H j ( t ) , 0.5 − H j ( t ) } ) w_j(t)=\exp(\sigma \cdot \min\{H_j(t),0.5-H_j(t)\}) wj(t)=exp(σ⋅min{Hj(t),0.5−Hj(t)}) ,然后将所有字节的权重归一化,结合Hamming distance就能得到本文所使用的Hierarchical loss:
L h i e r = ∑ j = 1 d w j ⋅ H a m m ( b j , p ^ j ) L_{hier}=\sum_{j=1}^dw_j\cdot Hamm(b_j,\hat p_j) Lhier=∑j=1dwj⋅Hamm(bj,p^j)
从权重的表达式可以看出来,误差过小或过大的字节都会被赋予比较低的权重,能使网络聚焦于当前的字节,所以把权重大的定义为active bits -
至此,得到总的损失函数 L t o t a l = L m a s k + α ⋅ L h i e r L_{total}=L_{mask}+\alpha\cdot L_{hier} Ltotal=Lmask+α⋅Lhier
pose estimation
这个阶段基本就是引用现有的方法了,只是把匹配过程中用到的templates换成了自己设计的,这里放一段原文
For the matching, we use a lookup table that extracts the corresponding 2D and 3D points. Following that, we use Progressive-X solver to calculate the rotation R R R and translation t t t.
实验部分
-
数据集:
LM-O,LM的recall已经被提的非常高了,所以用更有挑战性的LM-O数据集,但是LM-O的训练图片很少,一些现有的方法是利用合成图片(physically-based rendering)进行训练,本文既用了数据集的也用了pbr合成的。
YCB-V,一个很有挑战性的数据集,因为训练图片中的物体几何对称,且有大量遮挡。
- 实验细节:
取 $k=256^2=2^{16}=65536$ ,因此将三维模型不断划分直到拥有超过65536个顶点。
改进k-means聚类算法,保证不出现在未迭代完时有的group少于两个顶点无法继续向下划分的情况。
改进**Deeplabv3**,在其中添加了skip connections,用**Resnet34**作为主干网络。在训练过程中与**CDPN**采用相同的策略(dynamic zoom-in strategy)来给RoI增加噪声。
input RoI会resize成 $256\times 256\times 3$,output的宽和高均为128,$\lambda=0.05,\sigma=0.5,\alpha=3$,训练380k个step,batch size为32,lr为2e-4,bounding box由**CDPNv2**提供。
由于顶点代码中任何位的变化都将直接指向另一个顶点,它甚至可能指向另一侧的一个顶点。为了由groundtruth correspondence map呈现的拓扑结构,我们在生成groundtruth时禁用了插值。但是在实际训练阶段,插值其实也做到了,是在resize的时候以最近邻插值形式做到的。
- 评价指标:ADD,计算了模型在预测的位姿下投影到camera domain和模型在groundtruth位姿下投影到相机坐标系的点的平均距离。对对称物体来说, ADD-S计算的是groundtruth位姿下匹配的最近的模型点来来代替ADD里的后者。
如果ADD(-S)的误差小于物体直径的10%,则认为预测的位姿是正确的。
对YCB-V,ADD(-S)的AUC(area under curve)也是评价指标,阈值为10cm
- LM-O
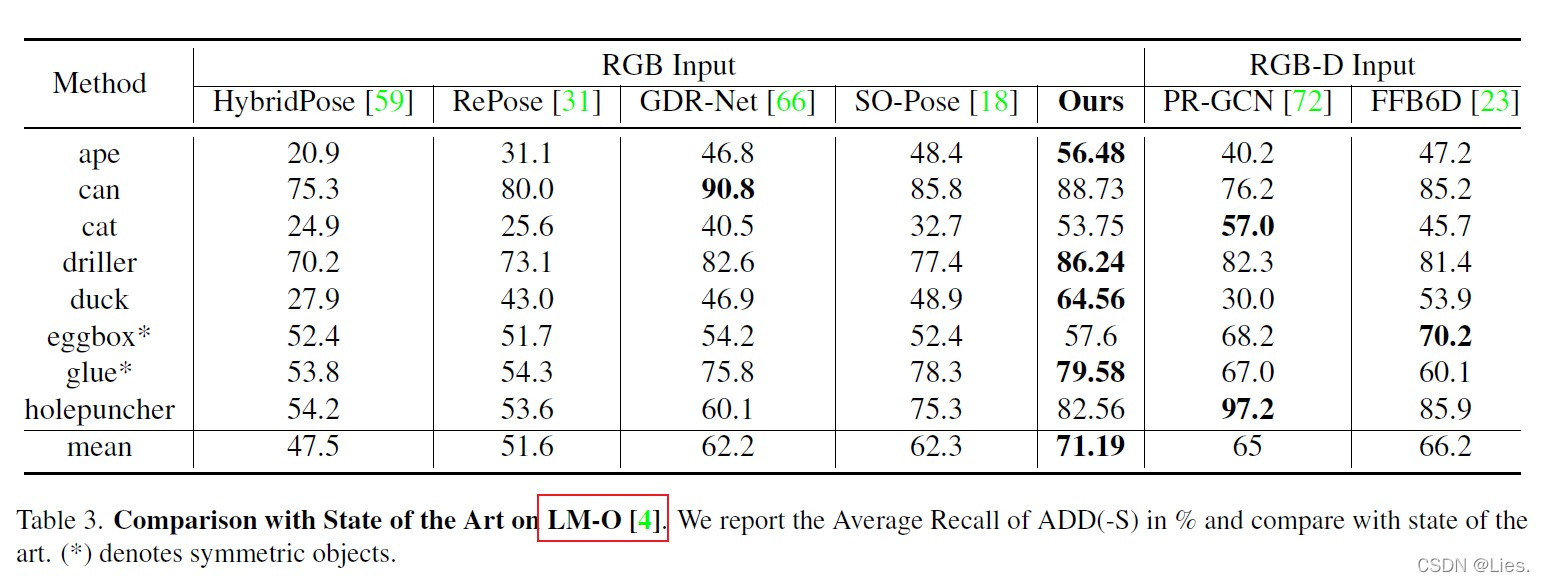
本文提出的方法在最终结果上超过了所有基于RGB的现有方法,甚至超过了基于RGB-D的方法,LM-O数据大多数都是无纹理的,意味着RGB-D方法有天然的优势,尽管如此本文的方法也优于他们。
- YCB-V
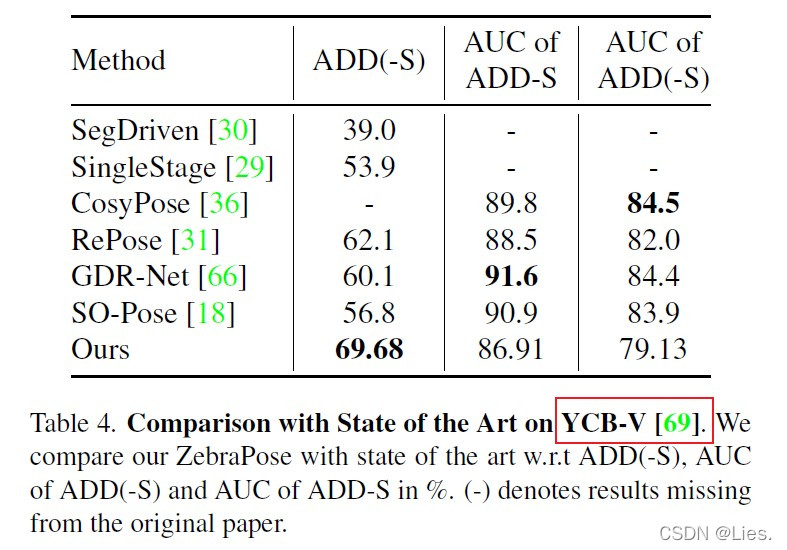
本文的方法在ADD(-S) metrics上的表现远优于其他方法,但是在AUC的表现上欠佳,主要是因为ADD(-S)的误差阈值大概为2cm,而AUC的误差阈值为10cm,也就意味着本文的方法能够预测更加精确的位姿,而其他方法在粗略的估计上更有优势。
- 消融实验
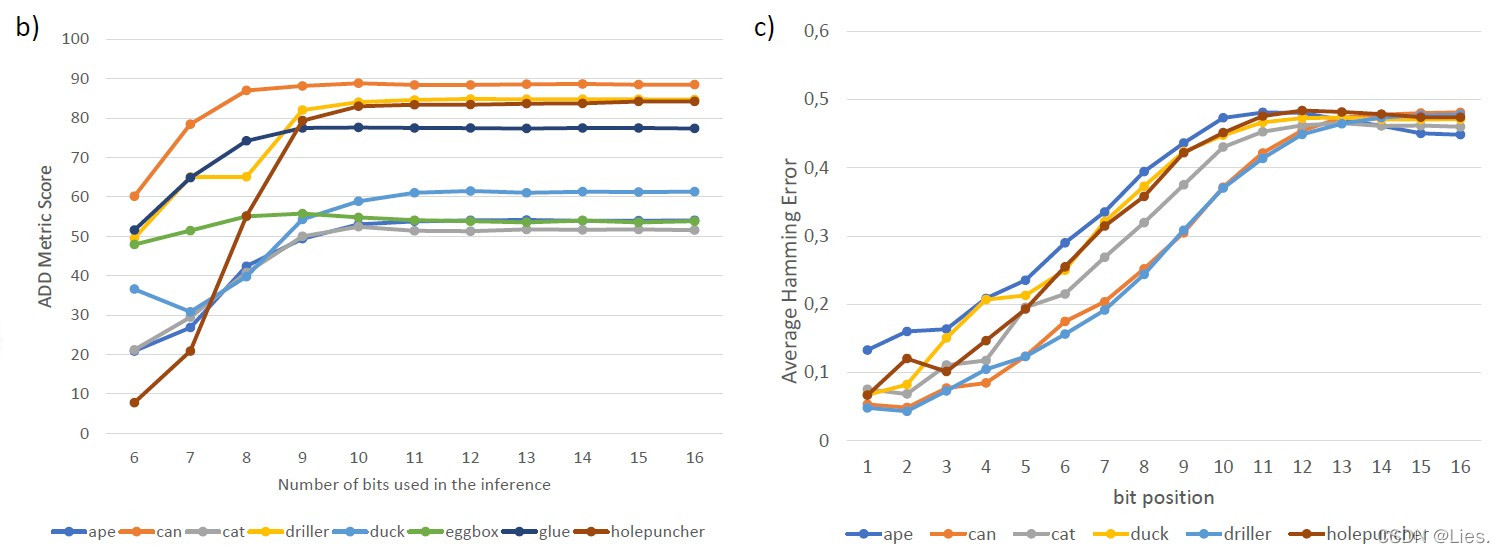
左图是仅使用前 $j$ 位编码对ADD(-S)进行测试的结果,可以看出编码位数不断增加后性能会趋于不变,也就是说更多的编码位数可能会产生冗余,这个也很好理解,更多的编码位数代表我们在分割模型的时候分的更细,就会出现某些编码不同的顶点在渲染成图片的时候会落在同一个的像素上,这显然是冗余的。
右图编码中各个字节位上的平均误差率
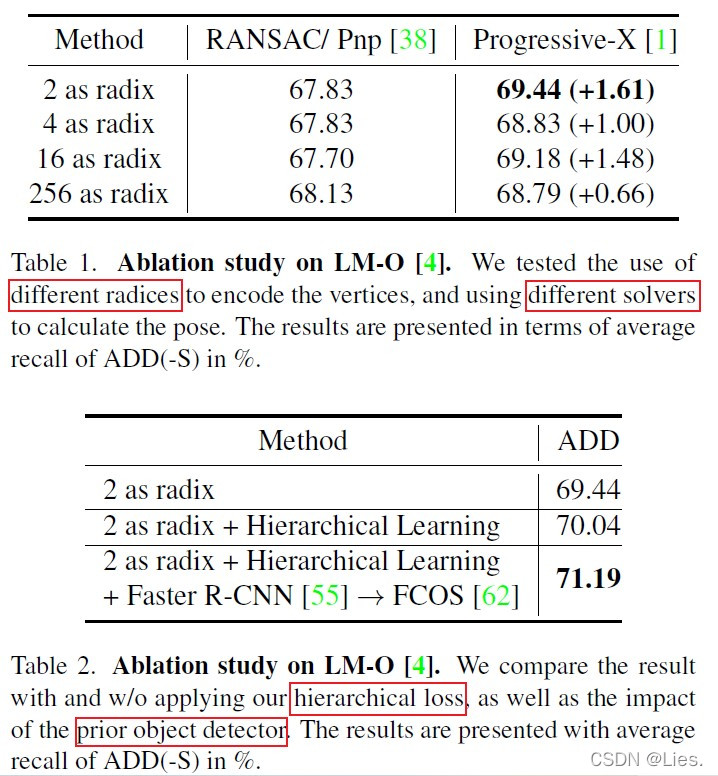
Table1是不同的基数 $r$ 和不同的pose eatimation方法对ADD(-S)的影响,可以看出对RANSAC/PnP来说不同的 $r$ 影响不大,而Progressive-X用更小的 $r$ 会明显提高。
> Progressive-X包含**spatial coherence filter**,可以根据2D correspondence检查其周围的3D点。如果绝大多数的预测都是正确的,那么其周围的点也基本都落在某个领域内,如果某个点预测错误,那么就可以从周围的点判断出来它是个outlier。
但是Progressive-X无法检测出最后一些字节位的错误,所以从各个字节位的平均误差率的图里也可以看出来最后几个字节的误差率较高。
Table2是多层次训练的有效性和产生bounding box的方法的影响,结果很明确,不再赘述。
论文主体内容到此就阅读完毕,还有几个不懂的地方,基本都是一些没有涉猎过的方法:
- UV or UVW values in object local coordinates
- binary-based descriptors, in ORB and SLAM
- Deeplabv3
- Resnet34
- CDPN and CDPNv2
- Progressive-X
还需要读相关论文了解上面这些东西的思想。