Unsupervised Monocular Depth Estimation with Left-Right Consistency 论文笔记
Unsupervised Monocular Depth Estimation with Left-Right Consistency
论文链接: https://arxiv.org/abs/1609.03677
Problem Statement
这是一个双目自监督深度估计的论文,利用两张图片进行深度估计,但是在推理阶段可以使用一张图片进行深度估计。利用对级几何约束,把深度估计当成是图像重构的问题。但是仅仅是图像重构会导致较差的深度估计结果,因此作者提出了一个新的training loss。
Direction
因为把单目深度估计问题当成是image reconstruction 问题, 仅仅是最小化 photometric loss的结果是有好的图像重构结果,但是深度质量较差。新的training loss加强了在左右视图之间差异的consistency,从而提高了性能和鲁棒性。
Method
一、Depth Estimation as Image Reconstruction
本质上,给定一个标定后的双目相机,如果可以学习到一个函数,这个函数可以从另外一张图片重构一张图片,就可以进行场景的三维成像。
所以在训练的时候,给定两张图片 I l I^l Il和 I r I^r Ir, 作者没有直接用这两张图像进行深度估计,而是尝试去找dense correspondence field d r d^r dr, 当把这个dense correspondence field应用于左图像的时候,能够使得我们重构出右图像。因此,我们把重构出来的图像 I l ( d r ) I^l(d^r) Il(dr)标记为 I r ^ \hat{I^r} Ir^。同理也可以给定右图像,重构出左图像 I l ^ = I r ( d l ) \hat{I^l}=I^r(d^l) Il^=Ir(dl)。 d d d 对应的就是图像的差异— 网络模型去预测每个像素的一个scalar value。然后给定了相机的baseline b b b 和 focal length f f f, 就可以根据下面公式计算出深度 d ^ \hat{d} d^
d ^ = b f / d \hat{d} = bf/d d^=bf/d
二、Depth Estimation Network
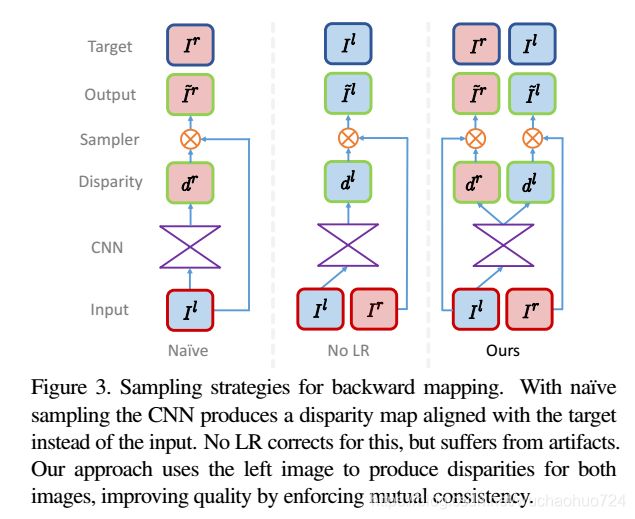
网络通过推断改变左侧图像以匹配右侧图像的差异来估计深度。这个方法的关键是,我们可以只使用左输入图像同时推断两个差异(从左到右和从右到左),并通过强制它们彼此一致来获得更好的深度。
可以看到上图有三个例子,第一个只输入一张图片,经过CNN后获得dense correspondence field,然后把这个应用于原始图片(左图),获得重构出来的右图 I r ^ \hat{I^r} Ir^。我们希望输出的重构图与输入的左侧图像对齐 I l ^ \hat{I^l} Il^,这意味着网络必须从右侧图像采样。因此有了上图中间那个。但这个方法有个问题就是: 视差会"texture-copy" 和 深度不连续的误差。所以为了解决这个问题,作者提出了对两个图进行预测。值得注意的是,训练的时候需要两张图片输入,而推理的时候只需要左图。网络结构是一个encode和一个decoder。
三、 Training Loss
整个loss是:
C = ∑ s = 1 4 C s C=\sum_{s=1}^4 C_s C=s=1∑4Cs
其中 C s C_s Cs 主要有三项组成:
C s = α a p ( C a p l + C a p r ) + α d s ( C d s l + C d s r ) + α l r ( C l r l + C l r r ) C_s = \alpha_{ap}(C_{ap}^l + C_{ap}^r) + \alpha_{ds}(C_{ds}^l + C_{ds}^r) + \alpha_{lr}(C_{lr}^l + C_{lr}^r) Cs=αap(Capl+Capr)+αds(Cdsl+Cdsr)+αlr(Clrl+Clrr)
Appearance Matching Loss
C a p C_{ap} Cap是使得重构的图片相似于输入图片。网络在训练的时候,对相反的双目视图进行采样像素(左->右,右->左)。而作者使用的是 bilinear sampler是局部完全可微的,并且无缝地集成到我们的完全卷积结构中,这意味着我们不需要任何cost function的简化或近似。也使用L1 loss和 single scale SSIM的组合作为photometric inmage reconstruction cost。
C a p l = 1 N ∑ i , j α 1 − S S I M ( I i j l , I i j l ) ^ 2 + ( 1 − α ) ∣ ∣ I i j l , I i j l ) ^ ∣ ∣ C_{ap}^l = \frac{1}{N} \sum_{i,j} \alpha \frac{1-SSIM(I_{ij}^l, \hat{I_{ij}^l)}}{2} + (1-\alpha) ||I_{ij}^l, \hat{I_{ij}^l)}|| Capl=N1i,j∑α21−SSIM(Iijl,Iijl)^+(1−α)∣∣Iijl,Iijl)^∣∣
上面的公式比较了输入图片和输出的重构图, N N N是像素的数量。
Disparity Smoothness Loss
C d s l = 1 N ∑ i , j ∣ ∂ x d i j l ∣ e − ∣ ∣ ∂ x I i j l ∣ ∣ + ∣ ∂ y d i j l ∣ e − ∣ ∣ ∂ y I i j l ∣ ∣ C_{ds}^l = \frac{1}{N} \sum_{i,j}|\partial_x d_{ij}^l|e^{-||\partial_x I_{ij}^l||} + |\partial_y d_{ij}^l|e^{-||\partial_y I_{ij}^l||} Cdsl=N1i,j∑∣∂xdijl∣e−∣∣∂xIijl∣∣+∣∂ydijl∣e−∣∣∂yIijl∣∣
因为深度不连续通常发生在image gradients处,作者在disparity graidents ∂ d \partial d ∂d 使用 带edge-aware term 的L1 loss。能够smooth disparity。
Left-Right Disparity Consistency Loss
为了保证连贯性, 使用了 L1 left-right disparity consistency penalty。这个cost尝试使得左视角的视差图等于重构出来的右视角视差图。
C l r l = 1 N ∑ i , j ∣ d i j l − d i j + d i j l r ∣ C_{lr}^l = \frac{1}{N}\sum_{i,j}|d_{ij}^l - d_{ij+d_{ij}^l}^r| Clrl=N1i,j∑∣dijl−dij+dijlr∣
Conclusion
在occlusion boundaries上表现不好,因为在重叠出左右视图都看不到,对于镜面和透明的表面会产生不连续的深度(specular and transparent),而且训练的时候需要两个视角的输入图像,比较麻烦。
Reference
- https://arxiv.org/abs/1609.03677