Radon 变换原理和应用
Radon 变换原理和应用
前言: 承接 Hough 变换,从简单的直线检测说起,推广到 Radon 变换。介绍了 Radon 变换的基本原理和应用。主要是Hough直线检测的拓展,深度较浅。
上启自:详解 Hough 变换
文章目录
- Radon 变换原理和应用
-
- 1. 从直线检测说起
-
- 1.1 基本问题
- 1.2 另辟蹊径
- 1.3 编程实现
- 2. Radon 变换
-
- 2.1 回顾
- 2.2 Radon 变换
- 2.3 Radon 逆变换
- 3. 应用
1. 从直线检测说起
1.1 基本问题
在 详解 Hough 变换 中,对直线检测折腾这么久,已经是个成熟的”直线检测者”了,所以基本问题就不从点分析,直接从图出发。即
如何检测下图(a)中的直线?
再简单概述下原理:即,将原空间中的点变换到参数空间,每个原空间的点对应参数空间一条直线。原空间中有N个点就对应参数空间中N个直线。参数空间中直线相交就是表明对应原空间的点共线。参数空间中交点重复次数(亮度)越多,就表明原空间中共线的点越多。这些点连起来就是要求的直线。
注:如果使用 Hough变换 博文中的代码,将 θ \theta θ 范围修改下,其实不必 [ 0 , 2 π ] [0,2\pi] [0,2π],修改为 [ 0 , π ] [0,\pi] [0,π] 即可。
1.2 另辟蹊径
检测之前一般都是进行边缘提取,我们的目标是检测 图(b) 边缘二值图中是否存在直线,以及,如果存在,表示出这条直线。
先抛弃 Hough 变换的思路,考虑另外想法。
(1) 第一种想法:考虑从不同方向把 (b) 图拍扁(术语叫投影)。比如从两个角度(下图 A 1 , A 2 A1,A2 A1,A2 )拍扁(投影)它,示意如下:
这里使用两个方向 ( α = 0 \alpha=0 α=0 和 α = 45 ° \alpha=45° α=45° )的光线 A 1 , A 2 A1,A2 A1,A2 对边缘进行投影。假设投影到投影面的位置点的数量越多,投影结果越亮。那么图中,灰色箭头标志的地方会非常亮。因为整条直线的像素点都会投影到该处。
不仅如此,事实上,考察所有投影方向,即 α ∈ [ 0 , π ] \alpha\in [0,\pi] α∈[0,π] (注意:因为不分正负,所以 [ 0 , π ] [0,\pi] [0,π] 和 [ π , 2 π ] \pi,2\pi] π,2π] 结果是一样的),最亮的点依旧会是图示中灰色标志的部分。这是直线的特点。
所以,是否我们可以考察所有方向下,对边缘图像进行投影,找到最亮的点(或者达到规定亮度阈值的点,比如存在多条直线)和此时对应的光线方向。 那这条直线不就检测出来了,直线方程不就确定了吗?
先不着急编程实践,再思考另一种想法。
(2)第二种想法:Hough 变换中,有提到可以用 θ \theta θ 和 d d d 表示一条直线,如下图示意(不懂为何,可以参考 Hough 变换博文):
其中, d d d 为圆心到直线距离, θ \theta θ 是垂线与 x x x 轴夹角。那么这一想法就是使用 穷举法 的思想,即
因为 θ \theta θ 是有范围的,同时因为在图像中检测直线,所以 d d d 也是有范围,最大为图像的斜对角距离。于是,我们就考察“所有”的 θ \theta θ 和 d d d ,这里的”所有“取决于你的精度,即 θ \theta θ 以及 d d d 各自的离散值取值间隔。来表示图像空间内”所有“的直线。
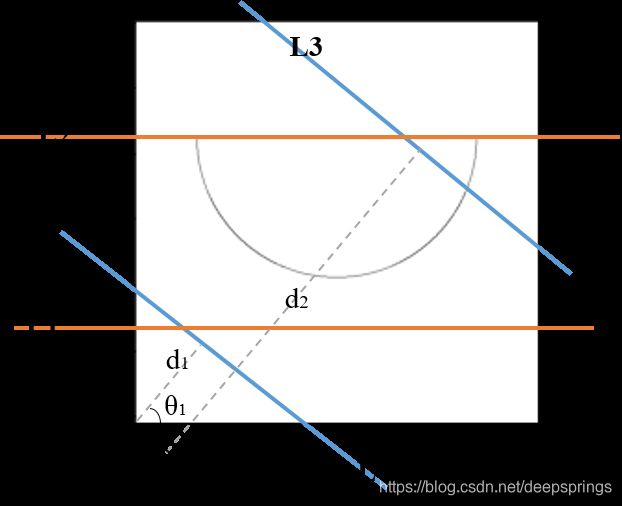
表示出”所有“直线后,下面我们要做的就是,将直线一条一条的与原图相匹配。记录该直线的点与边缘图中点重叠的个数,把该个数记为该线与图的匹配度。比如取所有线的其中四条,作个示意:
其中, L 1 , L 2 L1,L2 L1,L2 和 L 3 , L 4 L3,L4 L3,L4 故意取了 θ \theta θ 相同,但 d d d 不同所表示的直线(图中L1,L2没有标角度和距离,怕线看起来太乱了)。上面所说的匹配度即该条直线与边缘图中像素重叠数,如 L 1 L1 L1 与 边缘线没有像素重叠,匹配度就为0, L 4 L4 L4同理。其中这举例的四条直线中,匹配度最高的是 L 2 L2 L2。因为它与边缘图中包含直线的所有像素都重合。
不仅如此,事实上,考察所有 θ \theta θ,距离 d d d 所表示的直线,匹配度数值最高的依旧会是 L 2 L2 L2。
说到这,你可能会发现,其实这就是所提到的第一种想法的另种思路。只是这里的 L 1 , L 2 , ⋯ L1,L2,\cdots L1,L2,⋯ 就是第一种想法中的 一条 光线,如 第二种想法里的 L 2 L2 L2 直线其实就是 第一种想法里 A 2 A2 A2 方向下,最亮点对应的那一条光线。匹配度也就对应于第一种想法里的亮度,也就是重合度。
唯一的区别和需要注意的是,两个想法中的所用角度表示方法不同(但属于无伤大雅的东西):前者是光线的倾角,后者是光线垂线的倾角。
1.3 编程实现
基于以上想法,编程,进行直线检测:
注:这里使用想法二中的倾角 θ \theta θ,这一倾角的好处和直线表示方法,参看Hough变换博文。
直接给出结果,通过 θ \theta θ 和 d d d 确定的直线方程为
d = x c o s θ + y s i n θ d = xcos\theta+ysin\theta d=xcosθ+ysinθ
完整代码如下:
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图片
imgPath = "C:\\Users\\zhangwei156\\Desktop\\figure\\waterm.jpeg"
grayImg = cv2.imread(imgPath, 0)
# 提取边缘
edgeImg = cv2.Canny(grayImg, 300, 500)
H, W = edgeImg.shape
# 精度
theta_div = 500
d_div = 500
theta_max = np.pi
dMax = np.floor(np.sqrt(H**2 + W**2))
# 离散取值
theta = np.linspace(0, np.pi, theta_div)[:-1]
d = np.linspace(-dMax, dMax, d_div)
# 分辨率
theta_res = np.pi/(theta_div-1)
d_res = 2*dMax/(d_div-1)
# 记录 亮度/匹配度/叠加次数 的模板
forceImg = np.zeros((theta_div, d_div), np.uint16)
mesh = np.meshgrid(theta, d)
for _t, _d in zip(mesh[0].flatten(), mesh[1].flatten()):
# 分母为 0 情况
if _t == 0:
continue
y = np.arange(0, H)
x = y * 0 + 1
else:
x = np.arange(W)
y = ((_d-x*np.cos(_t))/np.sin(_t)).astype(np.int64) # theta 和 d 确定的直线
pixel = 2 # 上下容错像素范围
# y轴上下容错像素
for i in range(1, pixel+1):
x = np.hstack((x,x,x))
y = np.hstack((y-i,y,y+i))
# 剔除 y < 0 和 y > H 也即图像外的点
ind = np.where( (y>=0) & (y<H) )
if ind[0].shape[0] == 0:
continue
y = y[ind[0]]
x = x[ind[0]]
index = np.where(edgeImg[y, x]!=0 )[0]
# 取值
tt = int(_t/theta_res)
dd = int((_d+dMax)/d_res)
# 亮度值
forceImg[tt, dd] = index.shape[0]
# 结果
plt.imshow(forceImg)
plt.show()
# 检查结果正确与否的代码
# 最亮处所代表的 theta 和 d 值
O = np.where(forceImg == np.max(forceImg))
# theta 和 d 的真实值
theta_ = O[0]*theta_res
d_ = O[1]*d_res - dMax
# 在原图中显示检测到的直线
for _o in (zip(theta_, d_)):
x_ = np.arange(W)
y_ = ((_o[1]-x_*np.cos(_o[0]))/np.sin(_o[0]))
ind_ = np.where((y_>0) & (y_<H))
x_ = x_[ind_[0]]
y_ = y_[ind_[0]]
plt.imshow(grayImg)
plt.plot(x_,y_,color = "r")
plt.show()
结果展示:
其中, f o r c e I m g forceImg forceImg 中最亮点对应的实际 ( θ , d ) = ( 1.561 , 181.383 ) (\theta, d) = (1.561, 181.383) (θ,d)=(1.561,181.383) ,即 θ = 89.46 ° ; d = 181.4 \theta = 89.46° ; d=181.4 θ=89.46°;d=181.4 。看来垂线还不是纯竖直的,有一点点偏。
此时,你会有个很“吃惊”的发现。
对比一下前面展示的使用 Hough 变换方法时结果,两者 f o r c e I m g forceImg forceImg 图是一致的!
想象一下整个过程,实际上,针对上述问题,它就是 Hough 变换的解决方式。它就是 Hough 变换。
换句话说,想法一,想法二以及之前的 Hough 直线检测想法都是同源的!
区别在于:Hough 变换中使用 θ , d \theta,d θ,d 穷举的是过每个边缘点的所有直线,而以上两个想法通过 θ , d \theta,d θ,d 穷举的是图像空间内所有直线。但 Hough 变换有基于先验知识,换句话说,Hough变换更精准。
所以之后用 Hough 检测直线时,也可以使用 randon 变换函数(上面这个就是最基础的randon变换,就是后面要引申的本文主题,但这里不得不先提下)。
2. Radon 变换
2.1 回顾
回顾上述过程,从某个方向对图像投影,一个特定的 θ , d \theta,d θ,d 确定某条唯一的光线,投影结果为一个固定值,即亮度(累加度)。也即 ( θ , d ) ⟶ 亮 度 (\theta,d) \longrightarrow 亮度 (θ,d)⟶亮度 ,这是个函数对应关系。
亮度的计算是光线对应图像上的像素值累加。上例的特殊之处在于,边缘图为二值图,即边缘部分像素值为 1,黑色部分像素值为 0。
想象若图像像素值为任意值,事实上也可以累加。推广到更一般情况,即不再如图像像素那般是一格格的、离散的,而是连续的。那求和其实就是求线积分。
把问题推广到这种程度,事实上就是要展示的 Radon 变换内容。
2.2 Radon 变换
如下图所示,不再是简单的离散像素,而是连续的函数值 f ( x , y ) f(x,y) f(x,y),我们暂且称之为”密度“。一条由 θ , d \theta,d θ,d 确定的唯一光线,经过 f ( x , y ) f(x,y) f(x,y) 物体,得到亮度值为 R R R 的投影。
根据以上的思路,此时亮度值应该是 L L L 线积分,即
R = ∫ L f ( x , y ) d s R = \int_L f(x,y)ds R=∫Lf(x,y)ds
且光线 L L L 可以由 θ , d \theta,d θ,d 唯一确定,即
L ( θ , d ) : d = x cos θ + y sin θ L(\theta,d):\ \ d = x\cos\theta + y\sin\theta L(θ,d): d=xcosθ+ysinθ
也就有
R ( θ , d ) = ∫ L ( θ , d ) f ( x , y ) d s R(\theta,d) = \int_{L(\theta,d)} f(x,y)ds R(θ,d)=∫L(θ,d)f(x,y)ds
该式子也就是一个全新的函数对应关系,表示的是给定自变量 θ , d \theta,d θ,d ,会有与之对应的函数值 R ( θ , d ) R(\theta,d) R(θ,d) ,该值的物理意义为亮度(或者说是叠加度、衰减后的值、匹配度等等)。而 θ , d \theta,d θ,d 为连续的,因此将该函数用图像画出来就是对应于前面 f o r c e I m g forceImg forceImg 的样子,即横、纵坐标为 θ , d \theta,d θ,d,亮度大小为 R R R。更一般情况是对应一个三维空间, x , y x,y x,y 轴为 θ , d \theta,d θ,d , z z z 轴对应为 R R R。
下面就是对积分的计算,该部分为数学中线积分求解问题,不详述。
法一:直接求解
当给定 θ , d \theta,d θ,d 时,此时 R 为
R = ∫ y = d 1 − x cos θ 1 sin θ 1 f ( x , y ) d s R = \int_{y = \frac{d_1-x \cos\theta_1}{\sin\theta_1}}f(x,y)ds R=∫y=sinθ1d1−xcosθ1f(x,y)ds
将 y y y 替换一下,高等数学中的线积分求解问题。这是一种思路。法二: δ \delta δ 函数
δ \delta δ 函数是一个广义函数。简单形式如下:
δ ( t ) = { 0 , t ≠ 0 1 , t = 0 \delta(t) = \left\{ \begin{aligned} 0, &\quad t\ne 0\\ 1, &\quad t=0 \end{aligned} \right. δ(t)={0,1,t=0t=0
结合上述直线方程 L ( θ , d ) : d − x c o s θ − y s i n θ = 0 L(\theta,d):\ d-xcos\theta-ysin\theta = 0 L(θ,d): d−xcosθ−ysinθ=0, 则有
δ ( d − x c o s θ − y s i n θ ) = { 0 , d − x c o s θ − y s i n θ ≠ 0 1 , d − x c o s θ − y s i n θ = 0 \delta(d-xcos\theta-ysin\theta) = \left\{ \begin{aligned} 0, &\quad d-xcos\theta-ysin\theta\ne 0\\ 1, &\quad d-xcos\theta-ysin\theta=0 \end{aligned} \right. δ(d−xcosθ−ysinθ)={0,1,d−xcosθ−ysinθ=0d−xcosθ−ysinθ=0
最后,radon 变换方程写为:
R ( θ , d ) = ∬ f ( x , y ) ⋅ δ ( d − x c o s θ + y sin θ ) d x d y R(\theta,d) = \iint f(x,y)\cdot \delta(d-xcos\theta+y\sin\theta)dxdy R(θ,d)=∬f(x,y)⋅δ(d−xcosθ+ysinθ)dxdy
当给定 θ , d \theta,d θ,d 时,同样带入计算。
可以总结一下,Radon 变换就是对应 ( θ , d ) (\theta,d) (θ,d) 确定的光线与空间中密度函数的积分。
2.3 Radon 逆变换
想象一下,如果我从不同角度对物体进行照射,得到了每个方向下的投影,即所有 θ , d \theta,d θ,d 对应的 R R R 值。那么反过来,已知 R ( θ , d ) R(\theta,d) R(θ,d) ,是否也就唯一确定 f ( x , y ) f(x,y) f(x,y) 的情况。
至于如何已知 R ( θ , d ) R(\theta,d) R(θ,d) 反求 f ( x , y ) f(x,y) f(x,y) ,现在用不到,挖坑,之后用到再探究其方法。
3. 应用
前面已经提到了一个应用:直线检测(同 Hough 检测一致)
还有个经典应用,即 CT 断层成像的重建。
CT 原理其实就是借助 x 射线照射组织器官,不同组织器官对 x 的射线衰减程度(或系数;对应于上面的 f ( x , y ) f(x,y) f(x,y) )不同,一条 x 射线穿过一系列组织器官后,经衰减后,到达采集设备,得到一个衰减后的强度值(对应于上面的 R R R)。
我们采集得到一系列的 R R R 情况,就可以通过 r a d o n radon radon 逆变换得到衰减信息,即组织器官信息。
换句话说, r a d o n radon radon 变换可用于三维重建,且是三维重建研究方向的helloworld。