MATLAB仿真任意带宽的窄带信号、宽带信号以及全频带信号

一、窄带信号的定义：

如果信号的带宽远小于其中心频率，则该信号成为窄带信号，即

其中，是信号带宽，是信号的中心频率，通常将正弦信号和余弦信号称为正弦型信号，正弦型信号为典型的窄带信号。

窄带信号还有以下定义：

1、B << f 0，即相对带宽B/f 0<< 1 ,一般B/f 0< 0.1。
2、2v/c<<1/TB,其中v 是阵列与目标的相对径向运动速度，c 是信号在介质中的传播速度。
3、( N－1) d/c<<1/B，其中N 是阵元数目，d 是阵元间距。
4、2 Bτθ +1≈1 ,其中τθ是整个阵列以及延迟线的延时之和。
5、该信号空间协方差矩阵在没有噪声时的第二个特征值小于噪声功率。

“1”是对窄带信号的直观理解,在很多文献中均以该定义来区分信号是宽带信号还是窄带信号。
“2”是指在存在相对运动的系统中,在信号的持续时间T 内,相对于信号的距离分辨率,目标没有明显的位移,此时信号可视为窄带信号,否则信号就是宽带信号。
“3”是指在阵列信号处理中,如果信号带宽的倒数远远大于信号掠过阵列孔径的最大传播时间,就称为窄带信号,否则为宽带信号。
“4”和“5”是从阵列采样数据自相关矩阵特征值的角度来定义窄带信号的,窄带情况下,阵列采样数据自相关矩阵的大特征值个数等于信号个数。

可见，窄带信号定义的非一致性决定了宽带信号定义的非绝对性，不同的处理场合使用不同的定义确定信号是否是宽带。

二、宽带信号的定义：

没有文献或组织对宽带信号给出的严格定义，业内一般认为宽带信号与窄带信号是相对的，不满足窄带条件的信号就称为宽带信号。

三、全频带信号的定义：

根据人耳的听力频率范围为20Hz~20000Hz。人耳对于低于20Hz和高于20000Hz的声音无法感知，临床上听力测试的频率范围通常为125-8000Hz。8000-20000Hz为扩展高频，人类的言语频率为500-2000Hz。

因此，全频带信号的频率范围包含了20Hz~20000Hz。

四、matlab仿真任意带宽的窄带信号、宽带信号以及全频带信号

程序如下：

clear 
close all
clc
%%  生成高斯白噪声
fs = 44.1e3;  %采样频率hz
% fs = 15000;  %采样频率hz

T_N=5;         %总时间5s
t=1/fs:1/fs:T_N;  %时间向量
L=T_N*fs;         %样本数量
power=3;          %噪声功率,单位为dbw
z=wgn(1,L,power); %生成高斯白
% z=mapminmax(z,-1,1);

fft_z=fft(z);%快速傅里叶变换之后的噪声
P = abs(fft_z/L);%取幅频特性，除以L
P = P(1:L/2+1);%截取前半段
P(2:end-1)=2*P(2:end-1);%单侧频谱非直流分量记得乘以2
f = fs*(0:(L/2))/L;%频率，最多到一半（奈奎斯特采样定理）

figure
subplot(2,1,1)
plot(t,z)
xlabel("时间/s")
ylabel("幅度/v")
title("高斯白噪声（时域）")
subplot(2,1,2)
plot(f,P)
xlabel("频率/Hz")
ylabel("幅度/v")
title("高斯白噪声（频域）")
%%  滤波200-8000 Hz
[b1,a1]=butter(8,[200/(fs/2),8000/(fs/2) ]);%获得8阶巴特沃斯滤波器系数，得到200-8000 Hz的宽带的时域波形,fs=44100
% figure
% freqs(b,a)%画滤波器特性曲线
lvbo_z1=filter(b1,a1,z);%滤波
file_name1=strcat('mask\200-8000.wav');
audiowrite(file_name1,lvbo_z1,fs);

figure
subplot(2,1,1)
plot(t,lvbo_z1)
xlabel("时间/s")
ylabel("幅度/v")
title("200-8000宽带高斯噪声（时域）")

fft_lvbo_z1=fft(lvbo_z1);%傅里叶变换
lvbo_P1 = abs(fft_lvbo_z1/L);%取幅频特性，除以L
lvbo_P1 = lvbo_P1(1:L/2+1);%截取前半段
lvbo_P1(2:end-1)=2*lvbo_P1(2:end-1);%单侧频谱非直流分量记得乘以2
subplot(2,1,2)
plot(f,lvbo_P1)
xlabel("频率/Hz")
ylabel("幅度/v")
title("200-8000宽带高斯噪声（频域）")

%%  滤波4000-8000 Hz（一倍频程）8000/4000=2
[b2,a2]=butter(9,[4000/(fs/2),8000/(fs/2) ]);%获得8阶巴特沃斯滤波器系数，得到4000-8000 Hz的高通 倍频程的时域波形,fs=44100
% figure
% freqs(b,a)%画滤波器特性曲线
lvbo_z2=filter(b2,a2,z);%滤波
file_name2=strcat('mask\4000-8000.wav');
audiowrite(file_name2,lvbo_z2,fs);

figure
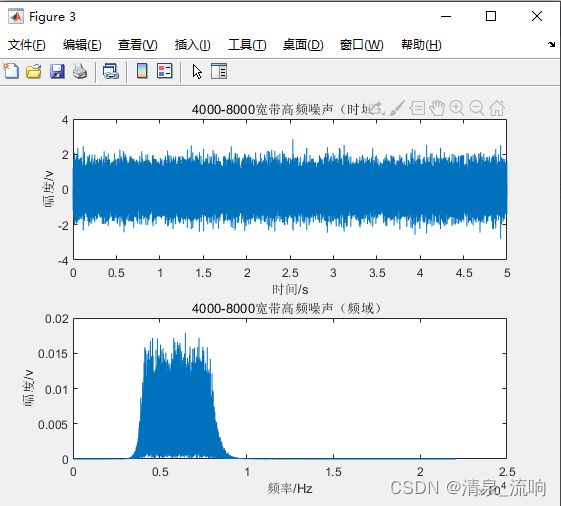
subplot(2,1,1)
plot(t,lvbo_z2)
xlabel("时间/s")
ylabel("幅度/v")
title("4000-8000宽带高频噪声（时域）")

fft_lvbo_z2=fft(lvbo_z2);%傅里叶变换
lvbo_P2 = abs(fft_lvbo_z2/L);%取幅频特性，除以L
lvbo_P2 = lvbo_P2(1:L/2+1);%截取前半段
lvbo_P2(2:end-1)=2*lvbo_P2(2:end-1);%单侧频谱非直流分量记得乘以2
subplot(2,1,2)
plot(f,lvbo_P2)
xlabel("频率/Hz")
ylabel("幅度/v")
title("4000-8000宽带高频噪声（频域）")

%%  滤波2000-8000 Hz（二倍频程）8000/2000=2^2=4
[b3,a3]=butter(9,[2000/(fs/2),8000/(fs/2) ]);%获得8阶巴特沃斯滤波器系数，得到2000-8000 Hz的高通 2倍频程宽带的时域波形,fs=44100
% figure
% freqs(b,a)%画滤波器特性曲线
lvbo_z3=filter(b3,a3,z);%滤波
file_name3=strcat('mask\2000-8000.wav');
audiowrite(file_name3,lvbo_z3,fs);

figure
subplot(2,1,1)
plot(t,lvbo_z3)
xlabel("时间/s")
ylabel("幅度/v")
title("2000-8000宽带高频噪声（时域）")

fft_lvbo_z3=fft(lvbo_z3);%傅里叶变换
lvbo_P3 = abs(fft_lvbo_z3/L);%取幅频特性，除以L
lvbo_P3 = lvbo_P3(1:L/2+1);%截取前半段
lvbo_P3(2:end-1)=2*lvbo_P3(2:end-1);%单侧频谱非直流分量记得乘以2
subplot(2,1,2)
plot(f,lvbo_P3)
xlabel("频率/Hz")
ylabel("幅度/v")
title("2000-8000宽带高频噪声（频域）")


%%  滤波4470-5620 Hz（1/3倍频程）
[b4,a4]=butter(9,[4470/(fs/2),5620/(fs/2) ]);%获得8阶巴特沃斯滤波器系数，得到4470-5620 Hz的高通 1/3倍频程时域波形,fs=44100
% figure
% freqs(b,a)%画滤波器特性曲线
lvbo_z4=filter(b4,a4,z);%滤波
file_name4=strcat('mask\4470-5620.wav');
audiowrite(file_name4,lvbo_z4,fs);

figure
subplot(2,1,1)
plot(t,lvbo_z4)
xlabel("时间/s")
ylabel("幅度/v")
title("4470-5620窄带高频噪声（时域）")

fft_lvbo_z4=fft(lvbo_z4);%傅里叶变换
lvbo_P4 = abs(fft_lvbo_z4/L);%取幅频特性，除以L
lvbo_P4 = lvbo_P4(1:L/2+1);%截取前半段
lvbo_P4(2:end-1)=2*lvbo_P4(2:end-1);%单侧频谱非直流分量记得乘以2
subplot(2,1,2)
plot(f,lvbo_P4)
xlabel("频率/Hz")
ylabel("幅度/v")
title("4470-5620窄带高频噪声（频域）")


%%  滤波447-562 Hz（1/3倍频程）
[b5,a5]=butter(2,[447/(fs/2),562/(fs/2) ]);%获得8阶巴特沃斯滤波器系数，得到447-562 Hz的低通 1/3倍频程时域波形,fs=2000
% figure
% freqs(b,a)%画滤波器特性曲线
lvbo_z5=filter(b5,a5,z);%滤波
file_name5=strcat('mask\447-562.wav');
audiowrite(file_name5,lvbo_z5,fs);

figure
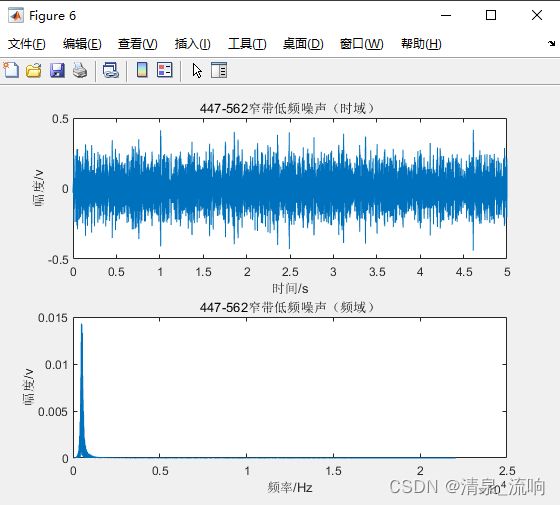
subplot(2,1,1)
plot(t,lvbo_z5)
xlabel("时间/s")
ylabel("幅度/v")
title("447-562窄带低频噪声（时域）")

fft_lvbo_z5=fft(lvbo_z5);%傅里叶变换
lvbo_P5 = abs(fft_lvbo_z5/L);%取幅频特性，除以L
lvbo_P5 = lvbo_P5(1:L/2+1);%截取前半段
lvbo_P5(2:end-1)=2*lvbo_P5(2:end-1);%单侧频谱非直流分量记得乘以2
subplot(2,1,2)
plot(f,lvbo_P5)
xlabel("频率/Hz")
ylabel("幅度/v")
title("447-562窄带低频噪声（频域）")

%%  滤波400-800 Hz（一倍频程）
[b6,a6]=butter(5,[400/(fs/2),800/(fs/2) ]);%获得8阶巴特沃斯滤波器系数，得到400-800 Hz的低通 1/3倍频程时域波形,fs=2000
% figure
% freqs(b,a)%画滤波器特性曲线
lvbo_z6=filter(b6,a6,z);%滤波
file_name6=strcat('mask\400-800.wav');
audiowrite(file_name6,lvbo_z6,fs);

figure
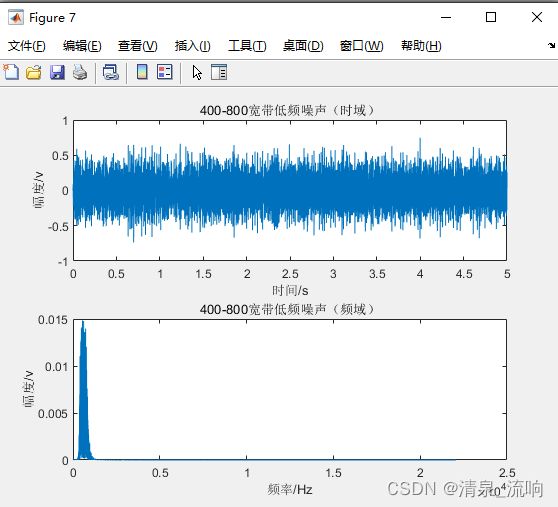
subplot(2,1,1)
plot(t,lvbo_z6)
xlabel("时间/s")
ylabel("幅度/v")
title("400-800宽带低频噪声（时域）")

fft_lvbo_z6=fft(lvbo_z6);%傅里叶变换
lvbo_P6 = abs(fft_lvbo_z6/L);%取幅频特性，除以L
lvbo_P6 = lvbo_P6(1:L/2+1);%截取前半段
lvbo_P6(2:end-1)=2*lvbo_P6(2:end-1);%单侧频谱非直流分量记得乘以2
subplot(2,1,2)
plot(f,lvbo_P6)
xlabel("频率/Hz")
ylabel("幅度/v")
title("400-800宽带低频噪声（频域）")

%%  滤波200-800 Hz（二倍频程）
[b7,a7]=butter(5,[200/(fs/2),800/(fs/2) ]);%获得8阶巴特沃斯滤波器系数，得到200-800 Hz的低通 1/3倍频程时域波形,fs=2000
% figure
% freqs(b,a)%画滤波器特性曲线
lvbo_z7=filter(b7,a7,z);%滤波
file_name7=strcat('mask\200-800.wav');
audiowrite(file_name7,lvbo_z7,fs);

figure
subplot(2,1,1)
plot(t,lvbo_z7)
xlabel("时间/s")
ylabel("幅度/v")
title("200-800宽带低频噪声（时域）")

fft_lvbo_z7=fft(lvbo_z7);%傅里叶变换
lvbo_P7 = abs(fft_lvbo_z7/L);%取幅频特性，除以L
lvbo_P7 = lvbo_P7(1:L/2+1);%截取前半段
lvbo_P7(2:end-1)=2*lvbo_P7(2:end-1);%单侧频谱非直流分量记得乘以2
subplot(2,1,2)
plot(f,lvbo_P7)
xlabel("频率/Hz")
ylabel("幅度/v")
title("200-800宽带低频噪声（频域）")

运行结果如下（部分）：