Isolating Individual Trees in a Savanna Woodland Using Small Footprint Lidar Data

Abstract

这项研究提出了一种从激光雷达数据中检测单个树梢的新方法，并将标记控制的分水岭分割应用于隔离稀树草原林地中的单个树木。通过在具有可变窗口大小的树冠最大值模型(CMM)中搜索局部最大值来检测树梢。与以往方法不同的是，可变窗口大小由树冠大小与树高回归曲线预测区间的下限决定。建立了树冠最大值模型以减少树梢检测的误差。树梢也是基于它们通常位于树冠中心周围的事实来检测的。通过五重交叉验证方法评估树描绘的准确性。结果表明，树木隔离的绝对准确率为64.1%，远高于仅在回归曲线确定的窗口大小内搜索局部最大值的方法的准确率(37.0%)。

Introduction

隔离单个树并从遥感数据中提取相关树结构信息在各种应用中具有重要意义。例如，单个树木级别的详细信息可用于监测森林再生（Gougeon和Leckie，1999；Clark等，2004a和2004b），减少森林清查所需的实地工作（Gong等，1999）和评估森林损害（Leckie等人，1992；Levesque和 King，1999；Kelly 等人，2004）。为了研究植被和气候之间的相互作用，我们在加利福尼亚州Ione的一个涡流协方差塔站点上应用了一个名为MAESTRA的单独的基于树的模型，用于量化碳通量。为了参数化基于单个树木的模型，我们的研究正在进行中，以使用面积为800的小型激光雷达数据提取单个树木结构参数，例如树高、树冠高度、树冠大小、叶面积指数(LAI)和生物量m x 800m围绕涡流协方差塔。然而，为了获得这样的个体树木参数，最初的过程是分离个体树木并描绘树冠边界。

已经对使用遥感数据隔离单个树木进行了深入研究。然而，以往的数据主要集中在大尺度航拍照片或高空间分辨率遥感影像上。从图像或照片中分离出单个树木的方法包括：局部最大值检测（Dralle和Rudemo，1996）、具有固定或可变窗口大小的局部最大值过滤（Wulder等人，2000；Pouliot等人，2002）、山谷追踪（Dralle和Rudemo，1996）。 Gougeon,1995), 使用尺度空间理论进行边缘检测 (Brandtberg and Walter, 1998), 模板匹配(Pollock, 1996; Larsen and Rudemo, 1998), 局部样带分析(Pouliot et al, 2002), 3D建模 (Sheng等人，2001；龚等人，2002）和分水岭分割（Schardt等人，2002；Wang等人，2004）。当从单目图像或照片中分离树木时，这些方法主要基于这样的假设，即在树梢周围存在反射率“峰值”，沿着树冠边缘存在“谷”。然而，“峰”和“谷”并不总是不同的，因为冠层反射率受光照条件、冠层光谱特性和复杂冠层结构等各种因素的影响。

最近，研究人员开始将激光雷达数据应用于个体树木隔离和树冠信息提取（Hyyppä等，2001；Persson等，2002；Brandtberg等，2003；Leckie等，2003；Popescu等，2003；Popescu和韦恩，2004）。与被动成像相比，激光雷达的优势在于直接测量冠层的三维坐标。因此，可以检测几何而不是光谱的“峰”和“谷”。一些研究已经将针对光学图像和航空照片开发的方法扩展到用于树木检测的激光雷达数据（Brandtberg等人，2003年；Leckie等人，2003年）; Popescu等人，2003年）。 Brandtberg等人(2003)将尺度空间理论扩展到检测冠段。 Leckie等人(2003)将山谷跟踪方法应用于激光雷达和多光谱图像，发现激光雷达可以轻松消除大部分出现在露天看台上的错分误差，而光学图像在隔离道格拉斯的树木方面表现更好-冷杉地块。

本研究尝试在树木隔离中使用标记控制的分水岭分割。分水岭分割首先由Beucher和Lantuejoul(1979)提出，是一种广为人知的图像分割方法，它融合了其他分割方法的优点，例如区域增长和边缘检测(Soille, 2003)。为了避免过度分割问题，Meyer和Beucher(1990)引入了标记控制的分水岭分割。这个想法是围绕用户指定的标记而不是输入图像中的局部最大值执行分水岭分割。指示标记位置的图像称为标记函数，生成分水岭的图像称为分割函数。标记控制的流域分割非常适合树隔离。通过适当的标记和分割功能，标记控制的分水岭分割可用于描绘各个树冠的边界。这一特性使其优于局部样带或剖面方法（Pouliot等，2002；Popescu等，2003），后者只能获得有限方向的冠半径。

标记控制的分水岭分割应用于紧凑型机载光谱成像仪 (CASI) 图像中的树木隔离 (Wang et al, 2004)。 Schardt et al (2002) 在激光雷达数据中使用了分离云杉树的阈值，并怀疑它不适合落叶树种，因为它们的树冠结构复杂。在标记控制的分水岭分割中，标记和分割函数的形式在将图像划分为有意义的目标方面起着关键作用。特别是，对应于树梢的标记函数对于其在树隔离中的成功应用至关重要。本研究假设只有在从激光雷达数据中生成适当的标记和分割函数时，才能为落叶树分离出单棵树。基于这些，本研究的目的是提出从激光雷达数据生成树梢标记和分割函数的方法，并测试它们在稀树草原林地树木隔离中的应用。

本文结构如下：首先，讨论了可变窗口大小的树顶检测方法，并介绍了一种创建标记和分割函数的新方法；接下来，评估这些标记和分割功能的性能并分析相关错误；最后，给出结论。

Methods

Study Area and Lidar Data

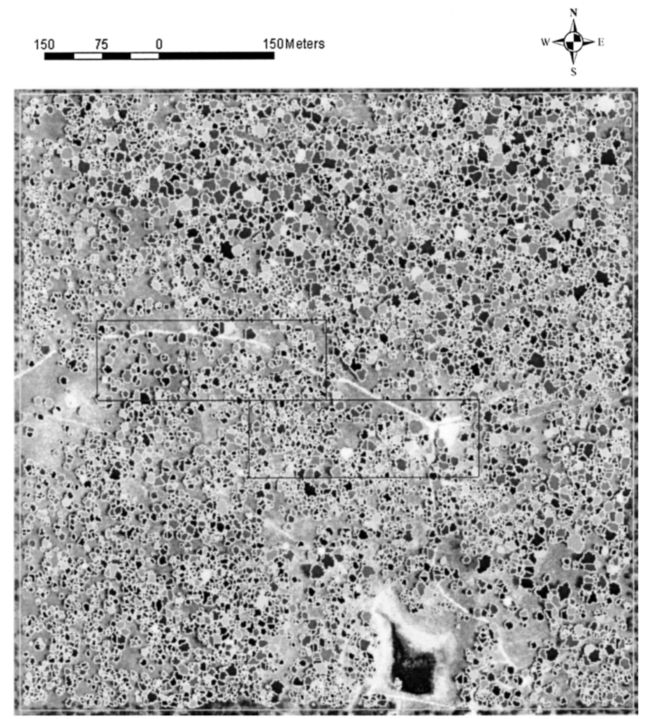
研究地点是一片开阔的橡树稀树草原林地，位于加利福尼亚州的艾奥尼附近(北纬38.26度，西经120.57度)(图1)。该场地位于一个私人牧场上，是美国涡流协方差场场地网络的一部分(Baldocchi等人，2004年)。该景观的特点是地势平坦(最大坡度小于15%)，蓝橡树(Quercus douglasii H.&A .)和少数灰松树散布在连续的地中海一年生草层上。2003年8月24日，Optech ALTM 2025获得了激光测高数据，记录了每个激光脉冲的第一次和最后一次返回。扫描模式为z形。数据提供商声称的垂直精度为18厘米，置信度为95%，水平精度为飞行高度的1/3000。扫描宽度约为300米，飞行高度约为500米，覆盖面积约为18厘米。平均张贴密度为每平方米9.5个点，导致平均斑点间距约为32厘米。为了获得如此高的脉冲密度，该地点飞行了两次。在这项研究中，使用了覆盖涡流协方差塔周围800米×800米的数据来隔离单个树木。

图 1. 覆盖研究区域的CASI图像。

Digital Elevation Model

激光雷达数据中的树木隔离通常基于冠层高度模型(CHM)，它是冠层表面高度与地球表面数字高程模型(DEM)之间的差异。从激光测高数据生成DEM（也称为滤波）的研究仍在进行中。通常，激光脉冲迭代地分为地形和非地形返回，提取的地形脉冲用于通过插值生成DEM（Hyyppä等人，2001；Persson等人，2002；Brandtberg等人，2003）。在本研究中，生成DEM的基本过程如下：

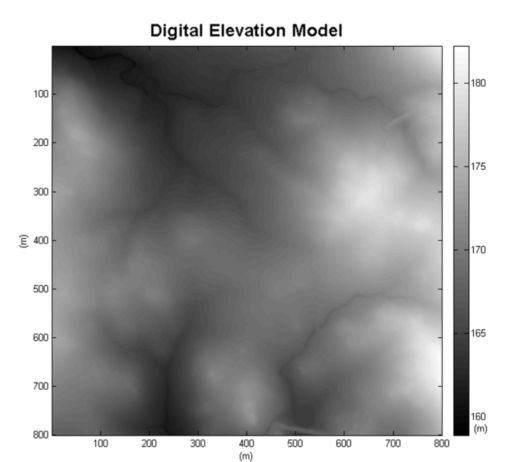
首先，创建一个单元格大小为1m x 1m的网格。每个单元格记录落在单元格中的所有脉冲的最低最后一次返回；这个网格表示为$g_{\min }$。如果某些单元格内没有脉冲，则用最接近的单元格值填充它们；这个填充的网格表示为$g_{\min }$。然后，通过形态学打开填充网格$g_{\min }$创建一个近似地形的表面，表示为$g_{o(f\min )}$。通过计算$g_{\min }$和$g_{f\min }$之间的差异来识别一组初始地形脉冲。将绝对差值小于0.5m的小区视为地形脉冲所在的小区。来自这些单元的三重$\left\{{\mathrm{X}}_{\mathrm{i}},{\mathrm{Y}}_{\mathrm{i}},g_{\min ,i}\right\}$用于通过克里金法创建DEM。通过将每个脉冲的最后一次返回的高程与其DEM值进行比较，获得了一组新的地形脉冲。如果它们的绝对差值小于0.5m，则归类为地形脉冲。该算法的细节在另一篇配套论文中介绍（Chen等人，2007年）。图2显示了DEM。

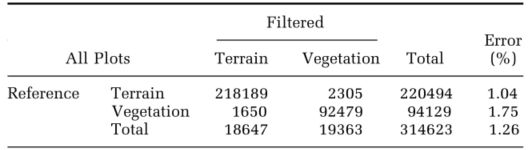
为了评估过滤的准确性，随机定位三个面积为100m x 100m的地块，并将脉冲手动分类为地形和植被返回，这一层作为后续的ground truth。通过计算I型、II型和总误差来评估过滤的准确性（Sithole和Vosselman，2003年）。I类错误是地形返回错误分类为植被返回的百分比。II类错误是被错误分类为地形回波的植被回波的百分比。总误差是用每个参考收益类别的部分加权的误差。精度总结在表1中。过滤的高精度部分是由于研究区域的平坦地形。

图 2. 从激光雷达数据生成的DEM。

表 1. 所有绘图的过滤精度评估表

Canopy Height Mode

创建DEM后，可以计算激光脉冲的相对冠层高度并将其内插到CHM中。以前的研究使用克里金法（Popescu和Wynne，2004年）、主动轮廓算法（Persson等人，2002年）或PCI EASI中的VDEMINT程序（Leckie等人，2003年）来创建CHM或数字表面模型 (DSM)。在Popescu和Wynne(2004)中，首先创建了一个网格，每个网格记录了其中最高的激光脉冲首次返回的高度；然后，通过克里金法将这些单元内的高程内插到CHM中。该方法用于本研究。网格的单元大小是构建CHM的重要参数。较大的像元尺寸将减少冠层高度的变化，并使插值CHM中的“峰”和“谷”难以检测。然而，一个非常小的单元大小可以显着增加数据存储。如果第一回波密度$\lambda$（returns/m²）在研究区域内没有变化，则脉冲之间的平均距离为：
$$d=\sqrt{\frac{1}{\lambda }}(1)$$

单元格大小可以设置为$d$。在实践中，脉冲密度会发生变化，因为条带之间存在侧面重叠，并且此数据集沿条带边缘的脉冲密度较高。因此，当局部脉冲密度较大时，应使用较小的单元尺寸。通过在第一次返回上覆盖1m x 1m单元格的网格来研究$\lambda$的变化。结果显示，$\lambda$每平方米的回报从0到115不等。通过计算$\lambda$的第p个分位数来选择大的$\lambda$。在本研究中，$p$设置为0.99，其对应的$\lambda$值为44。使用等式1，单元大小设置为0.2m。

Variable Window Sizes in Treetops Detection

可以通过在CHM中找到局部最大值（Hyyppä等人，2001；Persson等人，2002）或固定或可变窗口大小内的局部最大值来检测树梢（Dralle和Rudemo，1996；Wulder等人，2000）。使用局部极大值检测树梢时遇到的主要问题是大的错分误差，即非树梢局部极大值被错误地归类为树梢。 Wulder等人(2000)通过在可变窗口大小内搜索局部最大值，从高空间分辨率光学图像中检测到树梢。基于半方差范围或斜率的局部中断自适应地计算窗口大小。Popescu和Wynne(2004)通过假设树高和树冠大小之间的关系推导出可变窗口大小，并使用它们从激光雷达数据中检测树梢。在该数据集中测试了Popescu和Wynne(2004)方法。

为了获得树高和树冠大小之间的关系，从CHM手动测量树高和树冠大小。树高是人工确定的树冠内的最大高度。冠部尺寸是沿两个垂直方向的平均冠部直径。在整个研究区域对树木进行系统采样，水平和垂直间隔为53m。如果采样位置没有树，则选择最近的树。最终样本量为196棵树。

从CHM而不是实地测量树高和树冠大小有几个原因。首先，由于该激光雷达数据集的高脉冲密度，很容易从CHM中手动识别单棵树。第二，在CHM中取样可以大大减少工作量，并且不受现场可及性等因素的限制。为了评估准确性，随机选择另外26棵树，从CHM和现场测量它们的树高和树冠大小。在野外，用高度计测量每棵树的高度八次，然后取平均值。沿两个垂直方向测量树冠尺寸，并使用平均值。CHM和野外测量的树高和树冠大小的平均绝对差分别为0.37m和0.58m。这表明，从CHM中对树木进行采样时，精确度是可以接受的。

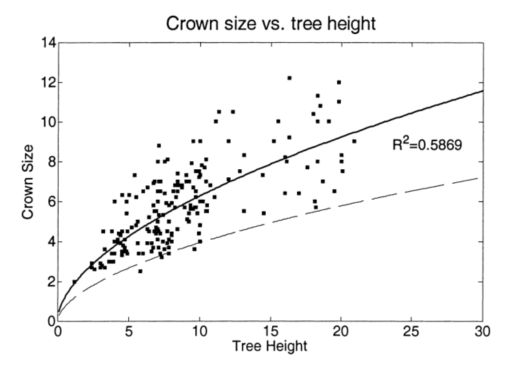
结果发现，当树较高时，树冠大小具有较大的可变性（图 3），如果拟合线性模型，这将违反同方差的假设。为了避免这个问题，适配了一个非线性功率模型:

$$\text{ Crown size }=1.7425\times (\text{ Tree height }{)}^{0.5566}\text{. }(2)$$

Variable Window Size from Prediction Interval

使用等式(2)可以减少错分误差，因为它将在较大的窗口大小内为较高的树搜索局部最大值。但是，这也会导致较大的遗漏误差。据统计，在某一高度有一半的树木的树冠尺寸小于该高度的拟合值(图3)。如果窗口大小等于适合的值，这些树的树梢可能会丢失。在这项研究中，窗口大小由另一条曲线决定，即$1-\alpha$回归模型单侧预测区间的下限(图3)。考虑一个回归模型${\mathrm{Y}}_{\mathrm{x}}={\beta }^{\mathrm{T}}\mathrm{x}+{\epsilon }_{\mathrm{i}}$。曲线由下式确定:

$${\tilde{\mathrm{Y}}}_{\mathrm{x}}=\hat{\mathrm{Y}}-\mathrm{t}(1-\alpha ;\mathrm{n}-2)\sqrt{s^2+xS{x}^{\prime }}(3)$$

其中，${\tilde{\mathrm{Y}}}_x$是给定树高$x$处的预测下限，$s^2$是均方误差，$t$是Student的t累积分布函数的倒数，$S$是系数估计值的协方差矩阵，${\left({\mathrm{X}}^{\mathrm{T}}\mathrm{X}\right)}^{-1}{\mathrm{s}}^2$和$\hat{Y}$是$x$处的拟合值。当$\alpha$为0.5时，下限${\tilde{\mathrm{Y}}}_{\mathrm{x}}$正好位于拟合的回归曲线上。当使用该曲线来确定用于检测树梢的窗口大小时，可以通过使用小的$\alpha$来减少遗漏误差。然而，较小的$\alpha$将导致较大的错分误差(见图4b和4c)。只有当窗口尺寸小于一棵树的树冠尺寸时，才存在将不相关的局部最大值包含为树顶的风险。

图 3. 树冠大小与树高的关系。实线是回归曲线，虚线是预测区间的下限。

Canopy Maxima Model

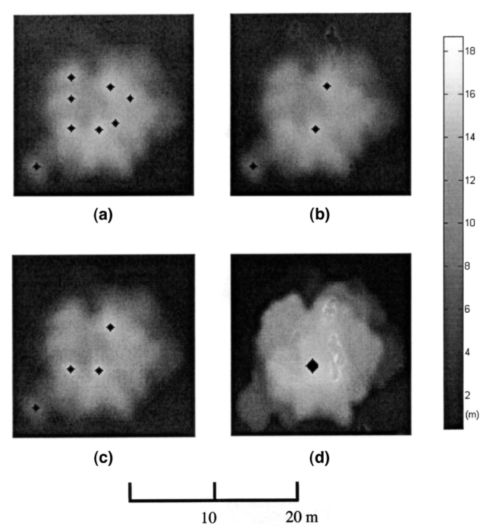
先前的分析表明，在使用冠层高度模型时，不能通过调整$\alpha$同时减少树梢检测的错分和遗漏误差。当从树冠最大值模型(CMM)检测树梢时，可以大大缓解这个问题，CMM是一个规则网格，每个单元格记录其邻域内的最大激光高度。与CHM相比，在CMM中可以去除许多不相关的局部最大值（图4d）。作为检测树顶标记，可变窗口大小用于创建CMM。为了防止树冠之间的“山谷”被填满，窗口尺寸需要小于给定高度下最小树的树冠尺寸。这可以通过在等式3中获得具有非常小的$\alpha$的单边预测区间的下限来进行统计近似。以前的研究人员报告说，在缓坡上的蓝橡树的最大树密度约为20棵树/公顷（Kiang，2002）。对应于这样一个数字，在800m x 800m的研究区域内最多大约有12,800棵树。基于此，$\alpha$设置为0.0001。来自CHM的树高用于通过公式3确定窗口大小。

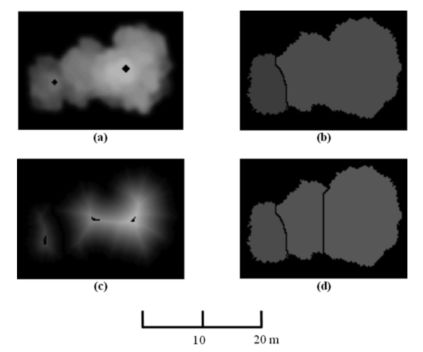
图 4. 使用不同方法和参数检测到的树梢。 (a)通过搜索局部区域最大值从CHM检测到的树梢(b)在$\alpha =0.5$时使用可变窗口大小从CHM检测到的树梢，(c ) 在$\alpha =0.1$时使用可变窗口大小从CHM检测到的树梢，以及(d)检测到的树梢在$\alpha =0.1$时，来自使用可变窗口大小的CMM。

Gaussian Filtering

在CMM中，并非所有非树顶局部最大值都可以被删除，因为用于创建CMM的邻域窗口大小通常小于树冠大小，特别是对于在特定高度具有大树冠的树木。高斯滤波是抑制树梢检测中不相关的局部最大值的典型程序（Dralle 和Rudemo，1996；Hyyppä等，2001；Persson等，2002；Pouliot等，2002；Schardt等，2002；Wang等，2004)。Dralle和Rudemo(1996)发现高斯滤波器的标准差$\sigma$不是很重要。该结论在本研究中得到证实，$\sigma$的值设置为2。但是，滤波器大小对平滑CMM有显着影响。本研究使用的标准是过滤器尺寸不应大于研究区域内最小（就树冠而言）树的树冠尺寸。最小树冠尺寸的确定基于来自CHM的采样树木的树冠尺寸。通过计算在置信水平$(1-\alpha )$下$k$个未来观测值的单边预测区间的下限，可以从样本中近似得出最小的冠尺寸(Hahn and Meeker, 1991)：

$$\text{ Lower Limit }=\bar{X}-t_{1-\frac{\alpha }{k}}(n-1)s\sqrt{1+\frac{1}{n}}\text{, }(4)$$

式中,$\bar{X},s$分别为冠大小样本的均值、标准差和大小（表2）；$\alpha$设置为0.05。根据前面的分析，$k$设置为12,800。

表 2. 采样树的描述性统计数据 (N=196)

当检查样品的树冠尺寸分布时，发现该分布向右倾斜。对正态分布拟合优度的Jarque-Bera检验表明p值为0.0016，这与5%水平的正态分布有显著差异。当转换成对数标度(以e为自然底)时，p值为0.2224。因此，等式4用于获得对数标度下树冠尺寸的单侧预测区间的下限。在转换回原始比例后，获得最小树冠尺寸的值1.0m，其被用作高斯滤波器尺寸。

在平滑的坐标测量机中，除了树梢之外的伪局部最大值大大减少了(见图4c和4d)。在等式4中，主要影响的是遗漏误差，而不是错分误差。应用这样的“分治”策略，可以减少树梢检测的遗漏和错分误差。在检测到树梢后，它们被用于分割单个树冠。

Segmentation with CMM

分水岭分割的过程可以用洪水模拟来说明(Soille，2003)。图5a示出了CMM。为了模拟洪水过程，我们首先计算了CMM的补充量(图5b)，它类似于两个集水池。假设每个盆的最小处都打了一个孔。然后，当它逐渐浸入水中时，集水盆地将被淹没。这种算法可以被认为是沿着分割线自动建造水坝，以防止两个相邻集水池中的水汇合(图5c)。建造的水坝被称为分水线，将被用来分隔树木。

在标记控制的分水岭分割中，在计算其分水岭之前，CMM的补集通过最小值强加被过滤，使得所有非树顶最小值已经被移除。假设有一个图像$f$，在这种情况下它是CMM的补充，并且在每个像素$p$:

$$f_m(p)=\{\begin{array}{ll}0,\text{ if }p\text{ belong to a marker, }& \\ t_{\max }+1,& \text{ otherwise }\end{array}(5)$$
其中${\mathrm{t}}_{\max }$是输入图像$f$的最大值。Minima imposition是先计算$f+1$和标记图像$f_m$之间的像素级最小值，记为$(f+\text{ 1) }\wedge f_m$，然后通过腐蚀进行形态重建来自标记图像$f_m$的$(f+1)\wedge f_m$：
$$f_{mp}=R_{(f+1)\wedge f_m}^r\left(f_m\right),(6)$$

其中$f_{mp}$是施加最小值后的图像，$R_{(f+1)\wedge f_m}^e\left(f_m\right)$定义为$(f+1)\wedge f_m$相对于$f_m$的测地线侵蚀，直到达到稳定为止(Soille, 2003)。 $(f+1)\wedge f_m$的测地线侵蚀相对于$f_m$是对$f_m$进行形态腐蚀，但只有在腐蚀后的值小于$(f+1)\wedge f_m$时才使用$(f+1)\wedge f_m$的值。极小值强制可以重构CMM的补集，使得只有极小值对应于标记的树梢。该图强调了在应用标记控制的分水岭分割方法时，找到正确的树顶标记函数的重要性。

Segmentation with Distance-Transformed Image

落叶树，如橡树，具有相对平坦的树冠表面，使得CMM或CHM难以检测到树梢（图6a）。由于树梢通常位于树冠中心周围，因此可以利用这一事实来进一步检测树梢。为了实现这一点，首先创建了一个二值图像，其中树冠的值为1，而分水岭线和背景的值为0（图6b）。然后，对二值图像进行距离变换，以计算每个非零像素到其最近的零像素的距离（图6c）。在距离变换的图像中，冠的中心具有较大的值。与CMM一样，该距离变换图像的补集，表示为${\mathrm{DIST}}_c$，可用于分割。使用$h$最小值变换从${\mathrm{DIST}}_c$检测到树梢，该变换抑制了所有比$h$-minima的最小值。 ${\mathrm{DIST}}_c$的h-minima变换是通过从${\mathrm{DIST}}_c+h$侵蚀${\mathrm{DIST}}_c$来执行重建。

$$DIS{T}_{c,h\min }=R_{DIS{T}_c}^{\epsilon }\left(DIS{T}_c+h\right)(7)$$
其中$DIS{T}_{c,h\min }$是${\mathrm{DIST}}_c$的$h$最小值变换。将${\mathrm{DIST}}_c$的区域最小值标记为树梢。利用这些树梢标记和分割函数${\mathrm{DIST}}_c$，使用标记控制的分水岭分割来描绘树冠段（图6d）。请注意，阈值$h$直接影响检测树梢的性能。从训练数据中获得了一个最佳的$h$值。

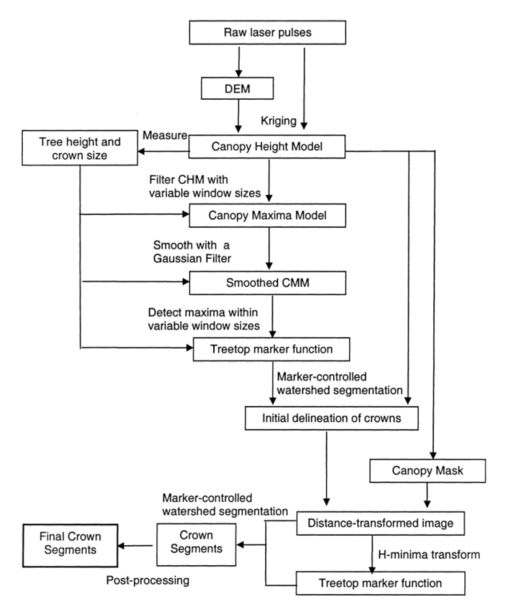
由于场地内有一些枯死的树干和一些生态学研究仪器，因此通过去除所有小于2m的节段对这些节段进行了后处理。与研究地点边界相邻的所有部分也被删除。隔离单个树的整个过程如图7所示。

图 5. 分水岭分割算法示意图。(a)CMM，(b)CMM的补充，和(c )在分界线上建造的水坝。

图 6. 用于树梢检测的距离变换图像。 (a) 在 CMM 中找到的树梢，(b) 在 CMM 中使用树梢的分割结果，(c ) 距离变换的图像和使用 h-minima 变换检测到的树梢，以及 (d) 基于距离变换的图像的分割结果。

图 7. 树隔离方法流程图。

Results and Discussions

Accuracy Assessment

为了评估准确性，通过在现场的CHM打印件上手动描绘树冠边界，获得了两个横断面的ground truth树冠图（图8），每个横断面的面积为100m x 300m。航拍照片被用于实地帮助描绘树冠。在现场勾勒出牙冠边界后，通过在实验室中使用3D可视化软件 (ArcGIS® 3D Analyst, ESRI™) 检查激光点云，进一步验证和完善它们。两个样带共有772棵树。树木隔离的绝对准确度(AATI)用于评估描绘准确度：
$$\mathrm{AATI}=\frac{N_{1,1}}{N_r}(8)$$
其中${\mathrm{N}}_{1,1}$是与ground truth树冠多边形具有一对一关系的树冠数量，${\mathrm{N}}_{\mathrm{r}}$是场地中的树冠数量，${\mathrm{N}}_{\mathrm{s}}$是自动描绘的线段总数。一对一关系意味着ground truth路拱多边形和与之重叠的一个线段之间的重叠面积$S_o$在${\mathrm{S}}_{\mathrm{r}}\pm 10\%\ast {\mathrm{S}}_{\mathrm{r}}$的范围内，其中${\mathrm{S}}_{\mathrm{r}}$是参考路拱多边形的面积。

树隔离方法中有两个自由参数：公式4中的$\alpha$和公式7中的$h$。树隔离精度通过五折交叉验证方法评估，该方法将地面实况数据随机分为五折。每次使用四个折叠进行训练，并使用训练数据达到最高AATI的参数来评估遗漏的折叠的准确性。这个过程重复了五次，平均五次的准确率。调整参数时，$\alpha$和h的域分别被限制为{0.01, 0.1, 0.2, 0.3, 0.4, 0.5}和{0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7}。发现当任意四折用于训练时，当$\alpha$为0.01和$h$为0.5m时获得最高AATI时获得最高AATI。不同折叠的AATI从61.3%到68.2%不等。平均交叉验证准确率为64.1%。使用这些参数值，总共描绘了9,386个段（图8）。

由于不同的研究使用不同的准确性评估方法，因此很难将我们的准确性与其他研究的准确性进行比较。 Persson等人(2002)描绘了瑞典南部的挪威云杉、苏格兰松树和桦树等针叶树的树冠部分。他们通过搜索田野树周围两个像素（三分之二米）内的所有片段，将片段与田野树联系起来。总共有71%的树木被正确检测到。Brandtberg et al (2003)采用模糊概念来量化分割结果的准确性，并设计了一个指数A，如果分割多边形与现场描绘的多边形完美重叠，则其值为1。最后，它们的A值在0.21到0.35之间变化，位于落叶林中的6个一公顷地块，树种包括橡树、枫树和杨树。 Leckie等人(2003)将其视为“完美”匹配，当地面参考多边形和所描绘的线段之间存在一一对应并且它们的重叠大于50%时。他们获得了59%的“完美”匹配针叶林。与这些研究相比，本研究中使用的准确度评估标准要严格得多。因此，使用我们的方法获得的准确性令人鼓舞。

图 8. 冠部轮廓图（$\alpha =0.01$和$h=0.5m$）。两个矩形显示横断面的位置以进行准确性评估。

Effects of α and h

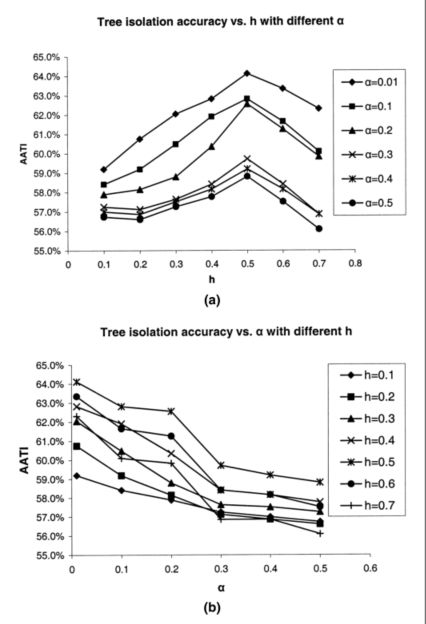
为了检查$\alpha$和$h$的影响，计算了ground truth样带中所有树木的这两个参数的所有组合的AATI（表3）。在研究阈值h对树隔离精度的影响时，有一个一致的模式表明h = 0.5m是该数据集的最佳值（图9a）。当h非常小时，虚假的局部最小值可能被算作树梢，树冠将被过度分割。当h很大时，会丢失树梢，导致分割不足的问题。因此，当h介于这两个极值之间时，可以获得最高的准确度。对于$\alpha$，似乎在降低$\alpha$时树隔离精度会增加。可能的原因之一是在使用平滑CMM检测树梢时，错分错误已大大减少。因此，降低$\alpha$将减少遗漏误差，而对错分错误的影响很小（图9b）。

表 3. 树隔离精度

图 9. 参数对树隔离的影响。

图 10. 不同树顶检测方法的树隔离精度比较。方法1：从CHM中检测树梢，窗口大小基于拟合回归曲线；方法二：通过CMM检测树梢，窗口大小根据回归曲线预测区间的下限；方法3：树梢是CHM内的局部最大值；方法4：除方法3外，从距离变换图像中检测树梢。

Comparison of Different Treetop-detection Methods

除了上述方法之外，其他三种树梢检测方法也应用于标记控制的分水岭分割以进行树隔离：（a）第一种方法是基于 Popescu 和 Wynne（2004），它通过搜索变量内的局部最大值来检测树梢CHM 中的窗口大小。窗口大小由拟合回归曲线确定，（b）在第二种方法中，从CMM中检测树梢，可变窗口大小由回归曲线预测区间的下限确定，但距离变换后的图像是不用于检测树梢，并且（c）在第三种方法中，通过在 CHM 中找到局部最大值来检测树梢。对于所有这三种方法，分割函数都是 CHM。

这三种方法的 AATI 分别为 37.0%、54.4% 和 48.6%（图 10）。基于Popescu和Wynne(2004)的方法的准确度最低。这并不奇怪，因为之前的分析表明，如果窗口大小由拟合回归曲线确定，可能会遗漏大约一半的树。在检测到树梢时，第二种方法的准确度远高于第一种方法从 CMM 和窗口大小由预测区间的下限确定。与第二种方法相比，从距离变换的图像中额外检测树梢的方法可以将准确率提高约10%。第三种方法的准确性也高于Popescu和Wynne(2004)方法。这是因为这种方法的遗漏误差率很低。

Error Analysis

遗漏和错分误差将导致树冠分割不足或过度。当相邻树木的枝条相互缠绕或高度不同的树木紧密生长时，通常很难将它们分开。过度分割问题主要发生在非常古老的橡树上。这些古老而大的橡树通常生长在空旷的地方。由于与周围树木的光照和养分竞争很小，它们的枝条可以向各个方向延伸，并长成不规则的形状。当每个大分支看起来像一棵树时，就会发生过度分割问题。当在 CMM 或距离变换图像中无法辨别树木之间的“山谷”时，树冠边界被错误地描绘。

Conclusion

在这项研究中，重新审视了以前通过在可变窗口大小内搜索局部最大值来检测树梢的方法，发现使用拟合回归曲线确定窗口大小可能会导致较大的遗漏误差。所提出的方法旨在通过三种方式减少遗漏和错分错误：（a）创建CMM以减少虚假的局部最大值，（b）使用基于预测下限的可变窗口大小从CMM检测树梢间隔，以及（c）使用距离变换检测树梢，这是基于树梢位于每个树冠中心周围的事实。第一个手段是减少错分错误，其余两个是减少遗漏误差。研究发现，这种“分而治之”的方法可以达到比传统方法更高的精度。另外，应用距离变换图像检测树梢可以显着提高树的隔离精度。但是，与以前的方法相比，这种方法需要现场数据来训练两个额外的参数$\alpha$和$h$。需要更多的研究来测试这种方法对其他森林类型的影响，并检查$\alpha$和$h$的影响。总体而言，这种方法的准确性令人鼓舞，特别是考虑到准确性评估中使用的严格标准。结果表明，标记控制的流域分割可用于分离落叶树种的个体树木。树木分离结果可进一步用于提取其他森林参数，如树高、树冠大小、生物量和LAI。利用从遥感数据中提取的单棵树信息，可以对生物地球化学模型进行参数化，以从单棵树扩展到景观，以便更好地了解各种生态过程。

References

Baldocchi, D.D., L. Xu, and N. Kiang, 2004. How plant functionaltype, weather, seasonal drought, and soil physical properties alter water and energy fluxes of an oak-grass savanna and an annual grassland, Agricultural and Forest Meteorology, 123:13–39.

Beucher, S., and C. Lantuejoul, 1979. Use of watersheds in contour detection, International Workshop on Image Processing, Realtime Edge and Motion Detection/Estimation, Rennes, France.

Brandtberg, T., and F. Walter, 1998. Automated delineation of individual tree crowns in high spatial resolution aerial images by multiple-scale analysis, Machine Vision and Applications, 11:64–73.

Brandtberg, T., T.A. Warner, R.E. Landenberger, and J.B. McGraw, 2003. Detection and analysis of individual leaf-off tree crowns in small footprint, high sampling density lidar data from eastern deciduous forest in North America, Remote Sensing of Environment, 85:290–303.

Chen, Q., P. Gong, and D.D. Baldocchi., 2007. Filtering airborne laser scanning data with morphological methods, Photogrammetric Engineering & Remote Sensing, In press.

Clark, D.B., C.S. Castro, L.D.A. Alvarado, and J.M. Read, 2004a.Quantifying mortality of tropical rain forest trees using highspatial-resolution satellite data, Ecological Letters, 7:52–59.

Clark, D.B., J.M. Read, M.L. Clark, A.M. Cruz, M.F. Dotti, and D.A. Clark, 2004b. Application of 1-m and 4-m resolution satellite data to ecological studies of tropical rain forests, Ecological Applications, 14:61–74.

Dralle, K., and M. Rudemo, 1996. Stem number estimation by kernel smoothing of aerial photos, Canadian Journal of Forest Research, 26:1228–1236.

Gong, P., G.S. Biging, S.M. Lee, X. Mei, Y. Sheng, R. Pu, B. Xu, K. Schwarz, and M. Mostafa, 1999. Photo ecometrics for forest inventory, Geographic Information Science, 5:9–14.

Gong, P., Y. Sheng, and G.S. Biging, 2002. 3D Model-based Tree measurement from high-resolution aerial imagery, Photogrammetric Engineering & Remote Sensing, 68:203–1212.

Gougeon, F.A., 1995. A crown-following approach to the automatic delineation of individual tree crowns in high spatial resolution aerial images, Canadian Journal of Remote Sensing, 21:274–284.

Gougeon, F.A., and D.G. Leckie, 1999. Forest regeneration: Individual tree crown detection techniques for density and stocking assessment, Proceedings of the International Forum on Automated Interpretation of High Spatial Resolution Digital Imagery for Forestry, 10–12 February 1998, Victoria, B.C., Pacific Forestry Center, Canadian Forest Service, Natural Resources Canada, pp. 11–23.

Hahn, G.H., and W.Q. Meeker, 1991. Statistical Intervals: A Guide for Practitioners, John Wiley & Sons, Inc., New York.

Hyyppä, J., O. Kelle, M. Lehikoinen, and M. Inkinen, 2001. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners, IEEE Transactions on Geoscience and Remote Sensing, 39:969–975.

Kelly, M., D. Shaari, Q.H. Guo, and D.S. Liu, 2004. A comparison of standard and hybrid classifier methods for mapping hardwood mortality in areas affected by “sudden oak death,” Photogrammetric Engineering & Remote Sensing, 70:1229–1239.

Kiang, N.Y., 2002. Savannas and Seasonal Drought: The Landscapeleaf Connection Through Optimal Stomatal Control, Ph.D.

dissertation, Department of Environmental Science, Policy, and Management, University of California at Berkeley, Berkeley, California, 303 p.

Larsen, M., and M. Rudemo, 1998. Optimizing templates for finding trees in aerial photographs, Pattern Recognition Letters, 19(12): 1153–1162.

Leckie, D.G., X. Yuan, D.P. Ostaff, H. Piene, and D.A. Maclean, 1992. Analysis of high spatial resolution multispectral MEIS imagery for spruce budworm damage assessment on a single tree basis, Remote Sensing of Environment, 40:125–136.

Leckie D., F. Gougeon, D. Hill, R. Quinn, L. Armstrong, and R. Shreenan, 2003. Combined high-density lidar and multispectral imagery for individual tree crown analysis, Canadian Journal of Remote Sensing, 29(5):1–17.

Levesque, J., and D.J. King, 1999. Airborne digital camera image semivariance for evaluation of forest structural damage at an acid mine site, Remote Sensing of Environment, 68:112–124.

Meyer, F., and S. Beucher, 1990. Morphological segmentation, Journal of Visual Communication and Image Representation, 1:21–46.

Persson, Å., J. Holmgren, and U. Söderman, 2002. Detecting and measuring individual trees using an airborne laser scanner, Photogrammetric Engineering & Remote Sensing, 68:925–932.

Pollock, R., 1996. The Automatic Recognition of Individual Trees in Aerial Images of Forests Based on a Synthetic Tree Crown Model, Ph.D. dissertation, Department of Computer Science, University of British Columbia, Vancouver, B.C.

Popescu, S.C., R.H. Wynne, and R.F. Nelson, 2003. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass, Canadian Journal of Remote Sensing, 29:564–577.

Popescu, S.C., and R.H. Wynne, 2004. Seeing the trees in the forest: Using lidar and multispectral data fusion with local filtering and variable window size for estimating tree height, Photogrammetric Engineering & Remote Sensing, 70:589–604.

Pouliot, D.A., D.J. King, F.W. Bell, and D.G. Pitt, 2002. Automated tree crown detection and delineation in high-resolution digital camera imagery of coniferous forest regeneration, Remote Sensing of Environment, 82:322–334.