GNSS算法进阶(三)- 利用doppler更新kalman滤波中的速度状态量+动态测试效果
rtklib中的速度
在rtklib中,RTK算法中的PVA模型,没有使用doppler观测值对速度进行更新。rtklib中的动态模型中的速度实际是位置历元差分的结果,加速度是速度差分结果。在状态更新时,预测状态由状态转移矩阵乘以上一个历元的状态得到,那么预测状态的协方差阵中就会存在位置/速度/加速度之间的相关关系。
在使用观测值对位置进行更新时,由于各个状态量之间的相关性,速度和加速度也会相应的变化。但实质上,仅有位置状态量的更新信息,所以速度和加速度的精度会比较低,并不能比较好的利用载体的运动状态模型。
doppler观测值相对于伪距,最明显的特点是,基本不受电离层和对流层的影响。另外,卫星的轨道和钟差的速度项的精度也相对较高。所以理论上,使用doppler进行载体速度测量的精度,一般可以达到厘米到分米量级。
利用doppler进行更新
为了令单点定位的状态预测精度更高,所以我准备在单点定位中增加doppler观测值的使用。
考虑到现在的kalman滤波单点定位的状态量已经确定了,即位置/速度/加速度/各系统接收机钟,状态量中并未考虑接收机钟漂。
同时考虑到在将来RTK算法中,没有接收机钟相关的状态量,所以本次我们对doppler观测值取星间单差,消去接收机钟漂误差,更加符合我们现在的kalman单点定位流程,在将来扩展RTK算法时,也会比较容易的复用。
在原有的LSQ单点定位流程中,RTKLIB中存在基于doppler使用最小二乘计算接收机速度的相关代码。本次只需要将其稍作修改,增加对多频的适配。同时后续的代码,我都会增加上注释说明,方便初学者更容易理解。doppler残差计算函数如下:
/* range rate residuals of mul-freq
*
* Input:
* @obs: observations
* @n: number of observations
* @rs: satelltes' postion and velocity
* @dts: satellites' clock and clock drift
* @nav: ephemeris
* @rr: receiver approximate positon
* @x: velocity state in filter
* @azel: azimuth and elevation of satellites
* @vsat: satellites is visiable?
*
* Output:
* @v: doppler residuals
* @var: variance
* @H: design matrix
*
*/
static int resdop_mulfreq_filter(const obsd_t *obs, const int n, const double *rs, const double *dts,
const nav_t *nav, const double *rr, const prcopt_t *opt, const double *x,
const double *azel, const int *vsat, double *v, double *var, double *H)
{
double freq, rate, pos[3], E[9], a[3], e[3], vs[3], cosel, sig, e_ref[3] = {0.0}, v_ref = 0.0;
int i, j, nv = 0, sys, freq_idx;
trace(3, "resdop : n=%d\n", n);
ecef2pos(rr, pos);
xyz2enu(pos, E);
for (i = 0; i < n && i < MAXOBS; i++)
{
if (!(sys = satsys(obs[i].sat, NULL)) || !vsat[i] || norm(rs + 3 + i * 6, 3) <= 0.0)
{
continue;
}
/* LOS (line-of-sight) vector in ECEF */
cosel = cos(azel[1 + i * 2]);
a[0] = sin(azel[i * 2]) * cosel;
a[1] = cos(azel[i * 2]) * cosel;
a[2] = sin(azel[1 + i * 2]);
matmul("TN", 3, 1, 3, 1.0, E, a, 0.0, e);
/* satellite velocity relative to receiver in ECEF */
for (j = 0; j < 3; j++)
{
vs[j] = rs[j + 3 + i * 6] - x[j];
}
/* range rate with earth rotation correction */
rate = dot(vs, e, 3) + OMGE / CLIGHT * (rs[4 + i * 6] * rr[0] + rs[1 + i * 6] * x[0] - rs[3 + i * 6] * rr[1] - rs[i * 6] * x[1]);
for (freq_idx = 0; freq_idx < opt->nf; freq_idx++)
{
freq = sat2freq(obs[i].sat, obs[i].code[freq_idx], nav);
if (obs[i].D[freq_idx] == 0.0 || freq == 0.0)
{
continue;
}
/* range rate residual (m/s). */
v[nv] = (-obs[i].D[freq_idx] * CLIGHT / freq - (rate - CLIGHT * dts[1 + i * 2])) - v_ref;
/* variance of pseudorange error */
var[nv] = varerr(opt, azel[1 + i * 2], sys);
/* design matrix */
for (j = 0; j < 3; j++)
{
H[j + 3 + nv * NX_F] = -e[j] - e_ref[j];
}
if (v_ref == 0.0)
{
v_ref = v[nv];
for (j = 0; j < 3; j++)
{
e_ref[j] = -e[j];
}
continue;
}
if (fabs(H[3 + nv * NX_F]) < 1e-8)
{
continue;
}
nv++;
}
}
return nv;
}另外,在调用此函数的逻辑也比较简单,注意与伪距残差的兼容。具体详细请看代码的提交记录。
nv += resdop_mulfreq_filter(obs, n, rs, dts, nav, x, &rtk->opt, x + 3, azel, vsat, v + nv, var + nv, H + nv * NX_F);代码请在公众号后台回复 git 获取,然后记得切换到 mulfreq-spp分支。
本次修改提交的commit:
4e0fb34e8b0d5e91ba638fddcc899f7d9e191b58
结果分析
同时还提交了一组动态数据,动态数据来自
(https://github.com/IPNL-POLYU/UrbanNavDataset)
我也将其fork到了国内的gitee上
(https://gitee.com/wutong2008/UrbanNavDataset2 )
同时为了对比自己的结果,与提供的基准结果的误差。使用python写了简单的对比工具,也随上一个commit提交到了代码库中。有时间会简单介绍一下如何使用,逻辑很简单,也可以自行去使用。
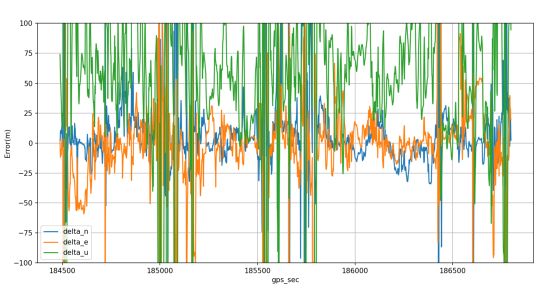
原始RTKLIB单点定位结果,即使用第一个频点伪距观测值,电离层和对流层均使用模型改正,使用最小二乘进行数据处理。
结果存在较多的历元丢失。
进一步排查发现,丢失原因是大量的历元在valpos函数中无法通过残差的卡方检验,禁用valpos函数后的结果如下,有明显提升。因为是城市动态结果,并且使用的ublox消费级模组,结果差在预期之内。
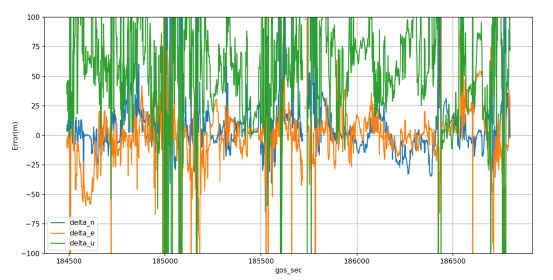
使用我写的kalman滤波的结果,使用第一个频点伪距观测值,电离层和对流层均使用模型改正,使用kalman滤波进行数据处理。从该结果来看,kalman滤波较最小二乘没有明显提升,则是因为我们预测的状态量精度太低。
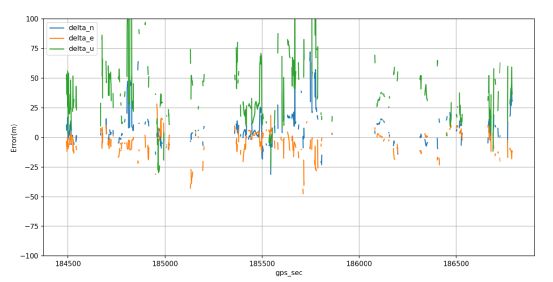
kalman滤波结果,配置未变,增加doppler观测值,对速度进行更新。结果较未增加doppler之前,“毛刺点”明显减少,定位精度也有一定提升。
但定位精度依然较差,因为观测值中存在粗差,即有些观测量的方差信息我们给的不合适。需要进一步优化。
公众号
有时会将代码 或者资源放在个人公众号上,有问题,在公众号后台回复,也回答的比较快一些,欢迎关注 GNSS和自动驾驶
其他相关文章链接汇总
GNSS算法学习系列教程 - 文章列表_梧桐Fighting的博客-CSDN博客