c++求矩阵的秩_【教学笔记】线性代数 | 第四章 相似矩阵与二次型 要点掌握

【相似矩阵要点总结】

其实整个相似矩阵的重点就在以下四张图里，算法涉及到三阶带参行列式的求解、初等行变换求解方程组、和施密特正交化，只是这一章我们新学了很多概念和知识点，需要在不同的情境下去使用这个算法。

1. 特征值与特征向量的定义、计算及重要定理

这部分的要点主要是为了引出后面相似变换中要用到的一些定理，我们在课堂上讲了四五个定理，但是最重要的就是上图中显示的那两条。

第一，互不相同的特征值对应的特征向量线性无关。无论其对应的是基础解系向量只有一个的特征向量，还是基础解系有多个的特征向量，并在一起都是线性无关的。

第二，n阶方阵最多只有n个线性无关的特征向量。这是由于特征值的代数重数总是大于或等于其几何重数，所以不可能会出现大于方阵阶数的无关的特征向量个数。注意，这里的个数是指基础解系中基向量的个数哦。

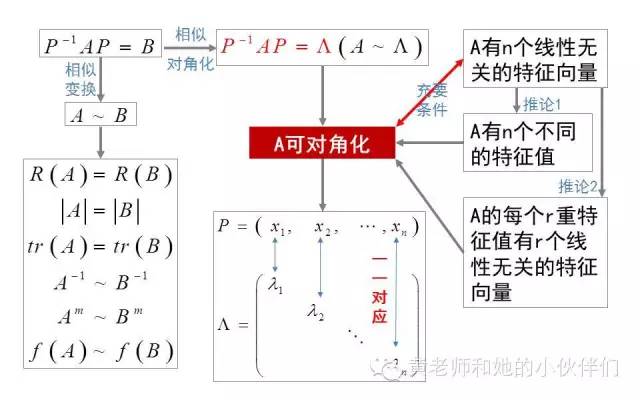
2. 相似变换与对角化的定义、性质与重要定理

我们说过，因为相似矩阵具有相同的特征值、行列式、秩等特点，而如果某方阵刚好能与极其简单的对角矩阵相似，那么我们就可以通过研究简单的对角矩阵来分析原方阵的性质，这使得我们的工程计算大大简化。

而这部分主要解答两个问题：

1. 什么样的方阵才可以对角化？

2. 怎样求得方阵对角化后的对角矩阵及变换矩阵？

对于第一个问题，我们通过定理证明知道，

只有具有n个线性无关的特征向量的方阵才能对角化。

而上节课告诉我们，不同的特征值对应的特征向量线性无关，

因此，具有n个互不相同特征值的方阵也可以对角化。

而事实往往不尽如人意，对吧，我们总是会出现重特征值的情况。

而重特征值有时求出的几何重数小于其代数重数，就不能对角化了。

此时，只有r重特征值具有r个线性无关的特征向量的方阵才能对角化(这样我们n阶方阵A才能得到n个线性无关的特征向量啊)。

对于第二个问题呢，其实通过定理的证明，我们知道，

所谓的相似变换后得到的对角矩阵呢，就是特征值为对角元素的对角阵嘛；而相似变换矩阵就是与特征值一一对应的特征向量组成的方阵嘛。

所以，相似变换的内容我们用上图就可以概括了。

3. 实对称对角化的性质与计算步骤

而后面的二次型矩阵就是对称矩阵，因此实对称矩阵对角化的内容，其实就对二次型正交变换化标准形的内容进行了铺垫。

【二次型矩阵要点总结】

二次型的重点就是掌握两个知识点：

1 ) 化二次型为标准形；

2)判断二次型的正定性。

第一，化标准形的方法教材上介绍的有三种，其中的初等变换法不要求掌握，而配方法其实属于中学的知识内容，利用代数公式配成完全平方式的方法，只是加上了线性变换的概念，最重要的方法则是正交变换法。

1. 正交变换法(从A出发)

【正交变换】Q是n阶正交矩阵，x=Qy即为正交变换。

正交变换可保持向量的内积、范数与夹角不变，因此在几何空间中，正交变换保持几何图形的大小和形状不变。

【定理】对于任意的n元实二次型，总有正交矩阵Q，可以经x=Qy将二次型化为标准型。而标准形中所有平方项的系数为二次型矩阵A的特征值，其所对应的正交单位特征向量则构成了变换矩阵Q.

因此，我们可得到正交变换法化标准形的步骤：

1)写出二次型矩阵A(唯一一步与实对称矩阵对角化不同的地方);

2) 求A的所有特征值与特征向量；

3)若有重特征值，将其对应的特征向量正交化；

4)将所有的特征向量单位化，得到Q。

2. 配方法(从f出发)

由于可逆线性变换不改变二次型的正定性，因此我们就可以将二次型化为标准形后，更好地判断二次型的正定性啦。也就引出了我们最后一节课程内容，学习各种判断二次型正定性的方法。

第二，就是熟练掌握几个判定正定二次型的常用定理。总结如下：

注：上图中的定理序号是刘三阳、马建荣老师编写的教材里的序号。

那么，往年笔试卷中的证明题总是倾向于有关正定矩阵的题型！！！因此，要尤其关注上图中的7种判断方式。而其中的第7条通常只用于带有实际数据的题型。其他几条应根据题中已知条件，找出最靠近的判断方式去证明，较为常用的有1，4，6。

##FINALLY! 线性代数课程内容回顾就到此结束啦！##

~~前面课程精讲视频：

第一章 矩阵及其应用：

【教学笔记】线性代数精讲视频 | 1.1 高斯消元法

【教学笔记】线性代数精讲视频 | 1.2 矩阵的概念及运算

【教学笔记】线性代数精讲视频 | 1.3 可逆矩阵

【教学笔记】线性代数精讲视频 | 1.4 分块矩阵

【教学笔记】线性代数精讲视频 | 1.5 初等变换与初等矩阵

【教学笔记】线性代数精讲视频 | 1.6 矩阵的秩与线性方程组

【教学笔记】线性代数习题册精讲视频 | 第一章 矩阵及应用 计算与证明题

【教学笔记】线性代数习题册精讲视频 | 第一章矩阵及应用 填空与选择题

第二章 行列式：

【教学笔记】线性代数精讲视频 | 2.1 行列式的概念与性质

【教学笔记】线性代数精讲视频 | 2.1 行列式逆序数与排列版定义补充

【教学笔记】线性代数精讲视频 | 2.2 行列式的计算

【教学笔记】线性代数精讲视频 | 2.3 行列式的应用

【教学笔记】线性代数补充知识点 | K阶子式

【教学笔记】线性代数习题精讲 | 第二章 行列式 选择和填空题

【教学笔记】线性代数习题精讲 | 第二章 行列式 计算与证明题

【教学笔记】线性代数习题精讲 | 矩阵的秩与线性方程组的解

第三章 n维向量与向量空间：

【教学笔记】线性代数精讲视频 | 3.1 n维向量

【教学笔记】线性代数精讲视频 | 3.2 向量组的线性相关性

【教学笔记】线性代数精讲视频 | 3.3 向量组的秩与极大无关组

【教学笔记】线性代数精讲视频 | 3.4 n维向量空间

【教学笔记】线性代数精讲视频 | 3.5 基、坐标与维数

【教学笔记】线性代数精讲视频 | 3.6 线性方程组解的结构

【教学笔记】线性代数习题精讲 | 第四章向量空间-计算题与证明题1-21

【教学笔记】线性代数习题精讲 | 第四章向量空间-计算题与证明题22-38

【教学笔记】线性代数习题精讲 | 第四章向量空间-填空题与选择题