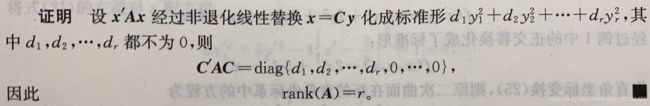高等代数 二次型与矩阵的合同(第6章)1 二次型,标准形,规范形

一.二次型(6.1)
1.概念:

2.非退化线性替换:

准确地说,应该是将$x$用$Cx$带入(这样能保证代换前后二次型中的元不变),但习惯上都记为将$x$用$Cy$带入

3.二次型的等价与矩阵的合同
(1)概念:

(2)判定:

命题1:数域$K$上的2个$n$元二次型$x^{\prime }Ax,y^{\prime }By$等价当且仅当$n$级对称矩阵$A,B$合同

如果将数域$K$改为任意的域$F$,结论仍成立

(3)合同类:

二.二次型的标准型(6.1)
1.概念:

注意:①1个二次型的标准形可以不唯一

2.实数域上的标准型:

命题2:实数域上的$n$元二次型$x^{\prime }Ax$有1个标准型为$${\lambda }_1{y}_1^2+{\lambda }_2{y}_2^2+...+{\lambda }_n{y}_n^2(10)$$其中${\lambda }_1,{\lambda }_2...{\lambda }_n$是$A$的全部特征值

3.正交替换:

4.任意数域上的标准型
(1)利用配方法求解:



(2)利用矩阵的合同证明:

引理1:设$A,B$都是数域$K$上的$n$级矩阵,则$A\simeq B$,当且仅当$A$经过一系列初等行/列变换可以变成$B$.此时对$I$作上述初等行/列变换中的初等列变换,就得到1个可逆矩阵$C$,使得$C^{\prime }AC=B$

定理1:数域$K$上任一$n$级对称矩阵都合同于1个对角矩阵

定理2:数域$K$上任一$n$元二次型都等价于1个只含平方项的二次型

注:①以上2个定理中的数域$K$都可被扩展为特征不为2的域$F$

(3)利用成对的初等行/列变换求解:

4.二次型的秩:

命题3:数域$K$上$n$元二次型$x^{\prime }Ax$的任一标准形中,系数不为0的平方项的个数等于该二次型的矩阵$A$的秩

二次型$x^{\prime }Ax$的矩阵$A$的秩就称为二次型$x^{\prime }Ax$的秩

三.实二次型的规范形(6.2)
1.实二次型的规范形
(1)概念:

(2)唯一性:

定理3(惯性定理):$n$元实二次型$x^{\prime }Ax$的规范形是唯一的

2.惯性指数与符号差
(1)概念:

(2)实二次型等价的判定:

命题4:2个$n$元实二次型等价
$\iff$它们的规范形相同
$\iff$它们的秩相等,并且正惯性指数也相等

(3)平方项个数于惯性指数的关系:

(4)矩阵的惯性指数与合同规范形:

(定理3的)推论1:任一$n$级实对称矩阵$A\simeq diag\{1...1,-1...-1,0...0\}$,其中1的个数等于$x^{\prime }Ax$的正惯性指数,-1的个数等于$x^{\prime }Ax$的负惯性指数(分别把它们称为$A$的正/负惯性指数),该对角矩阵称为$A$的合同规范形

(命题4的)推论1:2个$n$级实对称矩阵合同
$\iff$它们的秩相等,并且正惯性指数也相等

四.复二次型的规范形(6.2)
1.概念:
2.唯一性:

定理4:复二次型$x^{\prime }Ax$的规范形是唯一的

3.复二次型等价的判定:

命题5:2个$n$元复二次型等价
$\iff$它们的规范形相同
$\iff$它们的秩相等
推论1:任一$n$级复对称矩阵$A$合同于对角阵$$\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]$$其中$r=rank(A)$
推论2:2个$n$级复对称矩阵合同
$\iff$它们的秩相等
由推论2立得:秩是$n$级复对称矩阵组成的集合在合同关系下的完全不变量