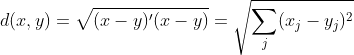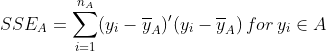多元统计分析——聚类分析——层次聚类
| 聚类方法 | 适用场景 | 代表算法 | 优点 | 缺陷 | 延伸 |
| 层次聚类 | 小样本数据 | - | 可以形成类相似度层次图谱,便于直观的确定类之间的划分。 该方法可以得到较理想的分类 |
难以处理大量样本,计算复杂度高 | |
| 基于划分的聚类 | 大样本数据 | K-means算法 |
|
|
|
| 两步法聚类 | 大样本数据 | BIRCH算法 | 层次法和k-means法的结合,具有运算速度快、不需要大量递归运算、节省存储空间的优点 | - | |
| 基于密度的聚类 |
大样本数据 | DBSCAN算法 |
|
当簇的密度变化太大时,会有麻烦对于高维问题,密度定义是个比较麻烦的问题 | |
| 密度最大值算法 | - | - |
一、聚类分析的直观理解
在科学研究、社会调查、甚至是日常生活中,我们有时需要通过观察个体的特征,将群体中的个体归为不同的族群/簇(Cluster):
- 在市场营销中,基于历史交易信息、消费者背景等对顾客进行划分,从而对不同类型的消费者实施不同的营销策略——精准营销。
- 在金融领域,为获得较为平衡的投资组合,需要首先基于一系列金融表现变量(如回报率、波动率、市场资本等)对投资产品(如股票)进行归类。
- 同样的归类思想也可以应用于天文学、考古学、医学、化学、教育学、心理学、语言学和社会学等。
以上的归类过程均称为聚类分析(Cluster analysis)
二、聚类 vs 分类
在分类分析中,个体的类别标签固有存在,只是对于新观测个体暂时未知,分类过程旨在根据其特征预测预测类别,后续可知是否预测准确,故属于有监督学习(supervised learning)。
在聚类分析中,类别的个数及个体标签本身并不存在,只是根据个体特征的相似性形成“合理”的聚集,并无“正确答案”参考,故其属于无监督学习(unsupervised learning)。
聚类常用于数据探索或者挖掘前期,在没有做先验经验的背景下做的探索性分析,也适用于样本量较大情况下的数据预处理工作。
聚类分析无法提供明确的行动指向,聚类结果更多是为后期挖掘和分析工作提供处理和参考,无法回答“为什么”和“怎么办”的问题,更无法为客户提供明确的解决问题的规则和条件(例如决策树条件或关联规则),因此,聚类分析无法真正解决问题。
三、聚类分析概述
合理的聚类方式应使得同一族群内的观测尽可能地“相似”,但不同族群之间有明显区分。那么,如何刻画“相似度”?如下图,从直观的视觉上看,“距离”越小越相似。由此,我们可以将下边的点聚成3类。
1、相似度的度量——距离
回顾两个![]() 维观测个体
维观测个体![]() 和
和![]() ,它们之间的距离可以由以下几种常用方式度量:
,它们之间的距离可以由以下几种常用方式度量:
1.1、欧式距离(Euclidean distance)/L2
一般采取的距离都是欧式距离。
1.2、马氏距离(Mahalanobis distance)
![]()
注意:聚类问题,在聚类成的不同类别当中,协方差矩阵![]() 很难是相同的,所以消除量纲影响的马氏距离反而在大多数情况下是不合理的,因为很难找到一个公共的协方差矩阵
很难是相同的,所以消除量纲影响的马氏距离反而在大多数情况下是不合理的,因为很难找到一个公共的协方差矩阵![]() 。
。
1.3、Minkowski测度( Minkowski metric)
1.4、Canberra测度(Canberra metric)
2、距离矩阵(欧式距离)计算逻辑
对于![]() 个样本观测
个样本观测![]() ,可计算距离矩阵(Distance/Proximity matrix),
,可计算距离矩阵(Distance/Proximity matrix), ![]() ,这里
,这里![]() ,距离矩阵所呈现的是
,距离矩阵所呈现的是![]() 个样本两两之间的距离。
个样本两两之间的距离。
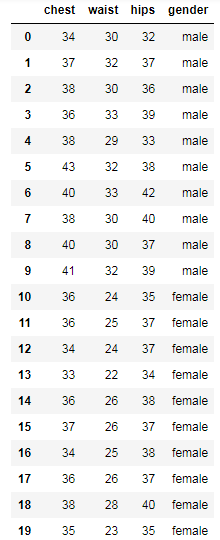
例:20位志愿者的三围数据:
import pandas as pd
import numpy as np
data = pd.read_excel("D:/CDA/dataset/data_cluster1.xlsx")
data输出:
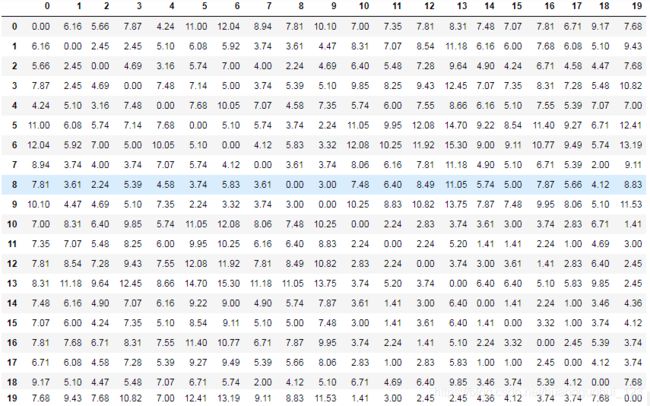
2.1、计算距离矩阵
import scipy.cluster.hierarchy as sch #层次聚类
A=data.iloc[:,:3]
# A是一个向量矩阵:euclidean代表欧式距离
distA=sch.distance.pdist(A,metric='euclidean')
# squareform:将distA数组变成一个矩阵
distB = pd.DataFrame(sch.distance.squareform(distA.round(2)),columns=[i for i in range(20)],index=[i for i in range(20)])
distB输出:
以上即为距离矩阵,呈现的是一个类似“对称矩阵”。
四、层次聚类
1、概述
定义了距离之后,怎样找到“合理”的规则,使相似的/距离小的个体聚成一个族群?
考虑所有的群组组合(先罗列所有可能的群组组合,从中挑出最优的)显然在计算上很难实现,所以一种常用的聚类方法为层次聚类/系统聚类(hierarchical clustering) 。
1.1、层次聚类的方向
层次聚类有两个方向:
-
凝聚法(Agglomerative clustering):由单个个体开始(把单个个体当成不同的群体),逐步将最“相似”的个体连结起来,直到所有个体都合并为一个族群。
-
分离层次法(Divisive clustering):凝聚法的相反方向。
以下文章我们主要讨论凝聚法,分离层次法暂不讨论。
1.2、系统树图
层次聚类过程的结果可以利用图表展示为系统树图(Dendrogram)。系统树图显示了层次聚类的每一个步骤及其结果,包括合并族群带来的距离的变化(包括可以得知两两族群在哪个高度被合并在一起等)。
上图右下的系统树图,主要用于基因的分析当中,即不仅考虑样本的聚类,也考虑变量的聚类。如基因分析当中,横轴可表示为不同的人的聚类,纵轴可表示为他们的基因的信息,即考虑两个维度的聚类情况。
2、层次聚类的类型
从系统树图中可以看出,凝聚法每一步需要合并“距离最小的两个族群”,不同族群间距离的定义方法决定了不同的聚类结果。
2.1、连接方法(Linkage method)
2.1.1、简单连接法(Single linkage)
简单连接(Single linkage)/最近邻方法(Nearest neighbor method) 定义族群间的距离为两族群中相隔最近的两个体间的距离![]() ,这里
,这里![]() 是某一种距离的度量,例如欧式距离。
是某一种距离的度量,例如欧式距离。
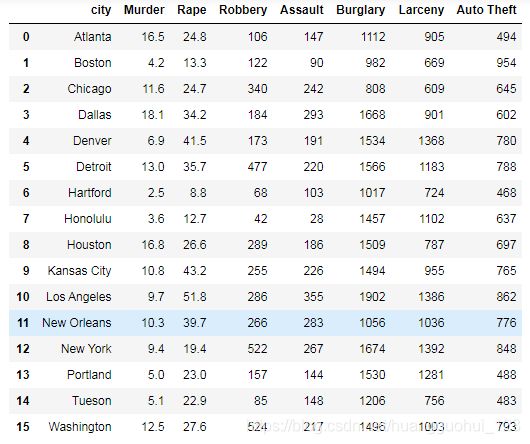
案例:下表展示的数据为美国各城市每10万人的犯罪数量
import pandas as pd
import numpy as np
data = pd.read_excel("D:/CDA/dataset/data_cluster2.xlsx")
data输出:
2.1.1.1、计算距离矩阵
为了更加方便地说明,我们这里先关注前6个城市,其距离矩阵![]() 如下:
如下:
import scipy.cluster.hierarchy as sch #层次聚类
A=data.iloc[:6,1:]
# A是一个向量矩阵:euclidean代表欧式距离
distA=sch.distance.pdist(A,metric='euclidean')
# squareform:将distA数组变成一个矩阵
distB = pd.DataFrame(sch.distance.squareform(distA.round(2)),columns=list(data.iloc[:6,0]),index=list(data.iloc[:6,0]))
distB输出:
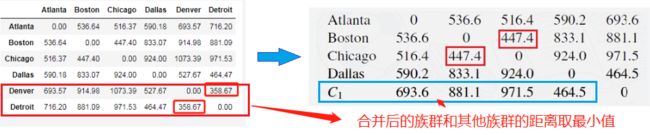
最小的距离是Denver与Detroit之间的358.7,因此这两个城市首先被组合为一个族群![]() 。
。
下一步需计算Atlanta、Boston、Chicago、Dallas和![]() 之间的距离矩阵:
之间的距离矩阵:
最小的距离是 Boston 和 Chicago 之间的447.4,故将两者合并为一个族群![]() 。
。
进一步计算 Atlant、Dallas、![]() 和
和![]() 之间的距离矩阵:
之间的距离矩阵:
最小的距离是Dallas和![]() 之间的464.5,故将其二者合并为
之间的464.5,故将其二者合并为![]() 。
。
Atlanta、![]() 和
和![]() 的距离矩阵为
的距离矩阵为
最小的距离是516.4,据此将其合并为![]() 。此时
。此时![]() 和
和![]() 的距离为:590.2。
的距离为:590.2。
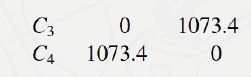
将两者合并得到最后一个族群:![]() 。
。
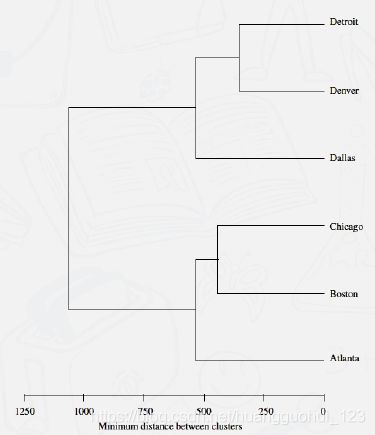
以上前6个城市结果的系统树图展示:
由上图我们可以看出在哪个距离,我们合并了哪个族群, 例如Denver和Detroit我们从图中大致能看到在距离将近400的时候合并成一个族群。
2.1.1.2、 绘制层次聚类图
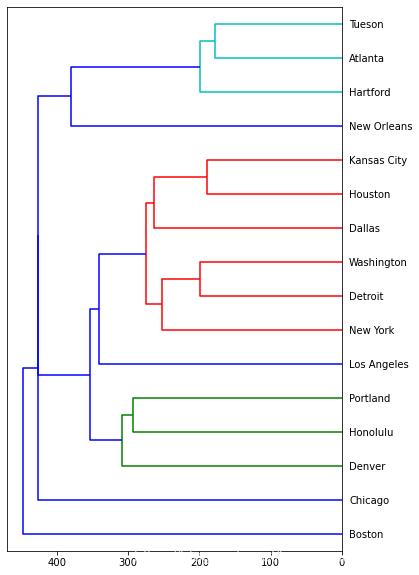
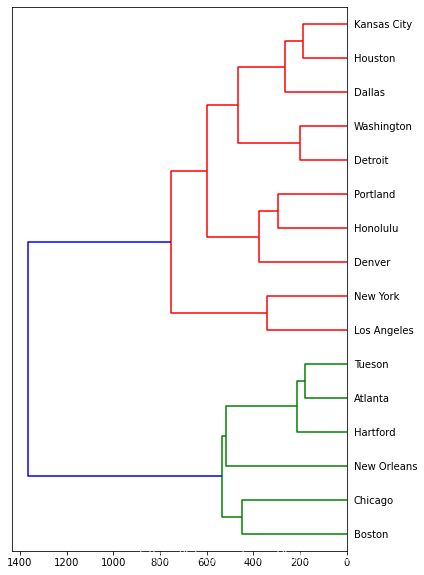
对全部16个城市进行简单连接层次聚类分析:
import scipy.cluster.hierarchy as sch #层次聚类
import matplotlib.pyplot as plt
A=data.iloc[:,1:]
Z = sch.linkage(A, method ='single',metric='euclidean') #euclidean代表欧式距离,#single代表简单连接
#将层次聚类结果以树状图表示出来
fig=plt.figure(figsize=(6,10)) #表示绘制图形的画板尺寸为6*4.5;
sch.dendrogram(Z,labels = data['city'].values
,orientation='left' #横向或者纵向呈现
,leaf_rotation=0 #标签文字是否旋转
,leaf_font_size=10 #标签文字大小
) 输出:
2.1.1.3、 裁剪
#不同的位置裁剪即可得到不同的聚类数目
label = sch.cut_tree(Z,height=400)
data['cut_level_400']=label
data输出:
高度取的是400(可见层次分类图),根据层次聚类图明显是聚成四类。
2.1.1.4、 绘制两个主成分方向坐标的散点图
为了将聚类结果可视化,我们需要降维,因为在大多数情况下,我们处理数据的维度超过2维,因此可以使用主成分分析法,找到占据方差最大的两个维度的散点得到,然后进行绘图,来观察结果。
from sklearn.decomposition import PCA
pca = PCA(n_components = 0.95) #选择方差累积占比95%的主成分
A=data.iloc[:,1:8]
pca.fit(A) #主城分析时每一行是一个输入数据
result = pca.transform(A) #计算结果
fig=plt.figure(figsize=(10,6)) #表示绘制图形的画板尺寸为6*4.5;
plt.scatter(result[:, 0], result[:, 1], c=data['cut_level_400'], edgecolor='k') #绘制两个主成分组成坐标的散点图
for i in range(result[:,0].size):
plt.text(result[i,0],result[i,1],data['city'].values[i]) #在每个点边上绘制数据名称
x_label = 'PC1(%s%%)' % round((pca.explained_variance_ratio_[0]*100.0),2) #x轴标签字符串
y_label = 'PC1(%s%%)' % round((pca.explained_variance_ratio_[1]*100.0),2) #y轴标签字符串
plt.xlabel(x_label) #绘制x轴标签
plt.ylabel(y_label) #绘制y轴标签输出:
根据该图,我们可以看到大致分为四类比较合理,因此上一小节层次聚类裁剪的高度取了一个可以裁剪得到四类的高度400。
2.1.1.5、 绘制热图
#绘制热图
import seaborn as sns
A=data.iloc[:,1:8]
sns.clustermap(A,method ='single',metric='euclidean')输出:
注意:图中方块的颜色深浅仅仅代表原始数值的大小。
2.1.2、完全连接法(Complete linkage)
完全连接(Complete linkage)/最远邻方法(Farthest neighbormethod)中,以两组别中最远个体之间的距离来定义族群之间的距离:![]() 。
。
回到之前城市犯罪率的例子,我们对前6个城市进行完全连接层次聚类:
最小的距离是Denver与Detroit之间的358.7,因此这两个城市首先被组合为一个族群![]() 。
。
注意:因为第一步是根据初始距离矩阵划分,故无论用哪一种层次聚类结果是一样的。
下一步需计算Atlanta、Boston、Chicago、Dallas和![]() 之间的距离矩阵:
之间的距离矩阵:
注意这个距离矩阵中![]() (上面右图中的蓝色框框)与其他城市的距离与简单连接方法不同。
(上面右图中的蓝色框框)与其他城市的距离与简单连接方法不同。
最小的距离是 Boston 和 Chicago 之间的447.4,故将两者合并为一个族群![]() 。
。
进一步计算 Atlant、Dallas、![]() 和
和![]() 之间的距离矩阵:
之间的距离矩阵:
最小的距离是Dallas和![]() 之间的527.7,故将其二者合并为
之间的527.7,故将其二者合并为![]() 。
。
Atlanta、![]() 和
和![]() 的距离矩阵为
的距离矩阵为
最小的距离是536.6,据此将其合并为![]() 。此时
。此时![]() 和
和![]() 的距离为:590.2。
的距离为:590.2。
将两者合并得到最后一个族群:![]() 。
。
以上前6个城市结果的系统树图展示:
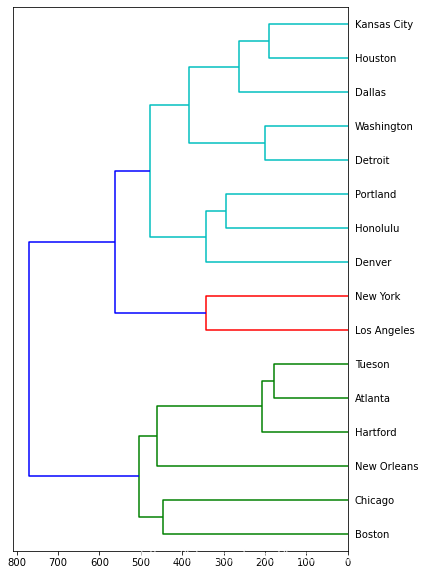
对全部16个城市进行完全连接层次聚类分析,绘制层次聚类图:
import scipy.cluster.hierarchy as sch #层次聚类
import matplotlib.pyplot as plt
A=data.iloc[:,1:]
Z = sch.linkage(A, method ='complete',metric='euclidean') #euclidean代表欧式距离,#complete代表完全连接
#将层次聚类结果以树状图表示出来
fig=plt.figure(figsize=(6,10)) #表示绘制图形的画板尺寸为6*4.5;
sch.dendrogram(Z,labels = data['city'].values
,orientation='left' #横向或者纵向呈现
,leaf_rotation=0 #标签文字是否旋转
,leaf_font_size=10 #标签文字大小
) 输出:
从上图我们看出,完全连接对比简单连接,在合并族群的距离上有所不同。
2.1.3、平均连接法(Average linkage)
平均连接法(Average linkage)中,两族群之间的距离定义为![]() 个
个![]() 集合点和
集合点和![]() 个
个![]() 集合点产生的所有
集合点产生的所有![]() 个距离数值的平均:
个距离数值的平均:![]() 。
。
“距离”计算逻辑的比较——平均连接与简单连接、完全连接
![]()
对全部16个城市进行平均连接层次聚类分析,绘制层次聚类图:
import scipy.cluster.hierarchy as sch #层次聚类
import matplotlib.pyplot as plt
A=data.iloc[:,1:]
Z = sch.linkage(A, method ='average',metric='euclidean') #euclidean代表欧式距离,#average代表平均连接
#将层次聚类结果以树状图表示出来
fig=plt.figure(figsize=(6,10)) #表示绘制图形的画板尺寸为6*4.5;
sch.dendrogram(Z,labels = data['city'].values
,orientation='left' #横向或者纵向呈现
,leaf_rotation=0 #标签文字是否旋转
,leaf_font_size=10 #标签文字大小
) 输出:
对于犯罪率数据,平均连接的聚类结果与完全连接相同,但族群间的距离不同。
2.1.4、质心法(Centroid method)
质心法(Centroid method)中,两族群的距离定义为两族群各自的质心(Centroid),即样本均值向量,之间的欧式距离:![]() ,其中
,其中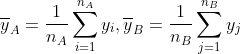 ,在族群合并后,新族群的质心由所有族群内样本点求平均得到:
,在族群合并后,新族群的质心由所有族群内样本点求平均得到:![]() 。
。
对全部16个城市进行质心连接层次聚类分析,绘制层次聚类图:
import scipy.cluster.hierarchy as sch #层次聚类
import matplotlib.pyplot as plt
A=data.iloc[:,1:]
Z = sch.linkage(A, method ='centroid',metric='euclidean') #euclidean代表欧式距离,#centroid代表质心连接
#将层次聚类结果以树状图表示出来
fig=plt.figure(figsize=(6,10)) #表示绘制图形的画板尺寸为6*4.5;
sch.dendrogram(Z,labels = data['city'].values
,orientation='left' #横向或者纵向呈现
,leaf_rotation=0 #标签文字是否旋转
,leaf_font_size=10 #标签文字大小
) 输出:
如果两个族群合并之后,下一步合并时的最小距离反而减小(质心在不断变化),我们则称这种情况为倒置(Reversal/Inversion),在系统树图中表现为交叉(Crossover)现象。
在一些层次聚类方法中,如简单连接、完全连接和平均连接,倒置不可能发生,这些距离的度量是单调的(monotonic)。显然质心方法并不是单调的。
2.1.5、基于中点的质心法
在质心法中,族群合并后,新族群的质心为![]() 。类似加权平均的计算逻辑,如果族群
。类似加权平均的计算逻辑,如果族群![]() 和
和![]() 的样本量差很多,例如
的样本量差很多,例如![]() 包含更多观测,则新质心
包含更多观测,则新质心![]() 可能会由
可能会由![]() 主导,而使
主导,而使![]() 的贡献被忽略。
的贡献被忽略。
为了避免这种情况,我们可以用两族群质心连线的中点作为合并后新组别的质心:![]() 。
。
对全部16个城市进行基于中点的质心连接层次聚类分析,绘制层次聚类图。
import scipy.cluster.hierarchy as sch #层次聚类
import matplotlib.pyplot as plt
A=data.iloc[:,1:]
Z = sch.linkage(A, method ='median',metric='euclidean') #euclidean代表欧式距离,#median代表基于中点质心连接
#将层次聚类结果以树状图表示出来
fig=plt.figure(figsize=(6,10)) #表示绘制图形的画板尺寸为6*4.5;
sch.dendrogram(Z,labels = data['city'].values
,orientation='left' #横向或者纵向呈现
,leaf_rotation=0 #标签文字是否旋转
,leaf_font_size=10 #标签文字大小
) 输出:
基于中点的质心法的系统树图与质心法的结果非常类似。主要源自总样本量较小,样本集合间的样本量差别不大,故质心变化不大。
2.2、Ward方法
Ward法(Ward’s method)/方差平方和增量法(Incremental sum of squares) 由合并前后的族群内方差平方和的差异![]() 定义距离。记
定义距离。记![]() 为族群
为族群![]() 和
和![]() 合并而得的族群,则合并前后的族群内方差平方和分别为:
合并而得的族群,则合并前后的族群内方差平方和分别为:
由Ward法合并的两个族群![]() 和
和![]() ,应使得
,应使得![]() 在合并前后的增量
在合并前后的增量![]() 最小。
最小。
如果质心方法中的距离取平方,Ward法和质方法的唯一区别在于系数![]() :Ward法倾向于合并样本量较小的族群。
:Ward法倾向于合并样本量较小的族群。
对全部16个城市进行基于ward法层次聚类分析,绘制层次聚类图。
import scipy.cluster.hierarchy as sch #层次聚类
import matplotlib.pyplot as plt
A=data.iloc[:,1:]
Z = sch.linkage(A, method ='ward',metric='euclidean') #euclidean代表欧式距离,#ward代表ward法
#将层次聚类结果以树状图表示出来
fig=plt.figure(figsize=(6,10)) #表示绘制图形的画板尺寸为6*4.5;
sch.dendrogram(Z,labels = data['city'].values
,orientation='left' #横向或者纵向呈现
,leaf_rotation=0 #标签文字是否旋转
,leaf_font_size=10 #标签文字大小
) 输出:
由层次聚类图可以看出,ward聚类法倾向于尽量先将个体两两合并成一个群体,之后在合并的基础之上再尽量两两合并,且在距离上,越往上聚类,距离几乎呈指数增长。
3、族群个数的选择
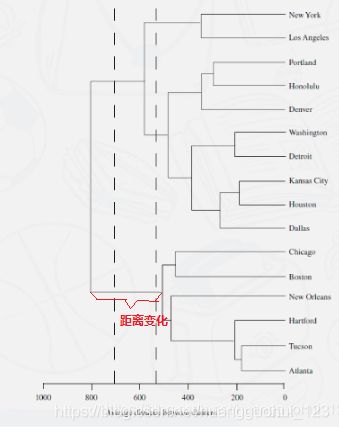
如上图,从不同的距离点位切开,我们可以得到不同个数的族群, 有时族群个数可根据经验或合理的业务解释预先设定。
如果由数据驱动,在层次聚类中,可以从系统树图中于给定距离水平下“切分”树图得到![]() 个族群。我们希望确定
个族群。我们希望确定![]() 的值来最好地拟合数据,一种方法是寻找合并组别时较大的距离变化的节点,如果距离变化较小,说明合并之后的族群和合并之前的族群差别不是很大。
的值来最好地拟合数据,一种方法是寻找合并组别时较大的距离变化的节点,如果距离变化较小,说明合并之后的族群和合并之前的族群差别不是很大。
4、层次聚类算法总结
-
建立
 个初始族群,每个族群中只有一个个体。
个初始族群,每个族群中只有一个个体。 -
计算
 个族群间的距离矩阵。
个族群间的距离矩阵。 -
合并距离最小的两个族群(如果是ward法,则是合并方差平方和增量
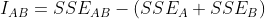 最小的两个族群)。
最小的两个族群)。 -
计算新族群间的距离矩阵(不同连接法,合并后的族群与其他族群的距离计算逻辑不同)。如果组别数为1,则无法再合并,转步骤5;否则转步骤3。
-
绘制系统树图。
-
选择族群个数
 。
。
5、层次聚类python实例
例:回到20位志愿者的三围数据:chest胸围、waist腰围、hips臀围,探讨用这三围的数据,聚类的结果能否反映性别(gender)的差异?
import pandas as pd
import numpy as np
data = pd.read_excel("D:/CDA/dataset/data_cluster1.xlsx")
data输出:
2.1、计算距离矩阵
from scipy.spatial.distance import pdist
from scipy.spatial.distance import squareform
A=data.iloc[:,:3]
# A是一个向量矩阵:euclidean代表欧式距离
distA=pdist(A,metric='euclidean')
# 将distA数组变成一个矩阵
distB = pd.DataFrame(squareform(distA.round(2)),columns=[i+1 for i in range(20)],index=[i+1 for i in range(20)])
distB输出:
2.2、利用简单连接、完全连接、平均连接、质心法、基于中点的质心法和ward法进行层次聚类,并绘制层次聚类图
import scipy.cluster.hierarchy as sch #层次聚类
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
A=data.iloc[:,:3]
fig=plt.figure(figsize=(13.5,16)) #表示绘制图形的画板尺寸为6*4.5;
method_type=['single','complete','average','centroid','median','ward'] #定义层次聚类方法集
hlines_cut=[3.8,10,8,7,8,15] #定义分类高度集
for i in range(len(method_type)):
ax=fig.add_subplot(2,3,i+1)
Z = sch.linkage(A, method =method_type[i],metric='euclidean') #euclidean代表欧式距离。
#绘制层次聚类图
sch.dendrogram(Z,labels = data.index.values,leaf_rotation=0 ,leaf_font_size=10)
plt.hlines(y=hlines_cut[i],xmin=0,xmax=1000,linestyles='dashed')
plt.annotate('分类高度',xy=(0,hlines_cut[i]),xytext=(30,hlines_cut[i]+0.3) ,color='r',arrowprops=dict(arrowstyle="->",color='red',connectionstyle="arc3"))
plt.title(method_type[i])
输出:
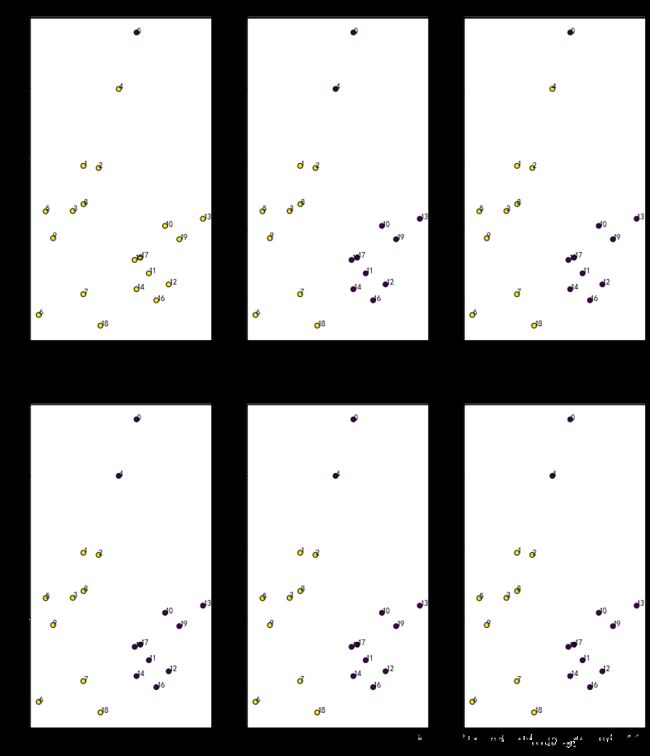
2.3、分成两类,画出带聚类族群标签的主成分散点图
import scipy.cluster.hierarchy as sch #层次聚类
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
plt.rcParams['font.sans-serif']=['SimHei'] #用来显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
A=data.iloc[:,:3]
#提取两个主成分
pca = PCA(n_components = 0.95) #选择方差累积占比95%的主成分
result =pca.fit_transform(A) #主成分分析
fig=plt.figure(figsize=(13.5,16)) #表示绘制图形的画板尺寸
method_type=['single','complete','average','centroid','median','ward'] #定义层次聚类方法集
for i in range(len(method_type)):
ax=fig.add_subplot(2,3,i+1)
Z = sch.linkage(A, method =method_type[i],metric='euclidean') #euclidean代表欧式距离。
#裁剪分类
label = sch.cut_tree(Z,n_clusters=2) #n_clusters直接切成几类,主要用于质心法等会出现交叉现象的层次树
data['cluster_%s'%(method_type[i])]=label
#绘制散点图
plt.scatter(result[:, 0], result[:, 1], c=data['cluster_%s'%(method_type[i])], edgecolor='k') #绘制两个主成分组成坐标的散点图
for j in range(result[:,0].size):
plt.text(result[j,0],result[j,1],data.index.values[j]) #在每个点边上绘制数据名称
x_label = 'PC1(%s%%)' % round((pca.explained_variance_ratio_[0]*100.0),2) #x轴标签字符串
y_label = 'PC2(%s%%)' % round((pca.explained_variance_ratio_[1]*100.0),2) #y轴标签字符串
plt.xlabel(x_label) #绘制x轴标签
plt.ylabel(y_label) #绘制y轴标签
plt.title(method_type[i])输出:
简单连接法存在“链式”(Chaining)问题,倾向于将新的个体归入已存在的族群,而不是创建新的族群。完全连接法正好相反,倾向于将新的两两个体先合并(创建新的族群)。
完全连接聚类和平均连接聚类的结果相似,男士(除去0和4号个体)和女士(除去18号个体)大致各自聚为一个族群。