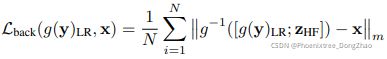可逆去噪网络（CVPR2021）：Invertible Denoising Network: A Light Solution for Real Noise Removal
[paper] [github]
Abstract
Invertible networks have various benefits for image denoising since they are lightweight, information-lossless, and memory-saving during back-propagation. However, applying invertible models to remove noise is challenging because the input is noisy, and the reversed output is clean, following two different distributions.
We propose an invertible denoising network, InvDN, to address this challenge. InvDN transforms the noisy input into a low-resolution clean image and a latent representation containing noise. To discard noise and restore the clean image, InvDN replaces the noisy latent representation with another one sampled from a prior distribution during reversion.
The denoising performance of InvDN is better than all the existing competitive models, achieving a new state-of-the-art result for the SIDD dataset while enjoying less run time. Moreover, the size of InvDN is far smaller, only having 4.2% of the number of parameters compared to the most recently proposed DANet. Further, via manipulating the noisy latent representation, InvDN is also able to generate noise more similar to the original one.
首先，提出动机：优点（轻量级，无丢失信息，节约内存）和挑战（输入和输出遵循两种不同的分布）并存！
其次，核心思想：InvDN 将噪声输入转换为低分辨率的干净图像和包含噪声的潜在表示。为了去除噪声并恢复干净的图像，InvDN 将带有噪声的潜在表示替换为在还原过程中从先验分布中采样的另一个表示。
最后，性能总结：去噪效果好；轻量级；能保存噪声的潜在表示。
Introduction
Image denoising aims to restore clean images from noisy observations. Traditional approaches model denoising as a maximum a posteriori (MAP) optimization problem, with assumptions on the distribution of noise [38, 57, 12], and natural image priors [16, 39, 47]. Although these algorithms achieve satisfactory performance on removing synthetic noise, their effectiveness on real-world noise is compromised since their assumptions deviate from those in real-world scenarios. Recently, convolutional neural networks (CNNs) have achieved superior denoising performance [53, 54]. These CNNs learn the features of images from a large number of clean and noisy image pairs. However, since real noise is very complex, to achieve better denoising accuracy, CNN denoising models have become increasingly large and complicated [50, 51, 52]. Thus, although some methods can achieve very impressive denoising results, they may not be practical in realistic scenarios such as deploying the model on edge equipment like smartphones and motion sensing devices.
分析已有算法的不足。当然，这些不足正是本文能够解决的问题。
Currently, a substantial amount of research has been devoted to developing neural networks that are invertible [18, 41, 25, 9]. For image denoising, invertible networks are advantageous from the following three aspects: (1) the model is light, as encoding and decoding use the same parameters; (2) they preserve details of the input data since invertible networks are information-lossless [36]; (3) they save memory during back-propagation because they use a constant amount of memory to compute gradients, regardless of the depth of the network [23]. Hence, invertible models are suitable for small devices like smartphones. We thus study employing invertible networks to address the problem of image denoising. However, applying such networks to remove noise is non-trivial. The original inputs and the reversed results of the traditional invertible models follow the same distribution [19, 31, 46]. In contrast, for image denoising, the input is noisy, and the restored image is clean, following two different distributions. Therefore, invertible denoising networks are required to abandon the noise in the latent space before the reversion. Due to this difficulty, noise removal has not previously been studied and deployed in invertible literature and models.
In this paper, we propose an invertible denoising network, InvDN, to resolve the above difficulties. Unlike previous invertible models, two different latent variables are involved; one incorporates noise and high-frequency clean contents while the other only encodes the clean part. During the forward pass, InvDN transforms the input image to a downscaled latent representation with an increased number of channels. We train InvDN to make the first three channels of the latent representation the same as the low-resolution clean image. Since invertible networks preserve all the information of the input [36], noisy signals are in the rest of the channels. To remove noise completely, we discard all the channels that contain noise. However, as a sideeffect, we also lose some information corresponding to the high-resolution clean image. To reconstruct such missing information, we sample a new latent variable from a prior distribution and combine it with the low-resolution image to restore the clean image.
首句，用 difficulties, Unlike 等词汇，凸显本文的贡献。
然后介绍 forward pass，然后很自然的描述到去噪过程产生的问题，即去掉噪声表示通道的过程，不可避免的去掉了一些影响高分辨率图像的信息。最后，提出解决方法，即从先验分布中抽样一个新的潜在变量，并将其合并到低分辨率图像中，去重构高分辨率图像。
Invertible Denoising Network
Invertible Neural Network
Invertible networks are originally designed for unsupervised learning of probabilistic models [19]. These networks can transform a distribution to another distribution through a bijective function without losing information [36]. Thus, it can learn the exact density of observations. Using invertible networks, images following a complex distribution can be generated through mapping a given latent variable
, which follows a simple distribution
, to an image instance
, i.e.,
, where
is the bijective function learned by the network. Due to the bijective mapping and exact density estimation properties, invertible networks have received increasing attention in recent years and have been applied successfully in applications such as image generation [19, 31] and rescaling [46].
介绍了可逆神经网络的特点（可以通过一个双目标函数将一个分布转换为另一个分布而不会丢失信息）、功能、应用（19,31,46）。
[ICLR2017]
[19] Density estimation using Real NVP
https://arxiv.org/pdf/1605.08803.pdf [NeurIPS2018]
[31] Glow: generative flow with invertible 1× 1 convolutionshttps://arxiv.org/pdf/1807.03039.pdfhttps://arxiv.org/pdf/1807.03039.pdf [ECCV2020]
[46] Invertible image rescalinghttps://arxiv.org/pdf/2005.05650.pdf
Challenges in Denoising with Invertible Models
Applying invertible models in denoising is different from other applications. The widely used invertible networks employed in image generation [19, 31] and rescaling [46] consider the input and the reverted image to follow the same distribution. Such applications are straightforward candidates for invertible models. Image denoising, however, takes a noisy image as input and reconstructs a clean one, i.e., the input and the reverted outcome follow two different distributions. On the other hand, an invertible transform does not lose any information during the transformation. However, the lossless property of invertibility is not desired for image denoising since the noise information remains while we transform an input image into latent variables. If we can disentangle the noisy and clean signals during an invertible transformation, we may reconstruct a clean image without worrying about losing any important information by abandoning the noisy information. In the following section, we present one way to obtain a clean signal through an invertible transformation.
概括说，传统的可逆神经网络的输入和输出是一个东西，中间过程不丢失任何信息。但这个特征对于去噪有双面意义。一方面，去噪过程希望保持原图像一些重要信息，因此可逆神经网络的信息不丢失这个特点是优点。另一方面，因为去噪希望从噪声图像到干净图像，如果保持信息不丢失，那恢复的图像也带噪声，因此这个信息不丢失对于去噪有没有意义。
最后作者很巧妙的描述了这个过程，即做好特征解耦工作，将重要重构信息不丢失，同时将噪声信息去除。
Concept of Design
We denote the original noisy image as
, its clean version as
and the noise as
. We have:
. Using the invertible network, the learned latent representation of observation
初始建模：问题的简单描述。
On the other hand, invertible networks utilize different feature extraction approaches comparing with existing deep denoising models. Existing ones usually employ convolutional layers with padding to extract features. However, they are not invertible due to two reasons: Firstly, the padding makes the network non-invertible; secondly, the parameter matrices of convolutions may not be full-rank.
Thus, to ensure invertibility, rather than using convolutional layers, it is necessary to utilize invertible feature extraction methods, such as the Squeeze layer [31] and Haar Wavelet Transformation [7], as presented in Fig. 2. The Squeeze operation reshapes the input into feature maps with more channels according to a checkerboard pattern. Haar Wavelet Transformation extracts the average pooling of the original input as well as the vertical, horizontal, and diagonal derivatives. As a result, the spatial size of the feature maps extracted by the invertible methods is inevitably downscaled
阐述了为什么传统卷积不能作为特征提取方法：padding 和 非满秩参数矩阵，导致卷积不可逆。
介绍了两种可逆的特征提取方法：
Squeeze operation：将输入按照棋盘模式重塑为具有更多通道的特征映射；
Haar Wavelet Transformation：提取原始输入的平均池化以及垂直、水平和对角导数。
这样，用可逆方法提取的特征图的空间尺寸必然会缩小。
这段跟建模没关系。
[7] [2019]Guided image generation with ¨ conditional invertible neural networkshttps://arxiv.org/pdf/1907.02392.pdf
Therefore, instead of disentangling the clean and noisy signals directly, we aim to separate the low-resolution and high-frequency components of a noisy image. The sampling theory [22] indicates that during the downsampling process, the high-frequency signals are discarded. Since invertible networks are information-lossless [36], if we make the first three channels of the transformed latent representation to be the same as the downsampled clean image, high-frequency information will be encoded in the remaining channels. Based on the observation that the high-frequency information contains noise as well, we abandon all high-frequency representations before inversion to reconstruct a clean image from low-resolution components. We formally describe the process as follows:
where
represents the low-resolution clean image. We use
to represent the high-frequency contents that cannot be obtained by
to remove spatially variant noise completely. Nevertheless, a side-effect is the loss of
and train our invertible network to transform
, in conjunction with
由于不能用卷积，导致直接将图像解耦成干净成分和噪声成分不太可行。因此，作者将噪声图像分解为低频和高频成分，并认为噪声都包含在高频成分中。在重构图像时，高频成分就直接摒弃掉了。而干净图像从低频成分中进行重构。
但这样做最大的副作用就是高频成分中很重要的细节信息都被抛弃了。因此，在重构高频图像时，对 采样，训练可逆网络对 进行变换，结合 恢复干净图像 。这样，丢失的高频干净细节 被嵌入到潜在变量 中。
Network Architecture
We first employ a supervised approach to guide the network to separate high-frequency and low-resolution components during transformation. After some invertible transformation
, the noisy image
. We minimize the following forward objective
where
is the low-frequency components learned by the network, corresponding to three channels of the output representation in the forward pass.
is the number of pixels.
is the m-norm and
can be either 1 or 2. To obtain the ground truth low-resolution image
首先采用一种监督方法来引导网络在变换过程中分离高频和低分辨率分量。经过可逆变换，将噪声图像变换为对应的低分辨率干净图像和高频编码。这个过程的训练函数是公式（1）。
真实的低频成分 是通过对干净图像 双三次的转换得到的。
To restore the clean image with
with random variable
. The backward objective is written as
where
is the number of pixels. We train the invertible transformation
图像重构过程包括上一步训练的干净低频成分和从正态分布随机抽样变量 。
可逆变换 在正向和逆向过程同时训练。
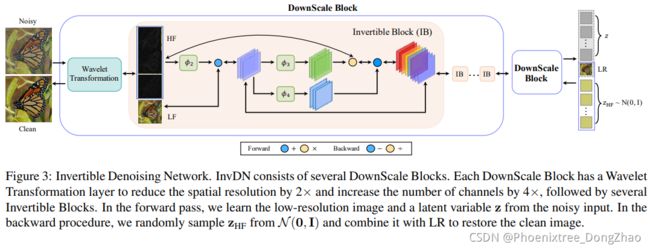
Inspired by [46, 7, 19], the invertible transform
网络的整体结构是：
1. 由若干 down-scale block 组成；
2. 每个 down-scale block 由一个 invertible wavelet transformation 后跟若干 invertible blocks 组成。
- Invertible Wavelet Transformation.
Since we aim to learn the low-resolution clean image in the forward pass, we apply invertible discrete wavelet transformations (DWTs), specifically Haar wavelet transformation, to increase feature channels and to down-sample feature maps. After the wavelet transformation, the input image or an intermediate feature map with the size of (H, W, C) is transformed into a new feature map of size (H/2, W/2, 4C). Haar wavelets decompose an input image into one low-frequency representation and three high-frequency representations in the vertical, horizontal, and diagonal direction [32]. Other DWTs can also be exploited, such as Haar, Daubechies, and Coiflet wavelets [46, 7].
可逆Haar小波变换，输入 (H, W, C)， 输出 (H/2, W/2, 4C)。分解为低频和 纵向、横向、对角线方向的高频分量。当然，也可以采用其他小波变换。
- Invertible Block.
The wavelet transformation layer in each down-scale block splits the representation into low- and high-frequency signals, which are further processed by a series of invertible blocks. The invertible block we follow in this work is the coupling layer [19]. Suppose the block’s input is
, and output is
. This block’s operations in the forward and backward pass are listed in Table 1.
Split(·) operation divides input feature map
and
, corresponding to the low-frequency image representations of size (H/2, W/2, C) and the high-frequency features (such as texture and noise) of size (H/2, W/2, 3C), respectively.
In R2 and R3 of Table 1, during the backward pass, only the Plus (+) and Multiply (⊙) operations are inverted to Minus (−) and Divide (/) while the operations performed by φ1 , φ2 , φ3 and φ4 are not required to be invertible（φ1并没有在图中出现）. Thus, φ1 , φ2 , φ3 and φ4 can be any networks, including convolutional layers with paddings. Since the skip connection is shown to be crucial for deep denoising networks [50, 51], we simplify the forward operation in R2 as
The low-frequency features can be passed to deep layers with this approach. We use the residual block as operations φ2 , φ3 and φ4 .
Concat(·) is the inverse operation of Split(·), which concatenates the feature maps along channels and passes them into the next module.
将表 1 和图 3 放在一起对比看：
本文采用的 invertible block 为 [19] 提出的耦合层 coupling layer。
具体结构如表 1 所示。
经过 Split(·) 操作，将输入 (H/2, W/2, 4C) 分解为低频 (H/2, W/2, C) 和高频 (H/2, W/2, 3C) 部分。
低频成分； 高频成分。
φ1 , φ2 , φ3 and φ4 不参与可逆过程，故可以采用卷积层实现。其中 φ2 , φ3 and φ4 为残差网络。
从 R2 和 R3 可以看出，i+1 层的低频成分是上一层低频和高频成分共同得到；而 i+1 层高频成分，只来自于上一层低频成分。
Concat(·) 是 Split(·) 的逆过程。
核心 Code
import math
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
class InvBlockExp(nn.Module):
def __init__(self, subnet_constructor, channel_num, channel_split_num, clamp=1.):
super(InvBlockExp, self).__init__()
self.split_len1 = channel_split_num
self.split_len2 = channel_num - channel_split_num
self.clamp = clamp
self.F = subnet_constructor(self.split_len2, self.split_len1)
self.G = subnet_constructor(self.split_len1, self.split_len2)
self.H = subnet_constructor(self.split_len1, self.split_len2)
def forward(self, x, rev=False):
x1, x2 = (x.narrow(1, 0, self.split_len1), x.narrow(1, self.split_len1, self.split_len2))
if not rev:
y1 = x1 + self.F(x2)
self.s = self.clamp * (torch.sigmoid(self.H(y1)) * 2 - 1)
y2 = x2.mul(torch.exp(self.s)) + self.G(y1)
else:
self.s = self.clamp * (torch.sigmoid(self.H(x1)) * 2 - 1)
y2 = (x2 - self.G(x1)).div(torch.exp(self.s))
y1 = x1 - self.F(y2)
return torch.cat((y1, y2), 1)
def jacobian(self, x, rev=False):
if not rev:
jac = torch.sum(self.s)
else:
jac = -torch.sum(self.s)
return jac / x.shape[0]
class HaarDownsampling(nn.Module):
def __init__(self, channel_in):
super(HaarDownsampling, self).__init__()
self.channel_in = channel_in
self.haar_weights = torch.ones(4, 1, 2, 2)
self.haar_weights[1, 0, 0, 1] = -1
self.haar_weights[1, 0, 1, 1] = -1
self.haar_weights[2, 0, 1, 0] = -1
self.haar_weights[2, 0, 1, 1] = -1
self.haar_weights[3, 0, 1, 0] = -1
self.haar_weights[3, 0, 0, 1] = -1
self.haar_weights = torch.cat([self.haar_weights] * self.channel_in, 0)
self.haar_weights = nn.Parameter(self.haar_weights)
self.haar_weights.requires_grad = False
def forward(self, x, rev=False):
if not rev:
self.elements = x.shape[1] * x.shape[2] * x.shape[3]
self.last_jac = self.elements / 4 * np.log(1/16.)
out = F.conv2d(x, self.haar_weights, bias=None, stride=2, groups=self.channel_in) / 4.0
out = out.reshape([x.shape[0], self.channel_in, 4, x.shape[2] // 2, x.shape[3] // 2])
out = torch.transpose(out, 1, 2)
out = out.reshape([x.shape[0], self.channel_in * 4, x.shape[2] // 2, x.shape[3] // 2])
return out
else:
self.elements = x.shape[1] * x.shape[2] * x.shape[3]
self.last_jac = self.elements / 4 * np.log(16.)
out = x.reshape([x.shape[0], 4, self.channel_in, x.shape[2], x.shape[3]])
out = torch.transpose(out, 1, 2)
out = out.reshape([x.shape[0], self.channel_in * 4, x.shape[2], x.shape[3]])
return F.conv_transpose2d(out, self.haar_weights, bias=None, stride=2, groups = self.channel_in)
def jacobian(self, x, rev=False):
return self.last_jac
class InvNet(nn.Module):
def __init__(self, channel_in=3, channel_out=3, subnet_constructor=None, block_num=[], down_num=2):
super(InvNet, self).__init__()
operations = []
current_channel = channel_in
for i in range(down_num):
b = HaarDownsampling(current_channel)
operations.append(b)
current_channel *= 4
for j in range(block_num[i]):
b = InvBlockExp(subnet_constructor, current_channel, channel_out)
operations.append(b)
self.operations = nn.ModuleList(operations)
def forward(self, x, rev=False, cal_jacobian=False):
out = x
jacobian = 0
if not rev:
for op in self.operations:
out = op.forward(out, rev)
if cal_jacobian:
jacobian += op.jacobian(out, rev)
else:
for op in reversed(self.operations):
out = op.forward(out, rev)
if cal_jacobian:
jacobian += op.jacobian(out, rev)
if cal_jacobian:
return out, jacobian
else:
return out