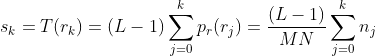灰度变换与空间滤波

前言：空间域指图像平面本身，这类图像处理方法直接以图像中的像素操作为基础。这是相对于变换域中的图像处理而言的，变换域的图像处理首先把一幅图像变换到变换域，在变换域中进行处理，然后通过反变换把处理结果返回到空间域。空间域主要分为灰度变换和空间滤波两类。

一、背景知识

1、灰度变换和空间滤波基础

空间域就是简单的包含图像像素的平面，与频率域相反，空间域技术直接在图像像素上操作。空间域处理可由下式表示：，其中是输入图像，是处理后的图像，是在点的邻域上定义的关于的一种算子。算子可应用于单幅图像或图像集合，为降低噪声而对图像序列执行逐像素的求和操作。

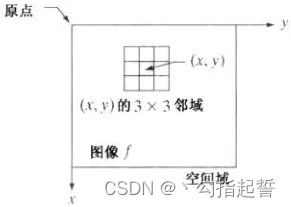
 上图显示了公示在单幅图像上的基本实现，图中的点是图像中的一个任意位置，包含该点的小区域是点的邻域，典型的，邻域是中心在的矩形，其尺寸比图像小得多。 

二、基本的灰度变换函数

 1、图像反转

使用上图中所示的反转变换，可得到灰度级范围为的一幅图像的反转图像，该反转图像由下式给出：，使用这种方式反转一幅图像的灰度级，可得到等效的照片底片。这种类型的处理特别适用于增强嵌入在一幅图像的暗区域中的白色或灰色细节。

2、对数变换

对数变换的通用形式为：，其中是一个常数，并假设。图中对数曲线的形状表明，该变换将输入中范围较窄的低灰度值映射为输出较宽范围的灰度值，相反地，对高的输入灰度值也是如此。

3、幂律（伽马）变换

幂律变换的基本形式为：，其中和为正常数。有时考虑偏移量（即输入为0时的一个可度量输出），该式也写为。然而，偏移量一般是个显示标定问题，因而作为一个结果，通常忽略不计。对于不同的值，与的关系如下图所示。

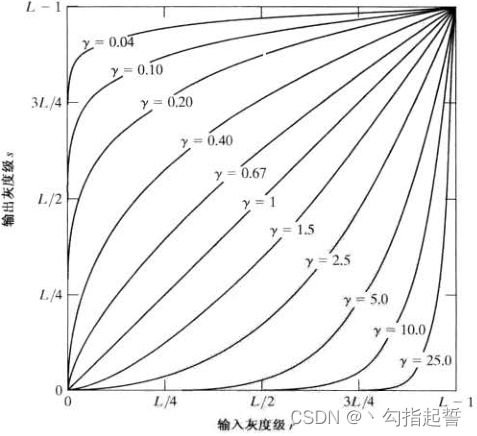
 与对数变换的情况类似，部分值的幂律曲线将较窄范围的暗色输入值映射为较宽范围的输出值，相反地，对于输出高灰度值时也成立。然而，与对数函数不同的是，我们注意到，随着值的变化，将简单地得到一族可能的变换曲线。正如所预期的那样，在图中，的值所生成的曲线和的值所生成的曲线的效果完全相反。最后，在时简化成了恒等变换。

三、直方图处理

1、直方图均衡变换函数

变换的离散形式为：，其中

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

"""
*    Function:            计算新灰度值数组
*    parameter:        
*        pixels           原始像素数组
*    return: 
"""

def getHistogram(pixels):
    GrayValuesCounts = np.zeros(256)
    for rows in pixels:
        for value in rows:
            GrayValuesCounts[value] = GrayValuesCounts[value] + 1
    #data = range(0, 256)
    #if isDisplsy:
    #    plt.bar(data, GrayValuesCounts)
    #    plt.show()

    return GrayValuesCounts

def getGrayValuesChange(pixels):
    sp = pixels.shape
    GrayValuesCounts = getHistogram(pixels)

    temps = np.zeros(256)
    for i in range(0, len(temps)):
        for j in range(0, i + 1):
            temps[i] += 255.0 * GrayValuesCounts[j] / (sp[0] * sp[1])

    return np.round(temps)

"""
*    Function:                  灰度均衡函数
*    parameter:        
*        pixels                 原始像素数组
*        grayValuesNew          灰度值数组
"""
def grayEqualize(str, grayValuesNew):
    out = str
    sp = str.shape

    for i in range(0, sp[0]):
        for j in range(0, sp[1]):
            out[i][j] = grayValuesNew[str[i][j]]

    return out

if __name__ == '__main__':
    pic = cv.imread('picture/histogram.png', 0)

    grayValuesNew = getGrayValuesChange(pic)
    data = range(0, 256)

    plt.subplot(2, 2, 1)
    plt.imshow(pic, cmap='gray')

    plt.subplot(2, 2, 2)
    plt.bar(data, getHistogram(pic))

    imag = grayEqualize(pic, grayValuesNew)

    plt.subplot(2, 2, 3)
    plt.imshow(imag, cmap='gray')

    plt.subplot(2, 2, 4)
    plt.bar(data, getHistogram(imag))

    plt.show()

2、局部直方图处理

全局直方图处理可能会导致增强图像中小区域的细节被忽略。解决方法是以图像中每个像素的领域中的灰度分布为基础设计变换函数。

3、图像增强中使用直方图统计

直接从直方图获得的统计参数可用于图像增强。令表示在区间上代表灰度值的一个离散随机变量，并令表示对应于值的归一化直方图分量。可以把看成是得到直方图的那幅图像的灰度出现的概率的估计。

关于均值的阶矩定义为：，其中，是的均值（平均灰度，即图像中像素的平均灰度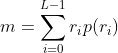）：，二阶矩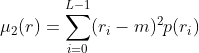：，该表达式称为灰度方差，通常用表示。均值是平均灰度的度量，方差（或标准差）是图像对比度的度量。一旦从给定的图像得到了直方图，用前边的表达式就很容易计算所有的矩。

四、空间滤波基础

“滤波”是指接受（通过）或拒绝一定的频率分量。例如，通过低频的滤波器称为低通滤波器。低通滤波器的作用是通过模糊图像来平滑图像。使用空间滤波器可以直接对图像本身进行类似的平滑处理。空间滤波通过把每个像素的值替换为该像素及其邻域的函数值来修改图像。如果对图像像素执行的运算是线性的，那么称该滤波器为线性空间滤波器。否则，称该滤波器为非线性空间滤波器。

1、空间滤波机理

线性空间滤波器在图像和滤波器核之间执行乘机之和运算。核是一个阵列，其大小定义了运算的邻域，其系数决定了该滤波器的性质。

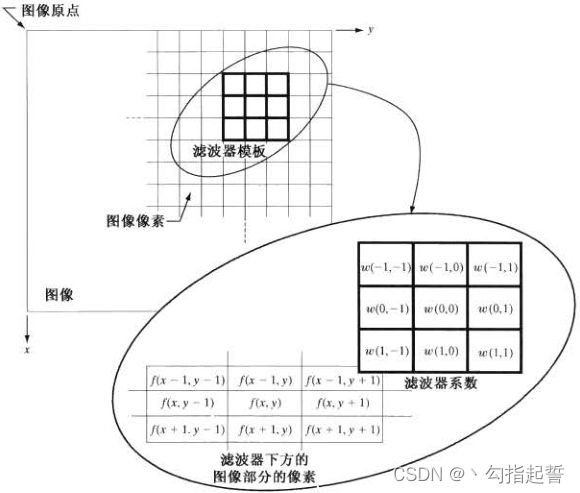
上图说明了使用核进行线性空间滤波的原理，在图像中的任何一点处，滤波器的响应是核系数核核所覆盖图像像素的乘积之和。坐标和变化时，核的中心逐个像素地移动，并在移动过程中生成滤波后的图像(通常不覆盖原图像，而是新建图像)。

2、空间相关与卷积

根据上图中空间相关的图形说明，其数学描述为：

相关的运算过程如下：在图像上移动核的中心，并且在每个位置计算乘积之和。空间卷积的原理相同，只是把相关运算的核旋转180°。因此当核的值关于其中心对称时，相关核卷积得到的结果相同。在我们用滤波器核去扫描图像f时，会发现的一部分在之外，发现求和在这个区域未定义，其中一个解决办法时在的两侧补足够多的，一般来说，如果核的大小为1xm，那么为了处理相对于的起始结构核结束结构，的两侧都需要补个0。核与一个（1个元素是1，其他元素是0）函数相关时，将得到的一个副本，但这个副本旋转了180°。这个函数，即一个元素时1，其余元素是0函数，称为离散单位冲激函数。核与离散单位冲激函数相关时，会在这个冲激的位置产生核的旋转版本。（这里“冲激的位置”可以理解为滤波器核中心与冲激函数匹配的位置，即冲激函数被扫描的位置）

卷积和相关唯一的不同是在执行移位/乘积之和前，核预先旋转了180°。预先旋转核的作用是，现在在单位冲激的位置我们已有核的一个准确副本（卷积结果是原w的一个准确副本，即未旋转的核w)事实上，线性系统理论的基础是将一个函数与一个冲激进行卷积，在冲激所在的位置产生这个函数的一个副本。（频率域滤波会广泛使用这个性质）刚才讨论的一维概念很容易推广到图像，对于大小为mxn的核，我们在图像的顶部和底部分别至少补(m-1)/2行0，在图像的左侧和右侧分别至少补(n-1)/2列0。这里补正的0的个数很好理解，零的个数由核的对半开的侧翼扁平的零个数决定，比如一维的核，去除中间数，侧翼的零的个数即需要补正的零的个数（核从中间数开始扫描），二维核同理。

由上图可以看到，函数与冲激的卷积把函数复制到了冲激所在的位置，若核的值关于核中心对称，则相关核卷积的结果相同。在二维情况下，旋转180°等效于核关于其一个轴翻转，然后关于另一个轴翻转，这里轴指通过核中心点的竖轴和横轴。