抽样（蒙特卡洛法）到底是在干啥？
目录
一、简单抽样
二、逆转换方法
三、“接受-拒绝”抽样
四、马尔科夫链蒙特卡洛法（MCMC）
五、 “接受-拒绝”抽样再认识
1. 接受-拒绝抽样法理论介绍
2. 算法
3. 接受-拒绝抽样法代码实现
六、马尔科夫链蒙特卡洛法（MCMC）的再认识
1. 马尔科夫链的一些性质
2.马尔科夫链蒙特卡洛法理论介绍
七、Metropolis-Hastings算法（MH算法）
1.MH算法理论介绍
2. 算法
八、吉布斯抽样
1. Gibbs算法理论介绍
2. 算法
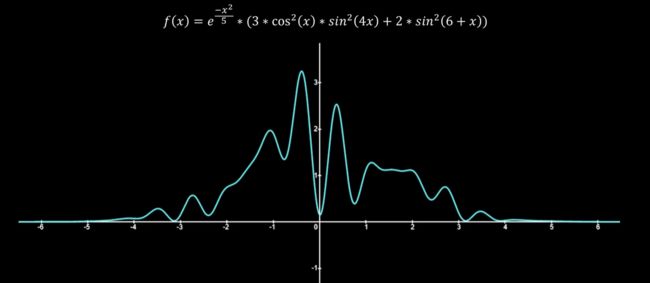
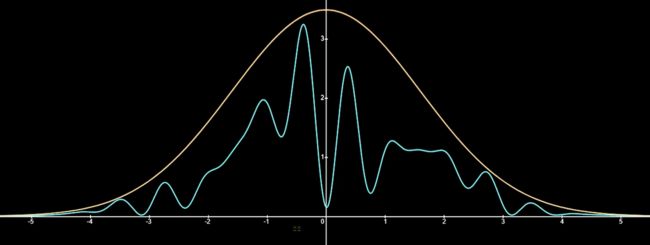
最近在学马尔可夫蒙特卡洛法，期间学习了各种各样的抽样方法，也在《概率图模型基于R》这本书中看到了一些代码实现，但是说实话我都还没搞清楚抽样到底是在干什么。昨天在B站关注到一位UP主（FunInCode）感觉讲的很不错，这里按照下图的分布我解释一下抽样到底是在干什么。
因为我的统计基础薄弱，所以很多基础概念都不扎实。之前我看f(x)，就觉得这就是一个函数，抽样是不是就是从这个函数上取点？随机抽样是不是就是随机在这个函数上取点？那比如说上面这个函数的定义域是（-5，5），那我直接在（-5，5）上随机取一个点x，然后求对应的函数点(x,f(x))不就好了吗，干嘛整那么复杂？
实际上，我们抽样是这个意思：f(x)是一个函数没错，但是它是一个分布函数，我不是要在f(x)上取点。f(x)描绘的是一个模型在（-5，5）上的取值概率，显然这个模型取-5和5附近的值要远小于-0.5和0.5附近的值的概率。抽样要满足的就是你到时候在x轴上取过来的点，0.5和-0.5附近取到的多一点，5和-5附近取到的点少一点，满足分布函数描述的事实。
接下来具体讲几个抽样：
（以下图片和例子都是来自于 （FunInCode）的视频。有部分内容参考了《概率图模型基于R》和《统计学习方法》）
一、简单抽样
（0，1）上的均匀分布，直接在（0，1）上产生随机数就好啦
二、逆转换方法
现在我要按照指数分布f(x)进行抽样，用的方法是逆转换方法。
例子：将均匀分布转换为指数分布
设：a是在（0，1）上随机取的值，T(·)是转换函数，F(·)是指数函数的累积分布函数，则
假设T(·)的单调性满足
因此，
那么将a从均匀分布转换为指数分布的转换函数T(a)就可以用指数分布的累积分布函数CDF的反函数来表示了。
通过上述的过程，我们也发现这个方法的两个缺点就是需要求目标函数的CDF（累积分布函数，这里涉及到求和或积分）及其反函数。
三、“接受-拒绝”抽样
“接受-拒绝”抽样其实并不复杂，我之前看书上的推导的时候也感觉没什么太大的难度，但是我在看了B站UP主 （FunInCode）的视频后真的是醍醐灌顶。
不过在学习一个更复杂的方法之前，我们必要要思考的问题就是学习这个方法的必要性：逆转换方法的两个缺点导致过程过于复杂甚至不可进行。
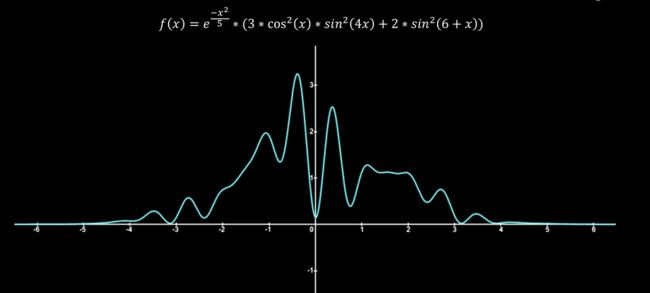
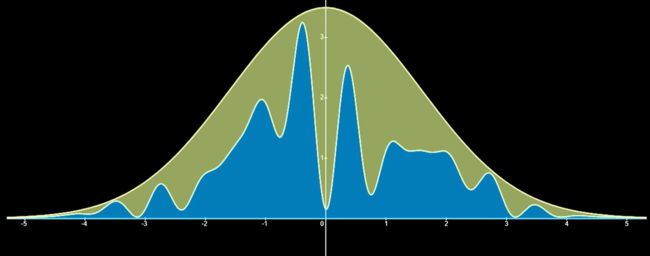
我们结合下图来讲解“接受-拒绝”抽样
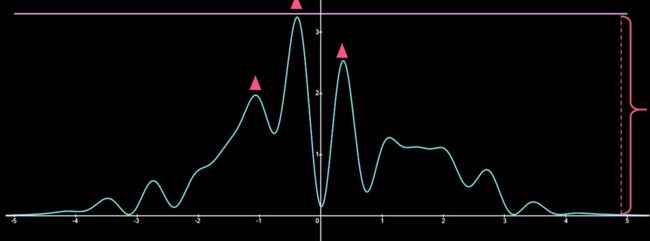
为了表达方便，我们假设f(x)的定义域为（-5，5），函数靠近y轴的三个极大值点分别为（-1，2）、（-0.5，3.2）和（0.5，2.5）。为了得到满足f(x)分布的抽样样本，我们就得想办法让抽样的值在-1，-0.5和0.5附近比较多，其中-0.5处应该最多。怎么去实现呢？
我们还是在整个定义域（-5，5）上均匀取值，如果取到的值是在-1，-0.5和0.5附近的话，就大概率接受你，反之，就更倾向于拒绝。
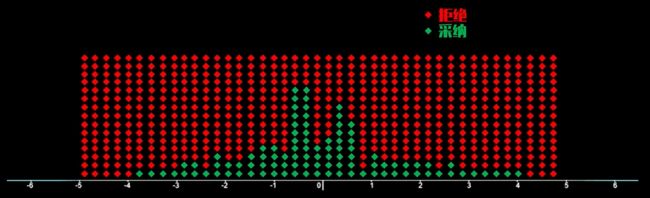
图中的小方块就是在（-5，5）上的均匀取值。然后每一点是接受还是拒绝依赖于f(x)的大小。
接下来我们就要思考接受和拒绝的规则是什么了
我们在函数上方取一个常值函数，不妨是y=3.5，接下来对于每一个服从（-5，5）上均匀分布的点x，根据
的概率进行接受或拒绝。具体的，就是将f(x)与服从（0，3.5）上均匀分布的随机抽样值b进行比较，如果f(x)>b，就接受；反之，拒绝。
我们需要注意两件事：
- 第一，我们取得y=3.5满足的条件是该函数的每一点处的函数值都大于对应f(x)的值，也就是说我们取的函数要在f(x)上面。
- 第二，我们是在（-5，5）上均匀取值，然后再按照规则去接受或拒绝，虽然取得点足够多的时候总是可以达成目标的，但是效率不高，因此我们有比较把“在（-5，5）上均匀取值”改成“更大的可能性取在-1、-0.5和0.5这样的点附近处，而更少的取在-5，5这样的点附近”
所以，我们按照下面的正态分布再取值
这里我们一定要搞清楚正态分布在这里是干吗用的
- 第一，我们想要取的是满足f(x)的样本，但是我们现在是按照正态分布来取的
- 第二，正态分布起到了上面那个例子中y=3.5的作用。我们按照正态分布取点a后，将a和服从（0，g(a)）（g(x)指的是正态分布的PDF）上的均匀分布的随机抽样值b进行比较，如果f(x)>b，就接受；反之，拒绝。
我们一定要明白的是：之所以引入上述的正态分布是为了把效率提高。我再重复一遍我们已知的，下图中的蓝色是接受区域，而绿色的是拒绝区域，而这只是二维的图像，当维数变大时，这个绿色区域的占比会显著提升，这也就意味着我们取值的效率很低。
讲到这个方法在某些情况下效率低就意味着我们要去研究另一种可以克服这种缺点的方法，这就是我们下面要介绍的马尔科夫链蒙特卡洛法（MCMC）。
四、马尔科夫链蒙特卡洛法（MCMC）
我们还是得再讲一下“接受-拒绝”抽样，因为MCMC算法就是对“接受-拒绝”抽样的一个改进。
之前我们用正态分布来进行最初的抽样，这个抽样它是没有“记性”的。我们再次回顾一下，我们抽样是要干什么？就是在f(x)大处取更多的点，在f(x)小处取更少的点，使得最后样本的分布正好是f(x)的样子。也就是说我们应当在-1处取更多的点，但是我们每次实际上都是按正态分布来取值的。我现在按照正态分布正好在-1处取到了一点，我以较大的概率正好也被接受了，那我接下来应该记住这个信息：应该在这一点（x=-1）附近取更多的点。但是正态分布不管这些细节，它只知道要在y轴附近取更多的点，不会知道要在-1处取更多的点。
现在问大家，怎么才能在我已经知道了f(-1)很大，也就是我应该在-1附近取更多的点的情况下，把这个信息传达给正态分布并在接下来的抽样中体现呢。
对了，就是说：我知道-1处应该取更多的点，我就和正态分布说，你往左边挪一步。那么状态分布就调整到以x=-1为对称轴的情况了，那接下来我按照这个挪一步后的正态分布去抽样，是不是就符合我的要求了。
上述说明下一步的正态分布要参考这一步我知道的信息，这就是马尔科夫链的知识。在这里我们提出蒙特卡洛法的定义：
按抽样调查法求取统计值来推定未知特性量的计算方法。
所以，我们上面介绍的这些都叫做蒙特卡洛法。现在我们要把这些个方法用马尔科夫链的知识进行改造，得到的方法就叫马尔科夫链蒙特卡洛法（MCMC）。
到目前为止，我们并没有用晦涩的数学公式来讲解，为的是把这些方法讲的通俗易懂一点，然而想要真正的了解它们的构造，数学表达是必不可少的。
五、 “接受-拒绝”抽样再认识
1. 接受-拒绝抽样法理论介绍
假设有随机变量x，取值x∈X,其概率密度函数为p(x)。目标是得到该概率分布的随机样本，以对这个概率分布进行分析。
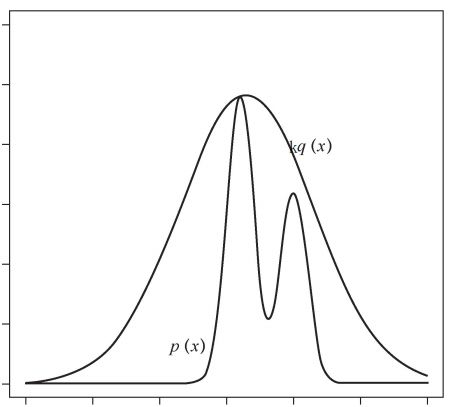
接受拒绝法的基本想法如下：假设p(x)不可以直接抽样。找一个可以直接抽样的分布，称为建议分布。假设q(x)是建议分布的概率密度函数，并且有q(x)的k倍一定大于等于p(x),其中k>0,如图所示。
按照q(x)进行抽样，假设得到结果是x*,再按照
的比例随机决定是否接受x*。直观上，落到p(x*)范围内的就接受，落到p(x*)范围外的就拒绝。接受拒绝法实际是按照p(x)的涵盖面积（或涵盖体积）占kq(x)的涵盖面积（或涵盖体积)的比例进行抽样。
2. 算法
算法（接受-拒绝法）
输入：抽样的目标概率分布的概率密度函数p(x)；
输出：概率分布的随机样本。
参数：样本数n
(1)选择概率密度函数为q(x)的概率分布，作为建议分布，使其对任一x满足kq(x)≥p(x)，其中k>0。
(2)按照建议分布q(x)随机抽样得到样本x*,再按照均匀分布在(0,1)范围内抽样得到u。
(3)如果
则将x*作为抽样结果；否则，回到步骤(2)。
(4)直至得到n个随机样本，结束。
接受拒绝法的优点是容易实现，缺点是效率可能不高。如果p(x)的涵盖体积占kq(x)的涵盖体积的比例很低，就会导致拒绝的比例很高，抽样效率很低。注意，一般是在高维空间进行抽样，即使p(x)与kq(x)很接近，两者涵盖体积的差异也可能很大（与我们在三维空间的直观不同）。
3. 接受-拒绝抽样法代码实现
下图中红线是建议分布，黑线目标分布。
# N：样本数
# k：建议分布的系数
# p：要估计的分布
# q：建议分布
# rq：建议分布的采样器
rejection <-function(N,k,p,q,rq) #拒绝算法
{
accept <-logical(N) #生成N个FALSE
x <-numeric(N) #生成N个0
for(i in 1:N)
{
z0 <-rq() #从建议分布中取出一点
u0 <-runif(1,0,1) #从0-1的均匀分布上取一点
if(u0 以上内容来自我的这篇博客
六、马尔科夫链蒙特卡洛法（MCMC）的再认识
之前我们说过MCMC算法的感觉就是：正态分布估计我现在已知的信息向左挪了一步，现在考虑一般的情况。不过在此之前我们先了解一下马尔科夫链的一些性质，只要了解即可。
1. 马尔科夫链的一些性质
定义 马尔科夫链
考虑一个随机变量的序列
这里
表示时刻t的随机变量，每个随机变量的取值集合相同，称为状态空间。的概率分布为
。如果只依赖于
，而不依赖于过去的随机变量，这一性质成为马尔可夫性。
定义 转移矩阵 离散
马尔科夫链的转移概率为
可由矩阵表示，即
其中
定义 转移核 连续
连续马尔科夫链，随机变量
定义在连续状态空间S，转移概率分布由转移核表示。
设S是连续状态空间，对任意的
，转移核
定义为
其中
是概率密度函数，满足
，
。转移核表示从
的转移概率
有时也将概率密度函数称为转移核。
定义 细致平衡
设有马尔科夫链，状态空间为S，转移概率矩阵为P，如果有状态分布
，对于容易状态
，对任意时刻 t 满足
或者简写为
定理 细致平衡方程
满足细致平衡方程的状态分布
就是该马尔科夫链的唯一平稳分布，即
2.马尔科夫链蒙特卡洛法理论介绍
如果满足细致平衡方程，那方程中的状态分布就是平稳分布。如果平稳分布就是我们关注的目标分布的话，那马尔可夫链
的分布会收敛到该平稳分布，因此我们关注马尔科夫链即可。
在此之前，我们要区分一下几个概念：
是目标分布；可以用我们最开始讲的函数
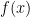来理解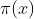
是目标平稳分布；
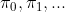收敛到也就是我们的目标分布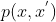
是转移核；
如果假设马尔科夫链满足细致平衡方程，那么该马尔科夫链是平稳的，有唯一的平稳分布，设为我们的目标函数
则由细致平衡方程知
其中是转移核，也就是我们在马尔科夫链上制定的规则，我们接下来就要去找出这个规则具体是什么。
我们并不知道关于的一点信息，所以我们另外找了一个清楚明了的建议分布
。尽管我们对建议分布了解的程度更高，但是往往以下等式并不成立
也就是说
现在，考虑在等式两边加上一些东西使等式成立
其中
令
那么就有
实际上我们得出来的这条等式在上面也出现过，不过区别是现在我们知道每一项的具体含义。称为建议分布，
称为接受分布。注意接受指的是接受转移。
我们也应当理解表达的内涵。也就是说，基于我目前的状态
，接下来转化为
的概率由
来表示。实际上建议分布我们是清楚的，所以目前不清楚的只剩下接受分布了。
之所以后面还需要介绍一个算法就意味这MCMC算法还存在缺点。也就是当非常小时，这个算法的效率是非常低的。
七、Metropolis-Hastings算法（MH算法）
1.MH算法理论介绍
非常小怎么办呢，我们要关注第一次出现是在哪里：
我们可以把上式中的和
同时扩大，既不影响等式，又把接受概率变大了，使模型效率增大。那么具体扩大多少倍呢？扩大到使得
=1为止，不妨假设扩大到
。为了简便，我们扩大后的项仍写作原样，但是读者要注意，我们实际上已经扩大了一定的倍数。因此，仍然是
其中，
则
以上结论是在假设扩大到的情况下得出来的，更一般的有
若
则
2. 算法
输入：抽样的目标分布的密度函数，函数
输出：的随机样本
参数：收敛步数m，迭代步数n
（1）任意选择一个初始值
（2）对
循环执行
（a）设状态
，按照建议分布随机抽取一个候选状态
（b）计算接受概率
（c）从区间(0,1)中按均匀分布随机抽取一个数
若
，则状态
；否则，状态
八、吉布斯抽样
最后我们介绍MH算法的特殊情况——Gibbs抽样。
1. Gibbs算法理论介绍
定义 满条件
马尔可夫链蒙特卡罗法的目标分布通常是多元联合概率分布
，其中
为k维随机变量。如果条件概率分布
中所有k个变量全部出现，其中
，
，那么称这种条件概率分布为满条件分布。
吉布斯抽样是单分量 Meropolis-Hastings 算法的特殊情况。定义建议分布是当前变量
的满条件分布
对于上式的理解，我们应当要理解到：
因此，有
故
另外，我没注意：
2. 算法
算法（吉布斯抽样）
输入：目标概率分布的密度函数，函数
输出：的随机样本
参数：收敛步数m，迭代步数n
（1）初始化。给出初始样本
（2）对
循环执行
设第
次迭代结束时的样本为
，则第次迭代进行如下几步操作：
（1）由满条件分布
抽取
...
（ j ）由满条件分布
抽取
...
（ k ）由满条件分布
抽取
得到第 i 次迭代值