各种 NMS

---

经典NMS

实现步骤如下：

1. 选取这类output bbox中scores（置信度）最大的哪一个，记为bbox_best，并保留它
2. 计算bbox_best与其余的bbox的IOU
3. 如果其IOU>0.5了，那么就舍弃这个bbox（由于可能这两个box表示同一目标，所以保留分数高的哪一个）
4. 从最后剩余的bboxes中，再找出最大scores的哪一个，如此循环往复

import numpy as np

def nms(dets,thresh):
    #首先为x1,y1,x2,y2,score赋值
    x1 = dets[:,0]              #取所有行第一列的数据
    y1 = dets[:,1]
    x2 = dets[:,2]
    y2 = dets[:,3]
    scores = dets[:,4]

    #按照score的置信度将其排序,argsort()函数是将x中的元素从小到大排列，提取其对应的index(索引)
    order = scores.argsort()[::-1]
    #计算面积
    areas = (x2-x1+1)*(y2-y1+1)

    #保留最后需要保留的边框的索引
    keep = []
    while order.size > 0:
        #order[0]是目前置信度最大的，肯定保留
        i = order[0]
        keep.append(i)
        #计算窗口i与其他窗口的交叠的面积，此处的maximum是np中的广播机制
        xx1 = np.maximum(x1[i],x1[order[1:]])
        yy1 = np.maximum(y1[i],y1[order[1:]])
        xx2 = np.minimum(x2[i],x2[order[1:]])
        yy2 = np.minimum(y2[i],y2[order[1:]])

        #计算相交框的面积,左上右下，画图理解。注意矩形框不相交时w或h算出来会是负数，用0代替
        w = np.maximum(0.0,xx2-xx1+1)
        h = np.maximum(0.0,yy2-yy1+1)
        inter = w*h

        #计算IOU：相交的面积/相并的面积
        ovr = inter/(areas[i]+areas[order[1:]]-inter)

        #inds为所有与窗口i的iou值小于threshold值的窗口的index，其他窗口此次都被窗口i吸收
        inds = np.where(ovr<thresh)[0]                  #np.where就可以得到索引值(3,0,8)之类的，再取第一个索引
        #将order序列更新，由于前面得到的矩形框索引要比矩形框在原order序列中的索引小1（因为计算inter时是少了1的），所以要把这个1加回来
        order = order[inds+1]

    return keep

# test
if __name__ == "__main__":
    dets = np.array([[30, 20, 230, 200, 1],
                     [50, 50, 260, 220, 0.9],
                     [210, 30, 420, 5, 0.8],
                     [430, 280, 460, 360, 0.7]])
    thresh = 0.35
    keep_dets = nms(dets, thresh)
    print(keep_dets)
    print(dets[keep_dets])

适应范围：
标准的NMS一般用于轴对齐的矩形框（即水平bbox）

缺点：
顺序处理的模式，计算IoU拖累了运算效率。剔除机制太严格，依据NMS阈值暴力剔除。阈值是经验选取的。评判标准是IoU，即只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面。

Soft-NMS

经典NMS算法存在着一些问题：1、对于重叠物体无法很好的检测。当图像中存在两个重叠度很高的物体时，经典NMS会过滤掉其中置信度较低的一个。2、不要粗鲁地删除所有IOU大于阈值的框，而是降低其置信度。
其中红色框为经典NMS的步骤，而绿色框中的内容为Soft-NMS改进的步骤。Soft-NMS是使用一个基于Iou的衰减函数，降低Iou大于阈值Nt的Bounding box的置信度，IoU越大，置信度衰减程度越大。

import numpy as np
import copy


def soft_nms(bboxes, Nt=0.3, sigma2=0.5, score_thresh=0.3, method=2):
    # 在 bboxes 之后添加对于的下标[0, 1, 2...], 最终 bboxes 的 shape 为 [n, 5], 前四个为坐标, 后一个为下标
    res_bboxes = copy.deepcopy(bboxes)
    N = bboxes.shape[0]  # 总的 box 的数量
    indexes = np.array([np.arange(N)])  # 下标: 0, 1, 2, ..., n-1
    bboxes = np.concatenate((bboxes, indexes.T), axis=1)  # concatenate 之后, bboxes 的操作不会对外部变量产生影响
    # 计算每个 box 的面积
    x1 = bboxes[:, 0]
    y1 = bboxes[:, 1]
    x2 = bboxes[:, 2]
    y2 = bboxes[:, 3]
    scores = bboxes[:, 4]
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)

    for i in range(N):
        # 找出 i 后面的最大 score 及其下标
        pos = i + 1
        if i != N - 1:
            maxscore = np.max(scores[pos:], axis=0)
            maxpos = np.argmax(scores[pos:], axis=0)
        else:
            maxscore = scores[-1]
            maxpos = 0
        # 如果当前 i 的得分小于后面的最大 score, 则与之交换, 确保 i 上的 score 最大
        if scores[i] < maxscore:
            bboxes[[i, maxpos + i + 1]] = bboxes[[maxpos + i + 1, i]]
            scores[[i, maxpos + i + 1]] = scores[[maxpos + i + 1, i]]
            areas[[i, maxpos + i + 1]] = areas[[maxpos + i + 1, i]]
        # IoU calculate
        xx1 = np.maximum(bboxes[i, 0], bboxes[pos:, 0])
        yy1 = np.maximum(bboxes[i, 1], bboxes[pos:, 1])
        xx2 = np.minimum(bboxes[i, 2], bboxes[pos:, 2])
        yy2 = np.minimum(bboxes[i, 3], bboxes[pos:, 3])
        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        intersection = w * h
        iou = intersection / (areas[i] + areas[pos:] - intersection)
        # Three methods: 1.linear 2.gaussian 3.original NMS
        if method == 1:  # linear 加权
            weight = np.ones(iou.shape)
            weight[iou > Nt] = weight[iou > Nt] - iou[iou > Nt]
        elif method == 2:  # gaussian 加权
            weight = np.exp(-(iou * iou) / sigma2)
        else:  # original NMS
            weight = np.ones(iou.shape)
            weight[iou > Nt] = 0
        scores[pos:] = weight * scores[pos:]
    # select the boxes and keep the corresponding indexes
    inds = bboxes[:, 5][scores > score_thresh]
    keep = inds.astype(int)
    return res_bboxes[keep]


if __name__ == "__main__":
    dets = np.array([[665, 979, 1310, 2041, 0.94],
                     [741, 930, 1438, 1903, 0.6],
                     [582, 1065, 1417, 2079, 0.743],
                     [527, 1186, 1365, 1910, 0.643],
                     [703, 1092, 1241, 2092, 0.732],
                     [500, 1424, 1262, 2203, 0.475],
                     [645, 920, 1389, 1727, 0.375]])
    print(soft_nms(bboxes=dets))

Softer-NMS(CVPR 2019)

无论是经典NMS还是Soft-NMS算法，都是在一种假设前提下：置信度最高的Bounding box就是目标的候选位置最精确的物体位置。但是事实上，这个假设可能并不成立，或者说并不那么精确。NMS时用到的score仅仅是分类置信度得分，不能反映Bounding box的定位精准度，既分类置信度和定位置信非正相关的。NMS只能解决分类置信度和定位置信度都很高的，但是对其它三种类型：“分类置信度低-定位置信度低”，“分类置信度高-定位置信度低”，“分类置信度低-定位置信度高“都无法解决。

所有的候选Bounding box都够精确，无法确定该选择哪一个，见图7a

具有高置信度的Bounding box不够精确，见图7b

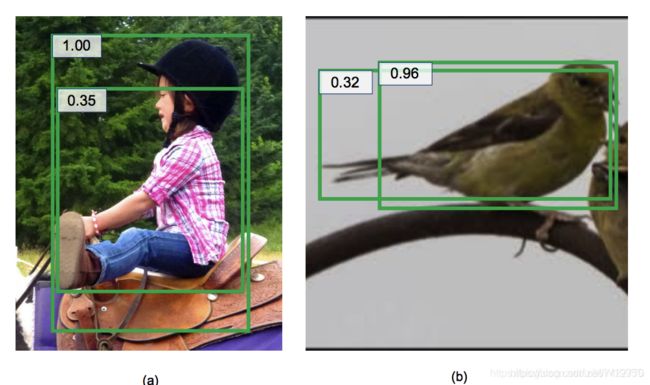代码：https://github.com/yihui-he/softer-NMS

DIoU-NMS (AAAI 2020)

DIoU-NMS出现于Distance-IoU一文，研究者认为若相邻框的中心点越靠近当前最大得分框 M 的中心点，则其更有可能是冗余框。也就是说，考虑IoU相同的情况，如下所示
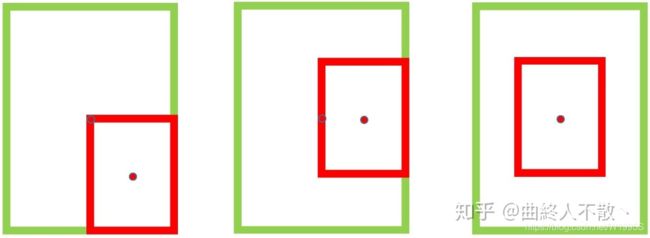第一种相比于第三种越不太可能是冗余框。基于该观点，研究者使用所提出的DIoU替代IoU作为NMS的评判准则，公式如下：
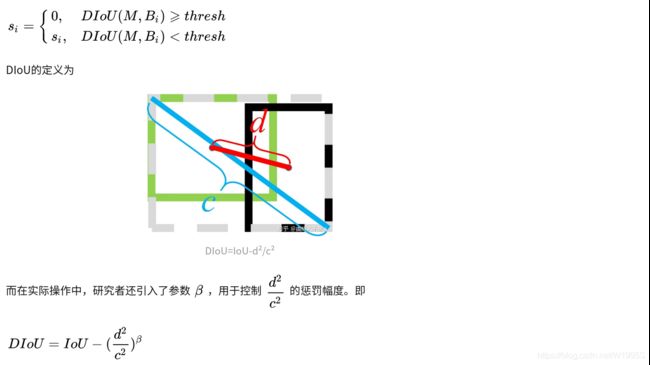由公式可以看出，