【cs231n Lesson3】Linear classifier, Loss function
个人学习笔记
date:2023.01.02
参考网址:CS231N官方笔记 线性分类
线性分类
KNN有几个缺点:
- 分类器需要存储训练集,以便于和测试图像比对。有时候训练集会达到gigabytes百亿字节。
- 花费时间高,需要将测试图像和每一张训练图像比对。我们需要训练成本高而不是测试成本高,应用可行性。
线性分类主要包含如下要素:
- score function F ( x i ; W ) F(x_{i};W) F(xi;W):原像素和分类之间的关系
- loss function L ( x i , y i ) L(x_{i},y_{i}) L(xi,yi):反映预测结果和实际结果之间的不可接受程度
linear classifier
(一) score function
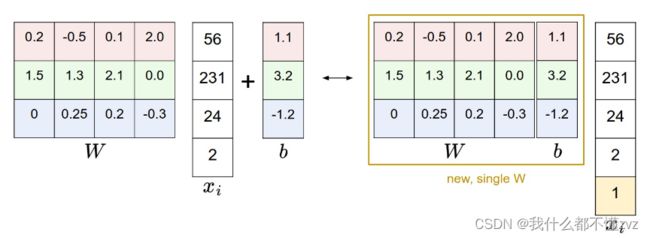
f ( x i , W , b ) = W x i + b f(x_{i},W,b) = Wx_{i}+b f(xi,W,b)=Wxi+b
如上等式,已假设输入图像 x i \bold x_{i} xi展开为shape为[D,1]的列向量,权重矩阵 W \bold W W是一个shape为[C,D]的矩阵,C表示分类数。得到一个[C,1]的列向量,表示各类的一个得分情况。 b \bold b b为bias偏重项,是一个[C,1]的列向量。
该方法的优点(相较于KNN):
- 一旦训练完成,我们需要的是学习到的参数(比如权重矩阵、bias vector、learning rate等)而不是训练集。
- 计算测试图像的得分只需要进行简单的矩阵运算,而不需要与每一张训练图像比对,速度更快也更高效。
- 将输入image展开成
[4,1]的列向量 - 权重矩阵为
[3,4],其中3表示3个分类,4表示每个分类下的4个pixels有不同的权重。既每一行都是一个类别的权重分类器。 - 权重矩阵和输入列向量进行点乘,得到一个
[3,1]列向量,表示每个分类的得分,再加上偏正项就是最终得分。
因为 f ( x i ; W ; b ) \bold f(x_{i};W;b) f(xi;W;b)是一个线性函数,如果将其可视化,就是如下图所示。
如果W被改变,那么直线会发生旋转
如果没有偏正项,那么 x i = 0 \bold x_{i}=0 xi=0的时候就永远在原点处。

如果将最终得到的权重矩阵每一行又转换为image尺寸,则会得到如下图形。
所以可以认为,线性分类实质上是模板匹配(template matching),我们训练最终就是得到一个模板,因此局限性非常大,同一类别下的实物只要有些许差异也许就不能被识别。且如上图所示,我们是用一条直线在二维平面上进行分类,因此局限性也很大(很多情况仅用直线是分类不了的)
Loss Function
一般形式
L ( x , y ) = 1 N ∑ i = 1 N L i ( f ( x i ; W ) , y i ) L(x,y) = \frac{1}{N}\sum_{i=1}^{N}L_{i}(f(x_{i};W),y_{i}) L(x,y)=N1i=1∑NLi(f(xi;W),yi)
Multicalss Support Vector Machine Loss( SVM Loss)
SVM loss 目的是想让正确类别的得分远远高于错误类别的得分,至少要高过某一个安全边距(fixed margin Δ Δ Δ)。当正确类别得分远高于错误类别得分时,损失值会很小。
公式:
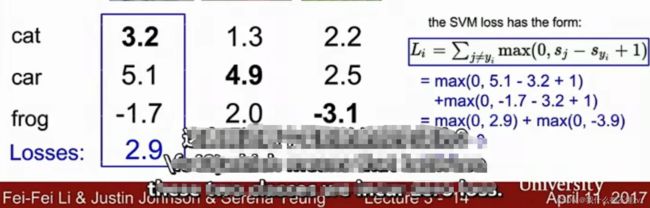
L i = ∑ j ≠ y i m a x ( 0 , s j − s y i + Δ ) L_{i} = \sum_{j\not =y_{i}} max(0,s_{j}-s_{y_{i}}+\Delta ) Li=j=yi∑max(0,sj−syi+Δ)
s j s_{j} sj为其他分类得分, s y i s_{y_{i}} syi为第i个样本得分, Δ \Delta Δ为自己设定的边距。
如果 s y i > s j + △ s_{y_{i}}>s_{j}+\triangle syi>sj+△ ,既样本得分远大于其他分类得分,那么取损失为0; 否则取损失为 s j − s y i + Δ s_{j}-s_{y_{i}}+\Delta sj−syi+Δ
- 如果正确类别得分比其他类别得分至少大于 Δ \Delta Δ或以上,那么损失值即为0。
- 如果损失值为0,那么正确类别得分有稍微变化,也不会影响损失值。
- 如果正确类别得分小于其他类别得分,或大于其他类别得分但不超过 Δ \Delta Δ,那么损失值不为0。因为SVM希望的是正确类别得分至少要大于其他类别得分超过 Δ \Delta Δ
上述损失函数又叫Hinge Loss SVM,由下图可见,该损失函数理论上最小值为0,最大值为 ∞ \infty ∞。
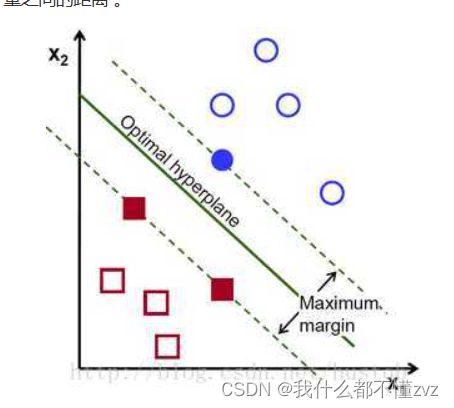
初次训练时,一般以趋于均值的权重矩阵开始,因此得到的分数都接近0,此时损失值应为 L o s s = C − 1 Loss = C - 1 Loss=C−1 (C为分类数,由公式可得,可用来验证)
如果有权重矩阵W使得损失值为0,W不是唯一的, λ W ( λ > 1 ) \lambda W(\lambda>1) λW(λ>1)也可能使损失值为0.
python实现(不包含正则项)
def L_i_vectorized(x, y, W):
"""
A faster half-vectorized implementation. half-vectorized
refers to the fact that for a single example the implementation contains
no for loops, but there is still one loop over the examples (outside this function)
"""
delta = 1.0
scores = W.dot(x)
# compute the margins for all classes in one vector operation
margins = np.maximum(0, scores - scores[y] + delta)
# on y-th position scores[y] - scores[y] canceled and gave delta. We want
# to ignore the y-th position and only consider margin on max wrong class
margins[y] = 0
loss_i = np.sum(margins)
return loss_i
L2-SVM Loss Function
L i = ∑ j ≠ y i m a x ( 0 , s j − s y i + Δ ) 2 L_{i} = \sum_{j\not =y_{i}} max(0,s_{j}-s_{y_{i}}+\Delta )^2 Li=j=yi∑max(0,sj−syi+Δ)2
损失函数用来权衡我们对预测值的不满意度,若使用平方项,则表示更坏的结果将接受更严重的惩罚。
Regularization正则化
分类器在训练集上表现如何不重要,在测试集上表现如何才重要。如果在训练集上表现得完美,那么可能导致过拟合现象。
当score function是高阶多项式时且完美拟合训练集,此时损失值为0,那么将会有很多个权重矩阵使得损失值也为0(上面提到)
ps. 如果W对应的损失值为15,那么2W对应的损失值为30.
所以假如正则项去对权重矩阵进行惩罚,越高阶惩罚力度越大。
正则项的目的是鼓励模型更简约(Occam’s Razor)
加入正则项损失后的损失函数
L ( x , y ) = 1 N ∑ i = 1 N L i ( f ( x i ; W ) , y i ) + λ R ( w ) L(x,y) = \frac{1}{N}\sum_{i=1}^{N}L_{i}(f(x_{i};W),y_{i})+\lambda R(w) L(x,y)=N1i=1∑NLi(f(xi;W),yi)+λR(w)
(一) L 2 正则项 {\color{Purple}L2正则项} L2正则项
R ( W ) = ∑ k ∑ l W k , l 2 R(W) = \sum_{k} \sum_{l} W_{k,l}^2 R(W)=k∑l∑Wk,l2
(二) L 1 正则项 {\color{Purple}L1正则项} L1正则项
R ( W ) = ∑ k ∑ l ∣ W k , l ∣ R(W) = \sum_{k} \sum_{l} |W_{k,l}| R(W)=k∑l∑∣Wk,l∣
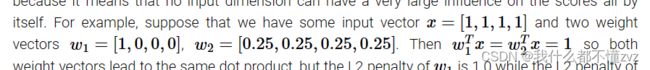
假如有如上数据,data loss都一样。
根据L2正则项, R ( w 2 ) = 0.5 R(w2) = 0.5 R(w2)=0.5而 R ( w 1 ) = 1 R(w1)=1 R(w1)=1,因此选择w2权重矩阵更合适。
但对于L1正则项, R ( w 2 ) = 1 R(w2) = 1 R(w2)=1且 R ( w 1 ) = 1 R(w1)=1 R(w1)=1,此处为特例。
一般来说,L2正则项鼓励输入列向量中的每个pixel都能影响到得分结果(所以选择w2,这样每个元素都乘以0.25,从而影响得分);而L1正则项则鼓励多使用稀疏矩阵。
一般来说,我们通过损失函数来纠正权重矩阵,而不去纠正偏重项,因为偏重项对结果的影响微乎其微。
Softmax classifier
(一)一般形式 \color{purple}(一) 一般形式 (一)一般形式

其中交叉熵为如下形式:
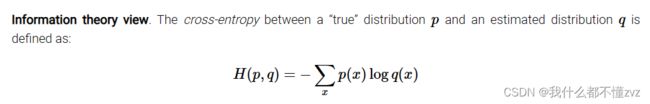
令 q ( x ) = e f y i ∑ j e f j , p ( x ) = 1 q(x)=\frac{e^{f_{y_{i}}}}{\sum_j e^{f_{j}}}, p(x)=1 q(x)=∑jefjefyi,p(x)=1
(二)交叉熵形式 \color{purple}(二) 交叉熵形式 (二)交叉熵形式
- score function: f ( x i ; W ) = W x i f(x_{i};W)=Wx_{i} f(xi;W)=Wxi
- 指数化、归一化
- 交叉熵(cross-entropy loss): L i = − l o g ( e f y i ∑ j e f j ) L_{i} = - log(\frac{e^{f_{y_{i}}}}{\sum_j e^{f_{j}}}) Li=−log(∑jefjefyi)
讨论:
- 需要归一化的原因是 ,指数化后结果可能非常大。
- 需要负号的原因是,损失函数表征我们对预测结果的不满意度,所以加一个负号。
- 理论上,最大值为无穷,最小值为0
- 初始化时,损失值应为 − l o g ( 1 c ) 或 l o g ( c ) - log(\frac{1}{c}) 或 log(c) −log(c1)或log(c)
- SVM loss,当损失值为0时,稍微改变正确结果得分并不会影响损值。但交叉熵损失不一样,让正确结果得分更高,则是其归一化更接近于1,损失更接近于0。
- softmax classifier的目的就是让正确结果得分更高,更高。
代码演示(错误演示和正确演示)
f = np.array([123, 456, 789]) # example with 3 classes and each having large scores
p = np.exp(f) / np.sum(np.exp(f)) # Bad: Numeric problem, potential blowup
# instead: first shift the values of f so that the highest number is 0:
f -= np.max(f) # f becomes [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # safe to do, gives the correct answer
SVM vs Softmax
- SVM 将得分视作分类得分,其目的是让正确结果至少比错误结果的得分大margin值
- Softmax 将得分视作 log 概率,并鼓励正确结果概率更大(与此同时错误结果概率更小)
- 损失函数值只有在同数据和同损失函数下才有对比的意义。
- SVM中,得分的意义是不容易解释的,只知道很可能是这个类,但得分本身的意义很难解释。
- Softmax中,得分被视作“概率”,又或者说置信度confidence。加上引号是因为该值与正则项的 λ \lambda λ有关。 λ \lambda λ越大,“概率”越趋于平均。所以此“概率”被认为是置信度更佳。
- 数字的排序是可解释的(哪个更有可能是预测的结果),但数字本身的意义和差别是难以解释的。
- SVM和Softmax关注的目标不同,前面已经提到过多次。SVM一旦满足就不管了,Softmax永不满足。
- SVM可以被视作是一种特征,例如有一个汽车分类器,我们应该把重心放在区分汽车和拖拉机,而不是区分汽车和青蛙(which assigns very low scores),这时候SVM就比Softmax好
小结
- 定义了score function(线性score函数,取决于权重矩阵和偏重项bias)
- 相比于KNN,不占用空间,测试速度更快
- 定义了损失函数(SVM和Softmax),并比较了两者。
- 学习了正则项(L1、L2)