Bert基础解读(一)—— transformer之attention机制(self-attention)看不明白你打我
transformer是一种seq2seq模型。那这种模型特殊之处在于什么呢?它的特殊之处就在于这个模型里面,大量的运用了self-attention这种类layer.
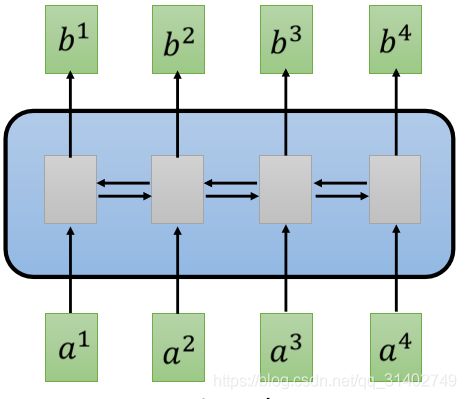
如果我们一般讲到要处理一个sequence,我们最常想到的一种方法,就是用RNN架构。RNN的输入就是一串vector sequence。他的输出就是另外一串vector sequence。
那如果我们是单向的RNN,到我们输出这个b4的时候,我们会把a1—a4通通都看过了。那如果我们输出b3的时候,我们把a1—a3都看过了。但是如果我们是双向rnn的话,那当我们输出上边的每一个b1到b4的时候,我们这个时候要把整个输入序列都看过,才能输出b1到b4。
RNN就非常适用在输入是一个sequence这种情况。但是他有一个问题,就是RNN不容易被平行化。怎么说它不容易被平行化呢?因为假设你今天要算出b4,在单向的情况下,你要先看a1,再看a2,再看a3,再看a4,这样的我们才能输出b4。这种就是不平行的,所以怎么办呢?
接下来就是提出了把CNN拿来取rnn的情况,现在输入仍然是一个序列,但我们不用RNN来处理它,而用CNN来处理它.
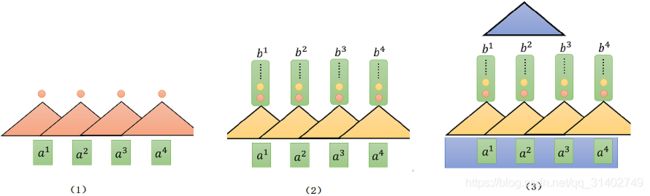
现在这样,每一个三角形都代表一个filter(卷积核),那现在的输入就变成了序列中的其中一小段,比如说上图(1)中这个红色的filter,他就是三个向量作为输入,然后输出一个数值。这个filter就把这三个向量里面的内容做内积,输出一个红色的点,这个红色的点就代表内积之后的结果。这样filter不止只有一个,有红色的卷积核,黄色的卷积核(图(2)所示),当然,黄色的卷积核产生另外一排不同的数值。所以用CNN确实也可以做到rnn一样的输出输出形式差不多。
但是现在问题是:这边的每一个CNN,它只能够考虑非常有限的内容。这边每一个CNN,他只考虑了三个向量,不像这边的RNN,他可以考虑整个句子,然后再考虑输出。但是CNN也不是没有办法考虑更长的信息的,如图(3)所示,你只要叠很多层CNN,上层的filter,就可以考虑比较多的信息。举例来说,我们先叠了第一层的CNN之后,再叠第二层的CNN,第二层的filter会把第一层的输出当作他的输入,这个蓝色的filter就会看b1、b2、b3,来决定它的输出,而b1、b2、b3是根据a1到a4来决定他们的输出的,所以等同于这个蓝色的filter,其实已经看了a1到a4整个句子里面所有的内容。所以如果cnn叠很多层,他其实也可以看很长时间的资讯。而CNN的好处就是它是可以平行化的,上面的每一个filter在做计算的时候都是可以一起的,你不需要等到第一个filter算完之后再算第二个filter,你可以全部的filter一起计算,你也不需要等红色的filter算完再算黄色的,他们这都可以同时计算。
但是他也有一个缺点,就是它一定要叠很多层,才能把整个句子的系列都看完,那如果我们第一层的filter就想得到更长的资讯,那这个我们做不到,因为它只能够看很小的范围 。所以怎么办?
有一个更好的解决方案,叫self-attention. 这个层的作用就是取代rnn原来可以做的事情。就我们接下来讲的东西就是一个事情,就是我们有一个新的layer,叫做self-attention layer,这个layer可以取代rnn layer,他们的输入和输出都是一样的,输入一个sequence,输出一个sequence。self-attention layer特别的地方是,他跟双向的rnn有同样的能力,双向的rnn每一个输出都看过整个句子,而self-attention layer每输出一个值,他也看过了整个句子,但是神奇的地方是。b1—b4,他们是同时计算的,他们可以同时被算出来,不需要先算完b1,然后再算b2,然后再算b3b4。就所有论文里能rnn做的事情,你都可以用selfattention做。
self-attention的概念最早出现在一篇叫attention is all you need论文。那这个东西是怎么做的呢?
1.self-attention
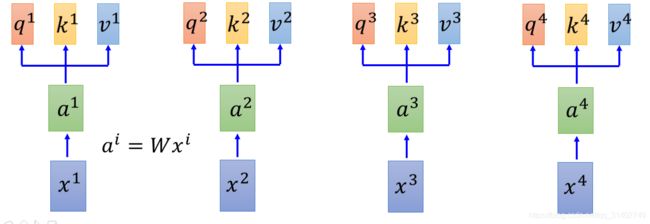
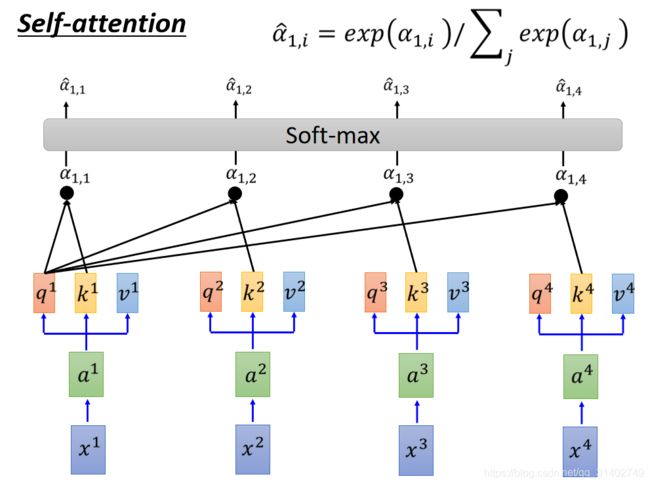
首先我们的输入是x1到x4这个sequence,可以是一个句子。我们为每一个input a1,a2,a3,a4 乘以一个矩阵,得到每个输入的embeding :a1—a4。然后我们把a1到a4丢进self-attention layer. 那self-attention layer里面是做什么呢?在self-attention layer里面,每一个输入,都分别乘上三个不同的矩阵,产生三个不同的向量。那这三个不同的向量,我们分别把它命名为q k v。
q代query,是要去match其他人的。每一个输入向量a都乘上某一个矩阵![]() 得到q1、q2、q3、q4。这些东西叫做query。接下来用同样的方法,但是把a乘上不同的矩阵
得到q1、q2、q3、q4。这些东西叫做query。接下来用同样的方法,但是把a乘上不同的矩阵![]()
![]() ,得到k1、k2、k3、k4,这些k叫做key,是拿来被query match,等一下我们会看到k是怎么用的。然后这个v呢,叫做value,v是被抽取出来的信息,是由a乘上不同的矩阵
,得到k1、k2、k3、k4,这些k叫做key,是拿来被query match,等一下我们会看到k是怎么用的。然后这个v呢,叫做value,v是被抽取出来的信息,是由a乘上不同的矩阵![]()
![]() 得到的。
得到的。
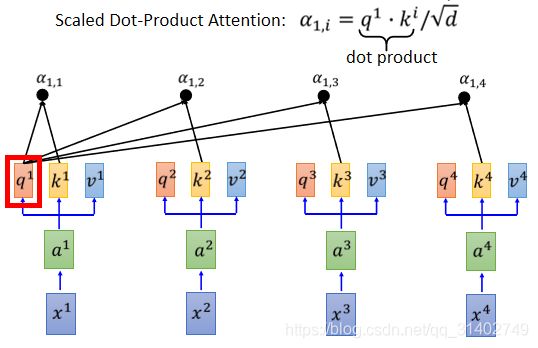
现在,我们的每一个输入,也就是每一个a都有q k v三个不同的向量。接下来,我们要做的事情是什么呢?我们要做的事情就是,拿每一个不同的query q去对每一个不同的key k 做attention这件事情。我们先把q1拿出来,(等一下每一个q都要被用到,我们先把q1拿出来),我们把q1对k1做attention。attention的本质就是输入两个向量,输出就是这两个向量有多匹配,总之就是输入两个向量,输入一个分数,表示这两个向量有多匹配。(attention的式子可以采用很多不同的方法,这里我们采取图片中的式子,先内积再除根号d。d是k和v的维度,因为k和v可以做内积,因此k和v的维度是一样的。至于为什么除以根号d,论文中有证明,这里不再细说。为什么要内积呢?因为我们做attention的目的就是衡量两个向量的相似度,而内积的几何意义就是:两个向量越相似,则两个向量的内积越大)。把q1对k1做attention,得到一个数值,代表q1与k1attention的权重,叫![]() ,代表q1对k1的attention。接下来,我们拿q1跟k2做attention得到
,代表q1对k1的attention。接下来,我们拿q1跟k2做attention得到![]() ,拿q1跟k3做attention得到
,拿q1跟k3做attention得到![]() ,拿q1跟k4做attention得到
,拿q1跟k4做attention得到![]() 。
。
那这个α怎么算呢?在论文里面用的方法叫做scaled dot-product,也就是说,这下面的![]() 是怎么来的呢?就是拿
是怎么来的呢?就是拿![]() 对
对![]() 做内积,然后再除以根号d。比较难理解的是为什么除以根号d。那d是什么呢?d是q和k的维度,因为这里q和v做内积,所以q跟v的维度是一样的,我们把塔表示为d。那这里为什么要除以根号d呢?一个直观的解释是说:q跟k做内积的数值,会随着维度的增大方差就会变大。这个很直观:随着q跟k维度的增大,他们做内积时相加的元素就越多,所以方差就越大,所以我们除以d来平衡这件事情,那为什么是除以根号d而不是其他的东西呢?因为论文就是这么写的…
做内积,然后再除以根号d。比较难理解的是为什么除以根号d。那d是什么呢?d是q和k的维度,因为这里q和v做内积,所以q跟v的维度是一样的,我们把塔表示为d。那这里为什么要除以根号d呢?一个直观的解释是说:q跟k做内积的数值,会随着维度的增大方差就会变大。这个很直观:随着q跟k维度的增大,他们做内积时相加的元素就越多,所以方差就越大,所以我们除以d来平衡这件事情,那为什么是除以根号d而不是其他的东西呢?因为论文就是这么写的…
接下来,我们做softmax,也就是我们把![]() 到
到![]() 经过一个softmax layer得到
经过一个softmax layer得到![]() 到
到![]() 。
。
做完softmax以后,我们拿![]() 去跟每一个
去跟每一个![]() 相乘:我们把
相乘:我们把![]() 乘以
乘以![]() ,把
,把![]() 乘以
乘以![]() ,把
,把![]() 乘以
乘以![]() ,把
,把![]() 乘以
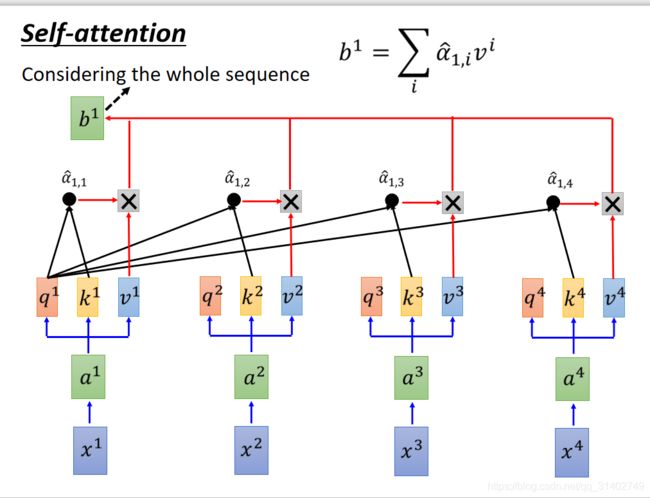
乘以![]() ,再把找得到的结果加来,就得到一个向量,该向量就是输出序列的第一个向量b1。如下图所示:
,再把找得到的结果加来,就得到一个向量,该向量就是输出序列的第一个向量b1。如下图所示:
我们说selt-attention就是输入一个sequence,输出一个sequence,现在我们得到输入sequence的第一个向量b1了。但是,你会发现我们再产生b1的时候,用了整个输入sequence的信息:b1是通过v1到v4做累加得到的,而v1-v4又是通过a1-a4通过矩阵变换得到的。所以等于是你产生b1的时候,你已经看到了整个句子的全局信息。那如果你产生b1的时候,不想考虑这么多的信息,你只想考虑局部信息,对attention-layer来说,也是做的到的。它只要让后边的α产生出来的值变成零,他就考虑的局部的信息。如果他想考虑远一点的信息,如a4,只要让α4有值即可。对于b1来说,就有一种天涯若比邻的感觉。对b1来说,不管是近代东西还是远的东西,只要他想,他就可以用attention去把他看到,至于要看近还是要看远,要看输入序列的哪一个部分,就是attention自己用学的方式来决定他。 那刚刚我们算出的是b1,其实在同一时间,我们也可以算b2、b3、b4。
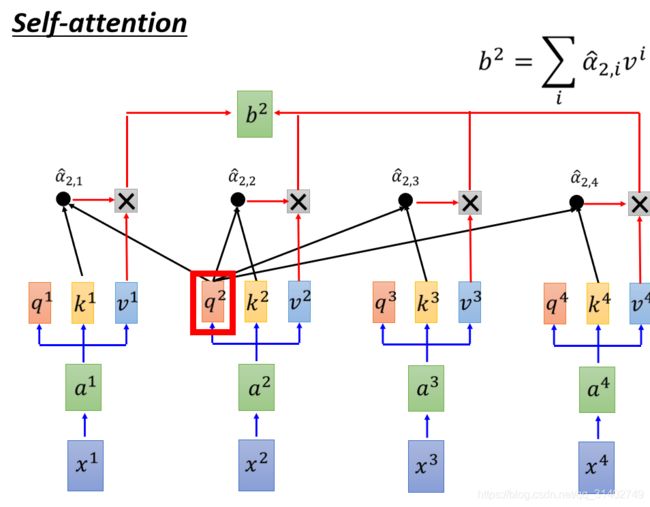
下图展示一下b2的计算过程:
大体来说,输入序列a1 a2 a3 a4,得到输出序列b1 b2 b3 b4。 该过程和rnn是一样的,只是attention-layer可以使得b1 b 2 b3 b4同时运算。
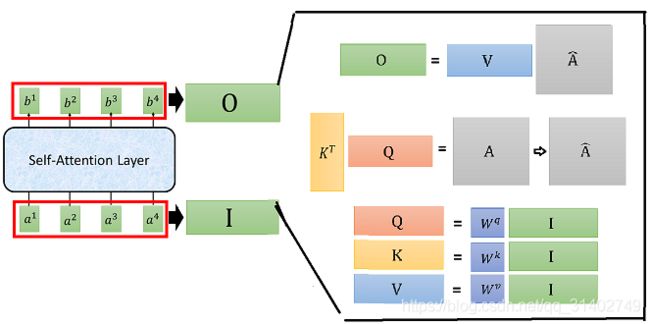
接下来我们把刚刚一连串的过程用矩阵表示。
- 首先,我们知道
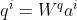 ,
, ,
,
 Wq乘以a1得到q1
Wq乘以a1得到q1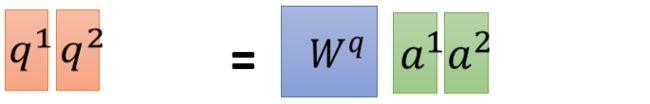 Wq乘以a2得到q2
Wq乘以a2得到q2 Wq乘以a3,a4分别得到q3,q4
Wq乘以a3,a4分别得到q3,q4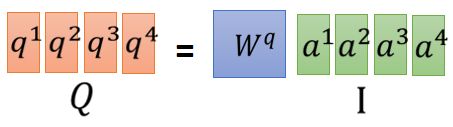 把a1 a2 a3 a4拼起来变成一个矩阵,用I表示,我们用Wq*I 就可以得到Q,Q里面的第i列,就代表
把a1 a2 a3 a4拼起来变成一个矩阵,用I表示,我们用Wq*I 就可以得到Q,Q里面的第i列,就代表
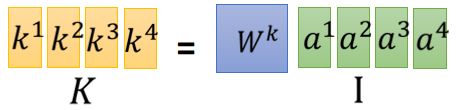
 同理,我们可以得到:K = Wq*I 、V = Wq*I
同理,我们可以得到:K = Wq*I 、V = Wq*I 、
、 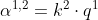 、
、 、
、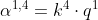
- 为了简便计算,我们先忽视根号d
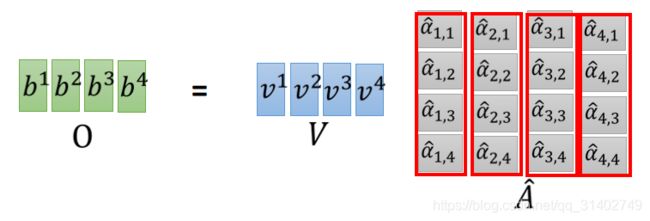
b1 = v1*a11+v2*a12+v3*a13+v4*a14,同理算出b2,b3,b4,b1—b4构成输出矩阵O
我们再把刚刚的过程简化以下:
2.muti-head-self-attention
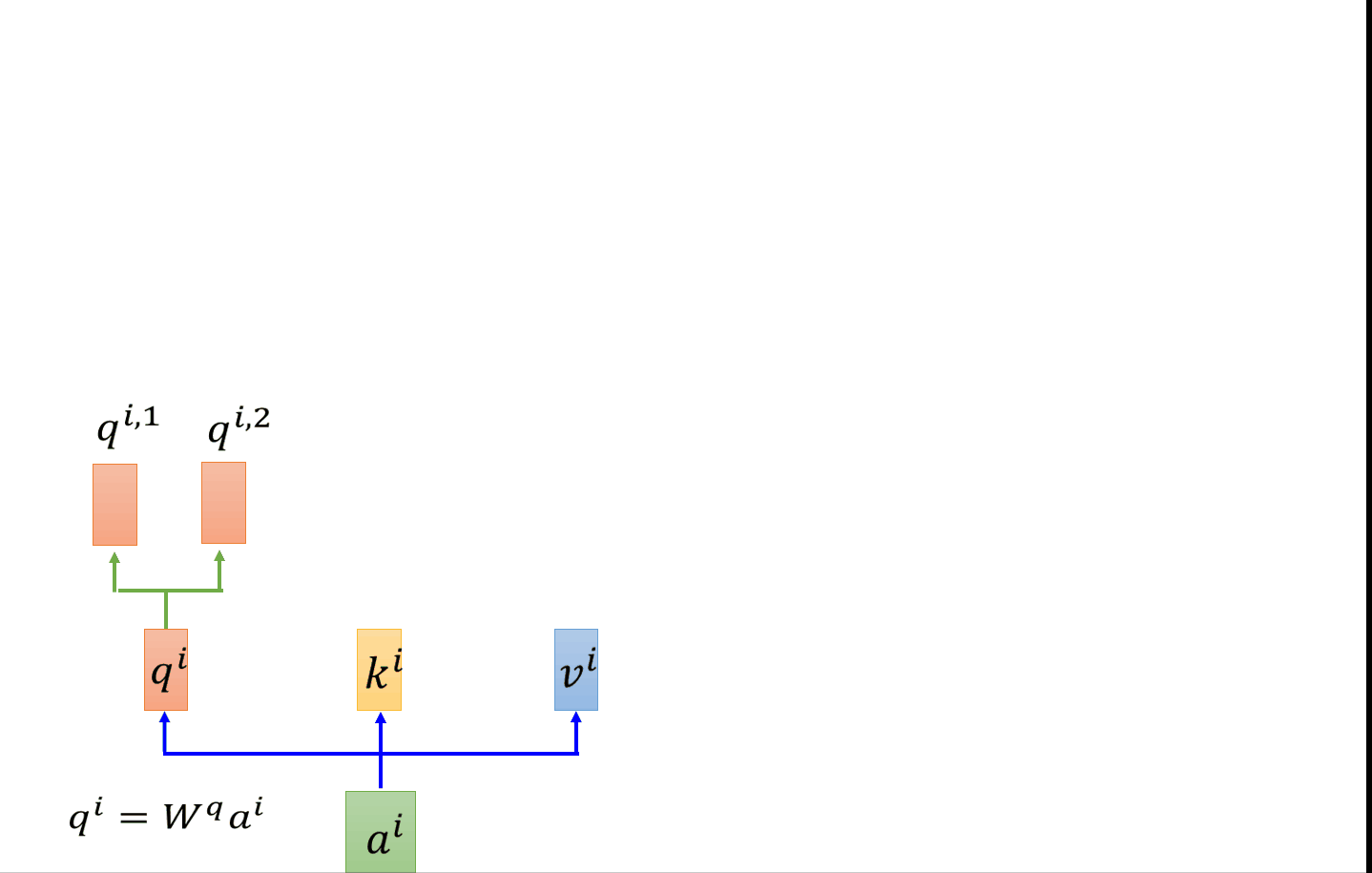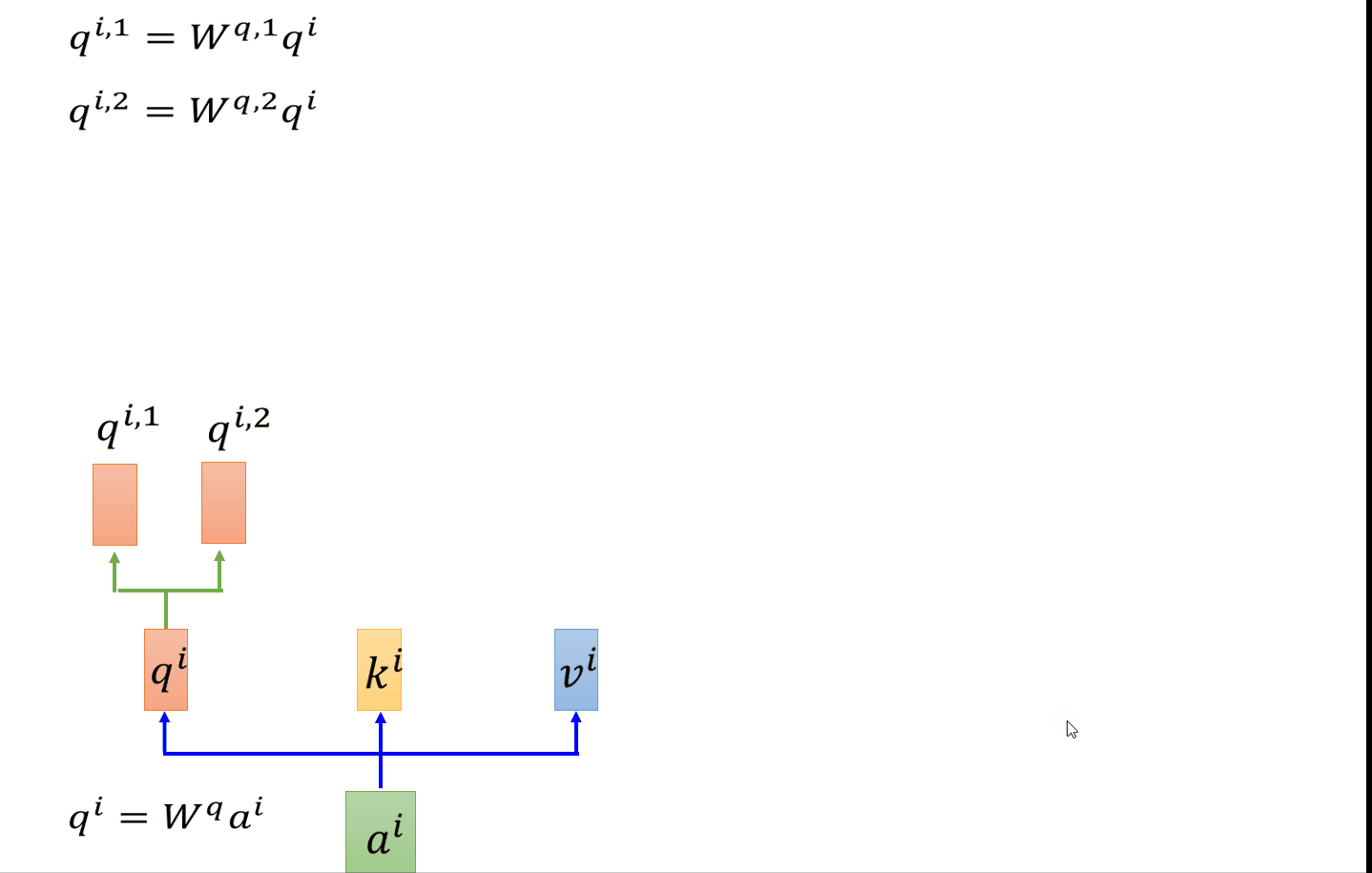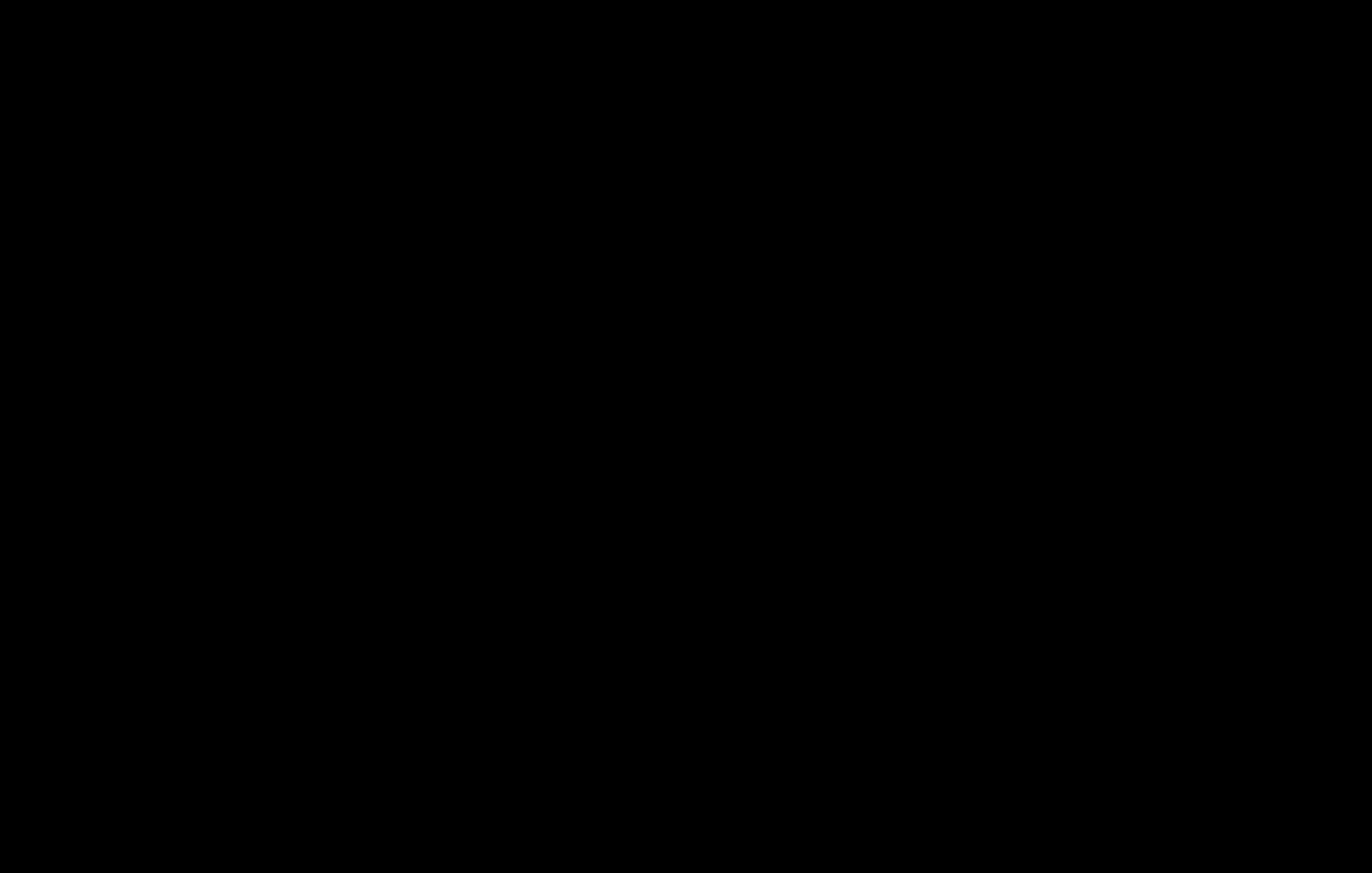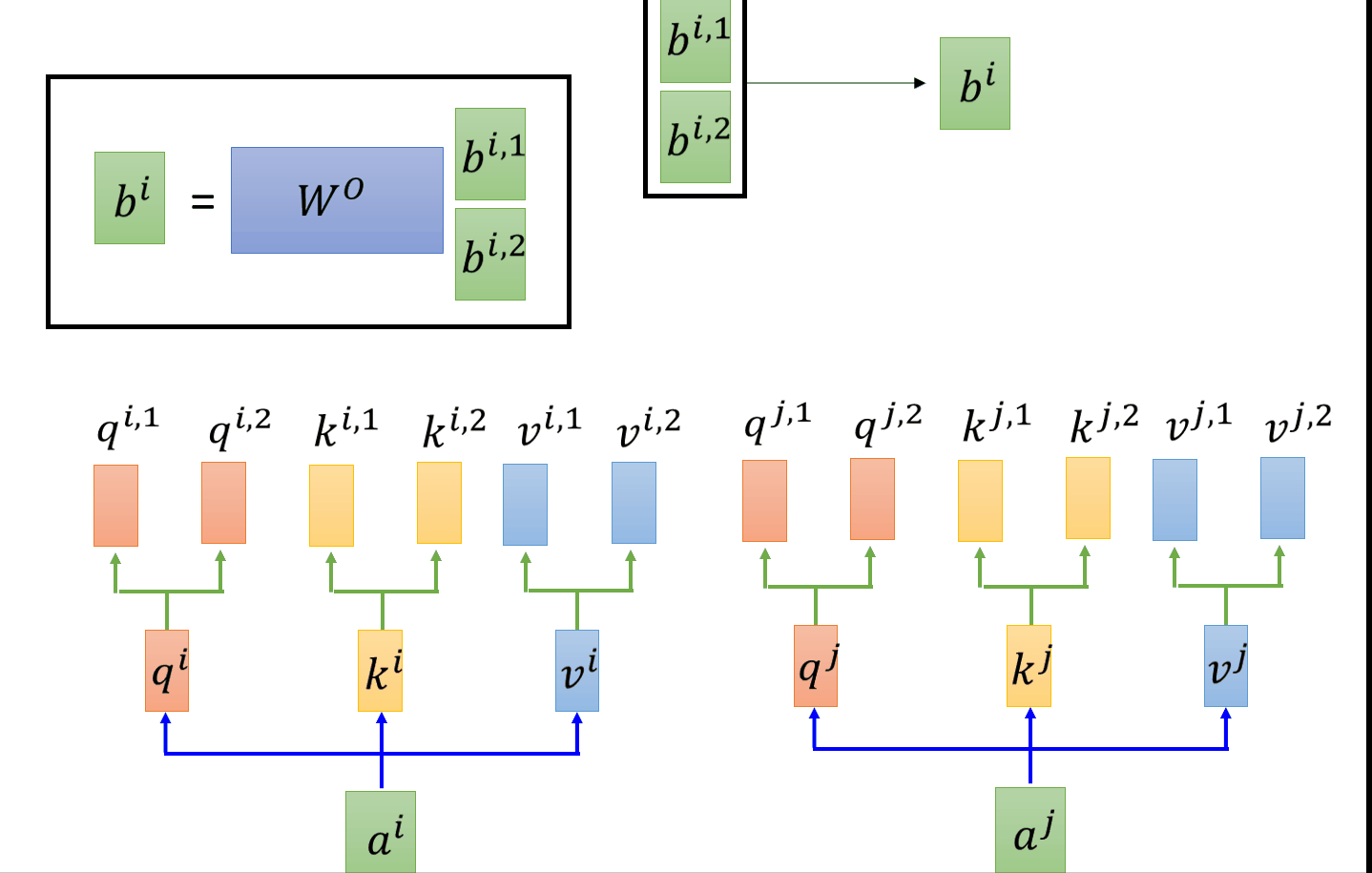
以head=2为例 ,在self-attention中,每一个ai都会得到一个qi,ki,vi。在有两个head的前提下,会把每个qkv分裂,变成两个。以q为例,做法可以是把qi乘上两个不同的矩阵,得到qi1和qi2。接下来做跟刚才一样的self-attention。只是qi1只会对跟他同样是第一个的k做attention(看图就能明白)。q和k相乘得attention之后,与各自的v相乘、累加。得到bi1,bi2。然后我们把bi1和bi2 concat起来,然后把他乘以一个矩阵进行降维得到bi。设置多个head的好处就是,不同的head关注的点是不同的,举个例子,有的head关注局部信息,而有的head关注全局信息,当你有muti-head的之后,每个head的关注的点不一样,他们各司其职。
3.positional encoding
由于transformer模型没有循环神经网络的迭代操作, 才能识别出语言中的顺序关系。但是如果我们仔细回顾一下刚才的两个过程就会发现,对于self-attenton来说,我们输入的序列的顺序是不重要的,因为对于input来说,只需要跟每个人都做self-attention,所以对于每个input的来说,无论其他input的距离是近还是远,对他来说,作用都是一样的。但是我们希望把input的顺序考虑到self-attention里面,所以我们必须提供每个字的位置信息给self-attention,原始的论文里采用positional encoding方法。
当原始输入xi经过embedding得到ai之后,需要再加上一个和ai的维度相等的ei,ei是人手设的,ei表示ai的位置。接下来就跟前面两个过程一样。