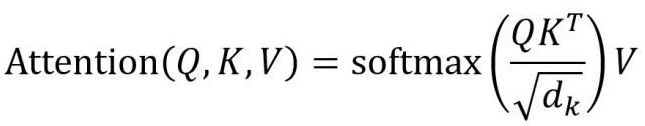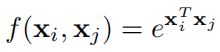cv中的注意力机制

self-attention理解：

先从下面这个公式去看：

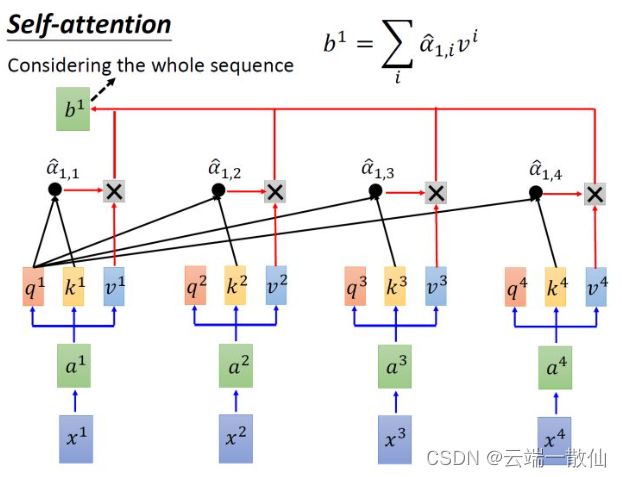
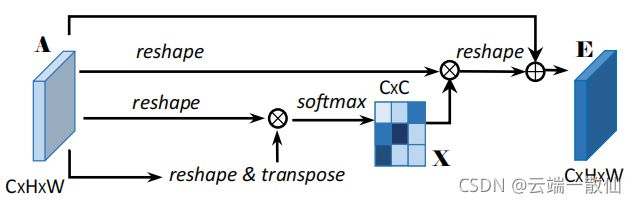
矩阵可以看作由一些向量组成，一个矩阵乘以它自己转置的运算，等同于向量分别与其他向量计算内积，（内积则表示为：两个向量的夹角，一个向量在另一个向量上的投影），投影的值大，说明两个向量相关度高；Softmax的意义为归一化，给矩阵中每个数一个权重值；最后再与X矩阵相乘，最后的结果就是加权求和之后的表示。

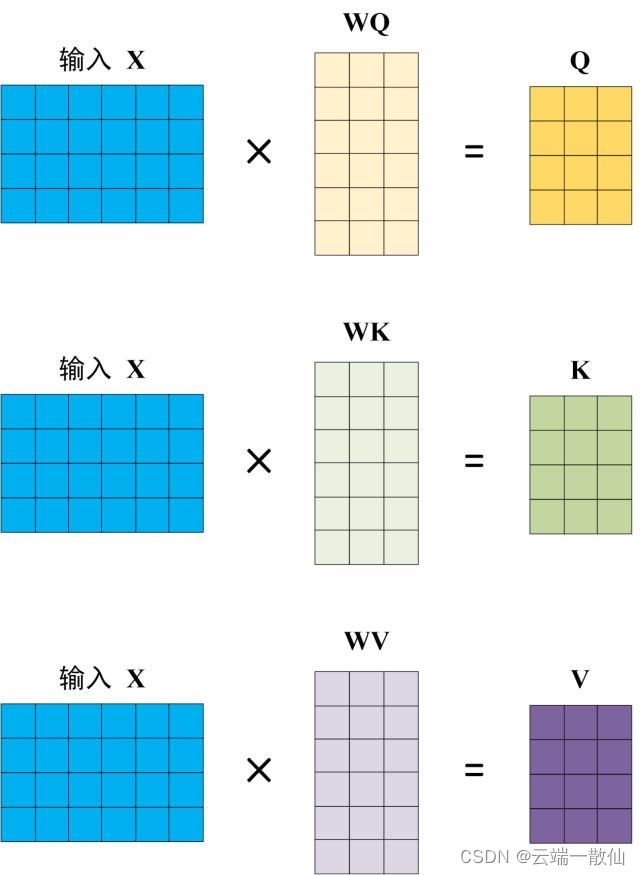
$Q，K，V$的计算都与输入X相关，为什么不直接使用而要对其进行线性变换？当然是为了提升模型的拟合能力，矩阵都是可以训练的，起到一个缓冲的效果。
假设$Q，K$里的元素的均值为0，方差为1，那么$Q{K}^T$中元素的均值为0，方差为d. 当d变得很大时， $Q{K}^T$中的元素的方差也会变得很大，如果$Q{K}^T$中的元素方差很大，那么$softmax(Q{K}^T)$的分布会趋于陡峭(分布的方差大，分布集中在绝对值大的区域)。总结一下就是$softmax(Q{K}^T)$的分布会和d有关。因此 $softmax(Q{K}^T)$中每一个元素除以$\sqrt[2]{d_k}$后，方差又变为1。这使得$softmax(Q{K}^T)$的分布“陡峭”程度与d解耦，从而使得训练过程中梯度值保持稳定。

注意力机制（attention）的基本思想就是想让系统学会注意力——能够忽略无关信息而关注重点信息，与机器翻译中的Attention应用思想类似，视觉中的Atttention其实也是学出一个权重分布，再拿这个权重分布施加在原来特征之上。不过施加权重的方式略有差别，视觉应用中一般有以下几种施加方式：

• 加权可以保留所有分量做加权(soft attention)；

• 可以在分布中以某种采样策略选取部分分量做加权(hard attention)

• 加权可以作用在原图上

• 加权可以作用在空间尺度上，给不同空间区域加权

• 加权可以作用在Channel尺度上，给不同通道特征加权

• 加权可以作用在不同时刻历史特征上，结合循环结构添加权重

single-head self-attention

multi-head self-attention

SENet

作用在Channel尺度上，给不同通道特征加权，学习了channel之间的相关性，筛选出了针对通道的注意力


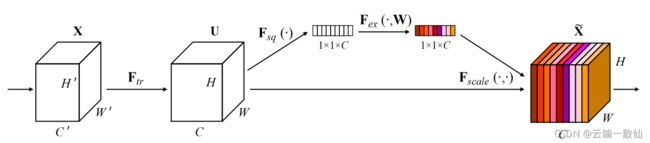
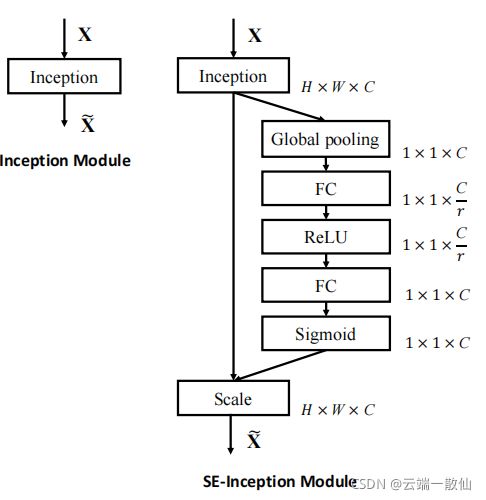
Squeeze操作（对应SE block结构图中的Fsq操作），就是一个global average pooling，使其具有全局的感受野，使得网络低层也能利用全局信息

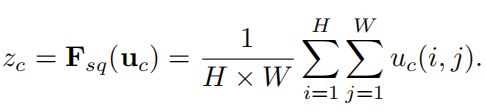
Excitation操作全面捕获通道依赖性（相互之间的重要性），前面的squeeze都只是在某个channel的feature map里面操作，这两个全连接层的作用就是融合各通道的feature map信息

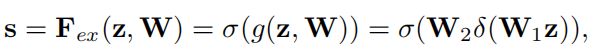
Fscale操作就是channel-wise multiplication，Uc表示U中第c个二维矩阵，下标c表示channel。Uc是一个二维矩阵，Sc是上一步的输出S(向量)中的一个数值，也就是权重，因此相当于把Uc矩阵中的每个值都乘以Sc

代码：

class SELayer(nn.Module):
    def __init__(self, channel, reduction=16):
        super(SELayer, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.fc = nn.Sequential(
            nn.Linear(channel, channel // reduction, bias=False),
            nn.ReLU(inplace=True),
            nn.Linear(channel // reduction, channel, bias=False),
            nn.Sigmoid()
        )

    def forward(self, x):
        b, c, _, _ = x.size()
        y = self.avg_pool(x).view(b, c)
        y = self.fc(y).view(b, c, 1, 1)
        return x * y.expand_as(x)

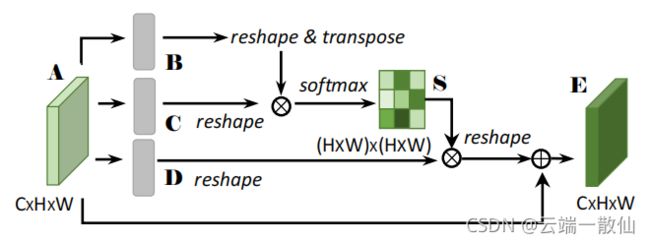
Non-local Neural Networks

Non-local属于self-attention的一种，只涉及到了位置注意力模块，而没有涉及常用的通道注意力机制
通用公式：

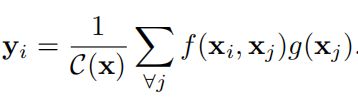
• x是输入信号，cv中使用的一般是feature map

• i 代表的是输出位置，如空间、时间或者时空的索引，响应应该对j进行枚举然后计算得到的

• f 函数计算i和j的相似度

• g 函数计算feature map在j位置的表示

• 最终的y是通过响应因子C(x) 进行标准化处理以后得到的
  
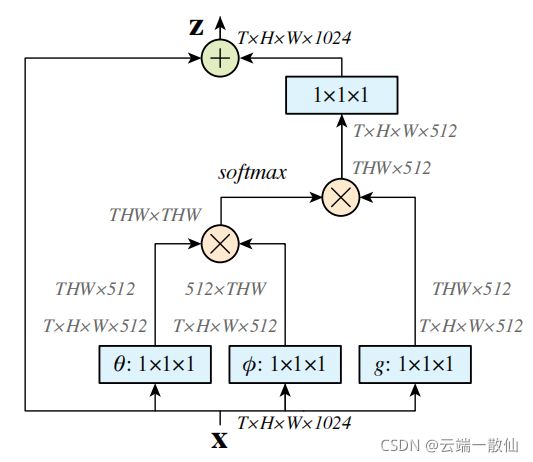
  f函数：用于计算i和j相似度的函数，作者提出了四个具体的函数可以用作f函数

• Gaussian

• Embedded Gaussian

• Dot product
  

• Concatenation
  

g函数：可以看做一个线性转化（Linear Embedding）

class _NonLocalBlockND(nn.Module):
    def __init__(self,
                 in_channels,
                 inter_channels=None,
                 dimension=3,
                 sub_sample=True,
                 bn_layer=True):
        super(_NonLocalBlockND, self).__init__()

        assert dimension in [1, 2, 3]

        self.dimension = dimension
        self.sub_sample = sub_sample

        self.in_channels = in_channels
        self.inter_channels = inter_channels

        if self.inter_channels is None:
            self.inter_channels = in_channels // 2
            # 进行压缩得到channel个数
            if self.inter_channels == 0:
                self.inter_channels = 1

        if dimension == 3:
            conv_nd = nn.Conv3d
            max_pool_layer = nn.MaxPool3d(kernel_size=(1, 2, 2))
            bn = nn.BatchNorm3d
        elif dimension == 2:
            conv_nd = nn.Conv2d
            max_pool_layer = nn.MaxPool2d(kernel_size=(2, 2))
            bn = nn.BatchNorm2d
        else:
            conv_nd = nn.Conv1d
            max_pool_layer = nn.MaxPool1d(kernel_size=(2))
            bn = nn.BatchNorm1d

        self.g = conv_nd(in_channels=self.in_channels,
                         out_channels=self.inter_channels,
                         kernel_size=1,
                         stride=1,
                         padding=0)

        if bn_layer:
            self.W = nn.Sequential(
                conv_nd(in_channels=self.inter_channels,
                        out_channels=self.in_channels,
                        kernel_size=1,
                        stride=1,
                        padding=0), bn(self.in_channels))
            nn.init.constant_(self.W[1].weight, 0)
            nn.init.constant_(self.W[1].bias, 0)
        else:
            self.W = conv_nd(in_channels=self.inter_channels,
                             out_channels=self.in_channels,
                             kernel_size=1,
                             stride=1,
                             padding=0)
            nn.init.constant_(self.W.weight, 0)
            nn.init.constant_(self.W.bias, 0)

        self.theta = conv_nd(in_channels=self.in_channels,
                             out_channels=self.inter_channels,
                             kernel_size=1,
                             stride=1,
                             padding=0)
        self.phi = conv_nd(in_channels=self.in_channels,
                           out_channels=self.inter_channels,
                           kernel_size=1,
                           stride=1,
                           padding=0)

        if sub_sample:
            self.g = nn.Sequential(self.g, max_pool_layer)
            self.phi = nn.Sequential(self.phi, max_pool_layer)

    def forward(self, x):
        '''
        :param x: (b, c,  h, w)
        :return:
        '''

        batch_size = x.size(0)

        g_x = self.g(x).view(batch_size, self.inter_channels, -1)#[bs, c, w*h]
        g_x = g_x.permute(0, 2, 1)

        theta_x = self.theta(x).view(batch_size, self.inter_channels, -1)
        theta_x = theta_x.permute(0, 2, 1)

        phi_x = self.phi(x).view(batch_size, self.inter_channels, -1)
        
        f = torch.matmul(theta_x, phi_x)

        print(f.shape)

        f_div_C = F.softmax(f, dim=-1)

        y = torch.matmul(f_div_C, g_x)
        y = y.permute(0, 2, 1).contiguous()
        y = y.view(batch_size, self.inter_channels, *x.size()[2:])
        W_y = self.W(y)
        z = W_y + x
        return z

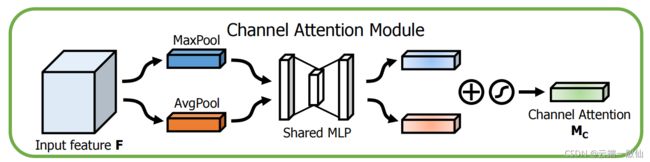
CBAM

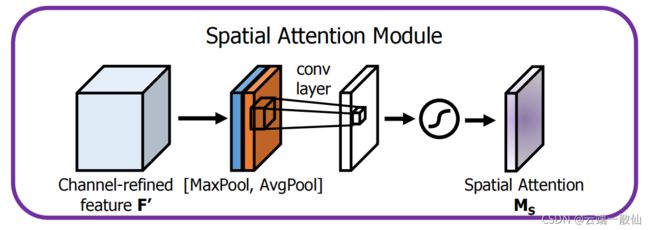
CBAM在channel和spatial两个维度上引入了attention机制，总体结构：

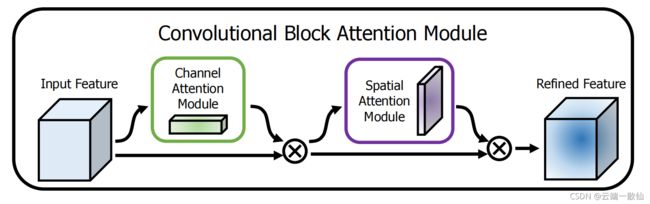
• 空间注意力模块

采用了全局平均池化和最大池化两种方式来分别利用不同的信息

• 通道注意力模块

与通道注意力相似，给定一个 H×W×C 的特征 F，我们先分别进行一个通道维度的平均池化和最大池化得到两个 H×W×1 的通道描述，并将这两个描述按照通道拼接在一起。然后，经过一个 7×7 的卷积层，激活函数为 Sigmoid，得到权重系数 Ms。最后，拿权重系数和特征 F’相乘即可得到缩放后的新特征

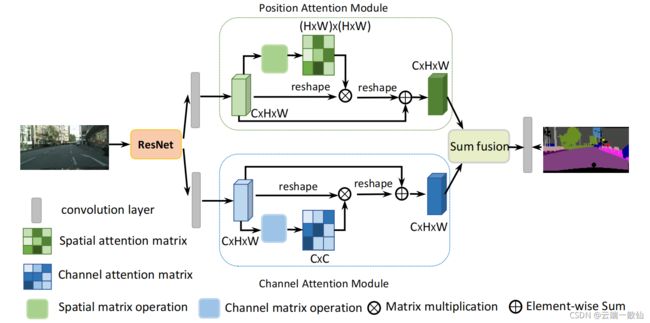
DANet

参考博客：
论文阅读笔记—senet
Non-local Neural Networks 原理详解及自注意力机制思考
视觉注意力机制 | Non-local 模块与 Self-attention 的之间的关系与区别？