Bandit算法原理及Python实战
目录
1)什么是Bandit算法
为选择而生。
Bandit算法与推荐系统
怎么选择Bandit算法?
2)常用Bandit算法
Thompson sampling算法
UCB算法
Epsilon-Greedy算法
Greedy算法
3)Bandit算法Python实战
参考资料:
推荐系统里面有两个经典问题:EE和冷启动。Bandit算法是一种简单的在线学习算法,常常用于尝试解决这两个问题,本文为你介绍基础的Bandit算法原理及Python实战。
1)什么是Bandit算法
为选择而生。
我们会遇到很多选择的场景。上哪个大学,学什么专业,去哪家公司,中午吃什么等等。这些事情,都让选择困难症的我们头很大。那么,有算法能够很好地对付这些问题吗?
当然有!那就是Bandit算法。
Bandit算法来源于历史悠久的赌博学,它要解决的问题是这样的:
一个赌徒,要去摇老虎机,走进赌场一看,一排老虎机,外表一模一样,但是每个老虎机吐钱的概率可不一样,他不知道每个老虎机吐钱的概率分布是什么,那么每次该选择哪个老虎机可以做到最大化收益呢?这就是多臂赌博机问题(Multi-armed bandit problem, K-armed bandit problem, MAB)。如下图所示:
![]()
怎么解决这个问题呢?最好的办法是去试一试,不是盲目地试,而是有策略地快速试一试,这些策略就是Bandit算法。
这个多臂问题,推荐系统里很多问题都与它类似:
- 假设一个用户对不同类别的内容感兴趣程度不同,那么我们的推荐系统初次见到这个用户时,怎么快速地知道他对每类内容的感兴趣程度?这就是推荐系统的冷启动。
- 假设我们有若干广告库存,怎么知道该给每个用户展示哪个广告,从而获得最大的点击收益?是每次都挑效果最好那个么?那么新广告如何才有出头之日?
- 我们的算法工程师又想出了新的模型,有没有比A/B test更快的方法知道它和旧模型相比谁更靠谱?
- 如果只是推荐已知的用户感兴趣的物品,如何才能科学地冒险给他推荐一些新鲜的物品?
Bandit算法与推荐系统
在推荐系统领域里,有两个比较经典的问题常被人提起,一个是EE问题,另一个是用户冷启动问题。
什么是EE问题?又叫exploit-explore问题。exploit就是:对用户比较确定的兴趣,当然要利用开采迎合,好比说已经挣到的钱,当然要花;explore就是:光对着用户已知的兴趣使用,用户很快会腻,所以要不断探索用户新的兴趣才行,这就好比虽然有一点钱可以花了,但是还得继续搬砖挣钱,不然花完了就得喝西北风。
用户冷启动问题,也就是面对新用户时,如何能够通过若干次实验,猜出用户的大致兴趣。
我想,屏幕前的你已经想到了,推荐系统冷启动可以用Bandit算法来解决一部分。
这两个问题本质上都是如何选择用户感兴趣的主题进行推荐,比较符合Bandit算法背后的MAB问题。
比如,用Bandit算法解决冷启动的大致思路如下:用分类或者Topic来表示每个用户兴趣,也就是MAB问题中的臂(Arm),我们可以通过几次试验,来刻画出新用户心目中对每个Topic的感兴趣概率。这里,如果用户对某个Topic感兴趣(提供了显式反馈或隐式反馈),就表示我们得到了收益,如果推给了它不感兴趣的Topic,推荐系统就表示很遗憾(regret)了。如此经历“选择-观察-更新-选择”的循环,理论上是越来越逼近用户真正感兴趣的Topic的,
怎么选择Bandit算法?
现在来介绍一下Bandit算法怎么解决这类问题的。Bandit算法需要量化一个核心问题:错误的选择到底有多大的遗憾?能不能遗憾少一些?
王家卫在《一代宗师》里寄出一句台词:
人生要是无憾,那多无趣?
而我说:算法要是无憾,那应该是过拟合了。
所以说:怎么衡量不同Bandit算法在解决多臂问题上的效果?首先介绍一个概念,叫做累积遗憾(regret):
![]()
图2 积累遗憾
这个公式就是计算Bandit算法的累积遗憾,解释一下:
首先,这里我们讨论的每个臂的收益非0即1,也就是伯努利收益。
然后,每次选择后,计算和最佳的选择差了多少,然后把差距累加起来就是总的遗憾。
wB(i)是第i次试验时被选中臂的期望收益, w*是所有臂中的最佳那个,如果上帝提前告诉你,我们当然每次试验都选它,问题是上帝不告诉你,所以就有了Bandit算法,我们就有了这篇文章。
这个公式可以用来对比不同Bandit算法的效果:对同样的多臂问题,用不同的Bandit算法试验相同次数,看看谁的regret增长得慢。
那么到底不同的Bandit算法有哪些呢?
2)常用Bandit算法
Thompson sampling算法
Thompson sampling算法简单实用,因为它只有一行代码就可以实现[3]。简单介绍一下它的原理,要点如下:
- 假设每个臂是否产生收益,其背后有一个概率分布,产生收益的概率为p。
- 我们不断地试验,去估计出一个置信度较高的“概率p的概率分布”就能近似解决这个问题了。
- 怎么能估计“概率p的概率分布”呢? 答案是假设概率p的概率分布符合beta(wins, lose)分布,它有两个参数: wins, lose。
- 每个臂都维护一个beta分布的参数。每次试验后,选中一个臂,摇一下,有收益则该臂的wins增加1,否则该臂的lose增加1。
- 每次选择臂的方式是:用每个臂现有的beta分布产生一个随机数b,选择所有臂产生的随机数中最大的那个臂去摇。
UCB算法
UCB算法全称是Upper Confidence Bound(置信区间上界),它的算法步骤如下[4]:
- 初始化:先对每一个臂都试一遍;
- 按照如下公式计算每个臂的分数,然后选择分数最大的臂作为选择:
![]()
图3 UCB算法
- 观察选择结果,更新t和Tjt。其中加号前面是这个臂到目前的收益均值,后面的叫做bonus,本质上是均值的标准差,t是目前的试验次数,Tjt是这个臂被试次数。
这个公式反映一个特点:均值越大,标准差越小,被选中的概率会越来越大,同时哪些被选次数较少的臂也会得到试验机会。
Epsilon-Greedy算法
这是一个朴素的Bandit算法,有点类似模拟退火的思想:
- 选一个(0,1)之间较小的数作为epsilon;
- 每次以概率epsilon做一件事:所有臂中随机选一个;
- 每次以概率1-epsilon 选择截止到当前,平均收益最大的那个臂。
是不是简单粗暴?epsilon的值可以控制对Exploit和Explore的偏好程度。越接近0,越保守,只想花钱不想挣钱。
Greedy算法
先随机试若干次,计算每个臂的平均收益,一直选均值最大那个臂。这个算法是人类在实际中最常采用的,不可否认,它还是比随机乱猜要好。
3)Bandit算法Python实战
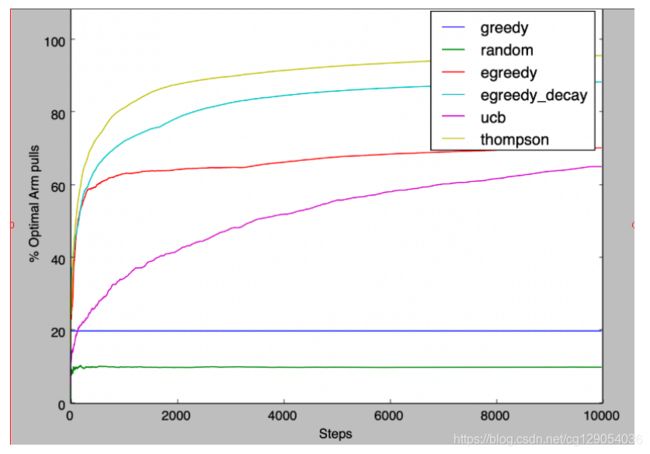
下面是我们模拟10000次的实验各种算法对比,可以看出Thompson算法效果是最好的。
import numpy as np
import matplotlib.pyplot as plt
import math
#老虎机个数
number_of_bandits=10
#每个老虎机的臂数
number_of_arms=10
#尝试数
number_of_pulls=10000
#eps
epsilon=0.3
#最小的decay
min_temp = 0.1
#衰减率
decay_rate=0.999
def pick_arm(q_values,counts,strategy,success,failure):
global epsilon
#随机返回一个臂
if strategy=="random":
return np.random.randint(0,len(q_values))
#贪心算法,每次都选取收益最大的那个臂
if strategy=="greedy":
best_arms_value = np.max(q_values)
#返回收益最大的臂的位置
best_arms = np.argwhere(q_values==best_arms_value).flatten()
#返回自身最大臂
# 等价于return best_arms[0]
return best_arms[np.random.randint(0,len(best_arms))]
#加epsilon,egreedy中,epsilon不变,egreedy_decay,epsilon变化
if strategy=="egreedy" or strategy=="egreedy_decay":
if strategy=="egreedy_decay":
epsilon=max(epsilon*decay_rate,min_temp)
if np.random.random() > epsilon:
best_arms_value = np.max(q_values)
best_arms = np.argwhere(q_values==best_arms_value).flatten()
return best_arms[np.random.randint(0,len(best_arms))]
else:
#以epsilon的概率随机选取一个臂
return np.random.randint(0,len(q_values))
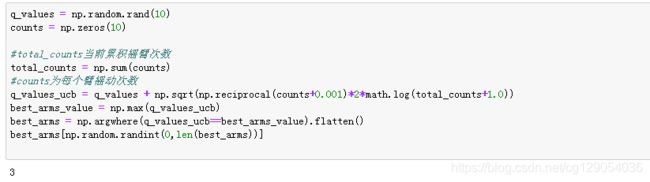
#ucb,按照ucb公式,算每个臂的收益,取最大的收益的臂/1000次除以10=1000
if strategy=="ucb":
total_counts = np.sum(counts)
q_values_ucb = q_values + np.sqrt(np.reciprocal(counts+0.001)*2*math.log(total_counts+1.0))
best_arms_value = np.max(q_values_ucb)
best_arms = np.argwhere(q_values_ucb==best_arms_value).flatten()
return best_arms[np.random.randint(0,len(best_arms))]
#thompson,利用beta分布选择臂
if strategy=="thompson":
sample_means = np.zeros(len(counts))
for i in range(len(counts)):
sample_means[i]=np.random.beta(success[i]+1,failure[i]+1)
return np.argmax(sample_means)
fig = plt.figure()
ax = fig.add_subplot(111)
for st in ["greedy","random","egreedy","egreedy_decay","ucb","thompson"]:
#定义 bandits个数*拉的次数的数组(10,10000)
best_arm_counts = np.zeros((number_of_bandits,number_of_pulls))
#对于每个老虎机来说(0,10)
for i in range(number_of_bandits):
#随机一个老虎机10个臂的收益w,保存最大收益
arm_means = np.random.rand(number_of_arms)
best_arm = np.argmax(arm_means)
#初始化臂的收益(10)为零
q_values = np.zeros(number_of_arms)
#初始化臂的拉动次数(10次)
counts = np.zeros(number_of_arms)
#初始化臂的成功次数
success=np.zeros(number_of_arms)
#初始化臂的失败次数
failure=np.zeros(number_of_arms)
#对于每次拉动
for j in range(number_of_pulls):
#根据不同的策略,选择臂a
a = pick_arm(q_values,counts,st,success,failure)
#当前臂a的收益,二项分布,收益为1或0
reward = np.random.binomial(1,arm_means[a])
#臂的次数+1
counts[a]+=1.0
#更新当前臂的收益(平均收益)
q_values[a]+= (reward-q_values[a])/counts[a]
#记录成功的收益
success[a]+=reward
#记录失败的收益
failure[a]+=(1-reward)
#更新best_arm_counts[i][j]
best_arm_counts[i][j] = counts[best_arm]*100.0/(j+1)
epsilon=0.3
#横纵坐标
ys = np.mean(best_arm_counts,axis=0)
xs = range(len(ys))
ax.plot(xs, ys,label = st)
plt.xlabel('Steps')
plt.ylabel('Optimal pulls')
plt.tight_layout()
plt.legend()
plt.ylim((0,110))
plt.show()
参考资料:
[1] https://blog.csdn.net/heyc861221/article/details/80129310
[2] https://en.wikipedia.org/wiki/Thompson_sampling
[3] http://nbviewer.jupyter.org/github/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers/blob/master/Chapter6_Priorities/Chapter6.ipynb#
[4] https://blog.csdn.net/a358463121/article/details/52562940
[5] https://blog.csdn.net/z1185196212/article/details/53374194