二连杆及三连杆的正逆运动学及雅可比

二连杆和三连杆是进行机器人控制中常用的模型，虽然机械臂大多是六轴，但是为了减轻求解复杂度，方便对算法的验证，仍会将六轴机械臂简化为两轴或者三轴的形式。

二连杆正逆运动学及雅可比

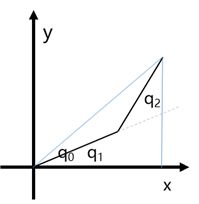
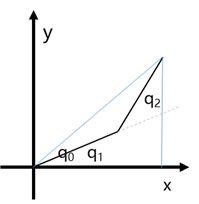
正运动学

function [x,y] = kin2(q1,q2,A)

a = A(1);
b = A(2);
x = acos(q1)+bcos(q1+q2);
y = asin(q1)+bsin(q1+q2);

end

微分运动学（雅可比）

function [J2] = dKin2(q1,q2,A)

a = A(1);
b = A(2);

J2 = zeros(2)
J2(1,1) = -asin(q1)-bsin(q1+q2);
J2(1,2) = -bsin(q1+q2);
J2(2,1) = acos(q1)+bcos(q1+q2);
J2(2,2) = bcos(q1+q2);

end

逆运动学

如图，由第二连杆末端向x轴做垂线，并连接第二连杆和原点，形成一个边长为 的直角三角形，记该直角三角形左下角为 ,有

求解q1

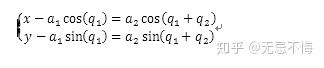
取平方并相加

对x和y进行替换并移项，得到

应用三角公式得到

得到

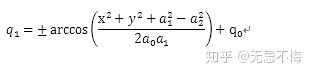公式1

求解q2

求解q1+q2的过程和求解q1是对称的，可以得到

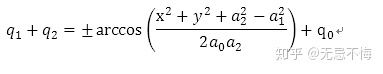
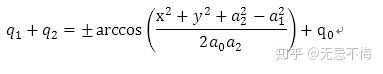
得到

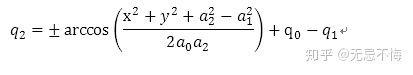
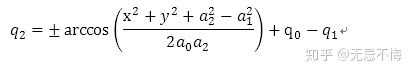公式2

但是这里并不是有四组解。由于

因此，公式1和公式2中的±号始终是相反的，仅有两组解。下面代码仅考虑q2>0

function [q1,q2] = iKin2(x,y,A)

a = A(1);
b = A(2);

q0 = atan2(y./x);
a0 = (x.^2+y.2).^0.5;

temp = (x.^2+y.2+a.^2-b.2)./(2*a0.*a);
q1 = -acos(temp)+q0;

temp = (x.^2+y.2-a.^2+b.2)./(2*a0.*b);
q2 = acos(temp)+q0-q1;

end

三连杆正逆运动学及雅可比

正运动学

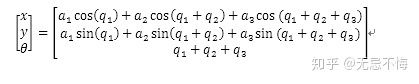
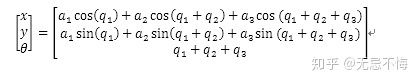
function [x,y,theta] = kin3(q1,q2,q3,A)

a = A(1);
b = A(2);
c = A(3);

x = acos(q1)+bcos(q1+q2)+ccos(q1+q2+q3);
y = asin(q1)+bsin(q1+q2)+csin(q1+q2+q3);
theta = q1+q2+q3;

end

微分运动学

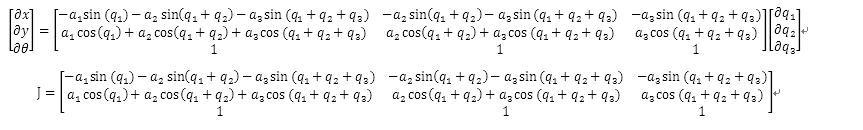
function [J3] = dKin3(q1,q2,q3,A)

a = A(1);
b = A(2);
c = A(3);

J3 = zeros(3)
J3(1,1) = -asin(q1)-bsin(q1+q2)-csin(q1+q2+q3);
J3(1,2) = -bsin(q1+q2)-csin(q1+q2+q3);
J3(1,3) = -csin(q1+q2+q3);

J3(2,1) = acos(q1)+bcos(q1+q2)+ccos(q1+q2+q3);
J3(2,2) = bcos(q1+q2)+ccos(q1+q2+q3);
J3(2,3) = ccos(q1+q2+q3);

J3(3,3) = 1;
J3(3,3) = 1;
J3(3,3) = 1;

end

逆运动学

三连杆的逆运动学可以化为二连杆的逆运动学进行求解。根据正运动学得到

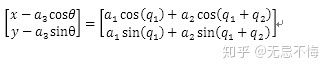
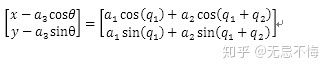
转变为一个二连杆运动学进行求解即可。仅考虑q2>0

function [q1,q2,q3] = iKin3(x,y,theta,A)

a = A(1);
b = A(2);
c = A(3);

xx = x-ccos(theta);
yy = y-csin(theta);
AA = [a,b];

[q1,q2] = iKin2(xx,yy,AA);
q3 = theta - q1 -q2;

end