pytorch1.7教程实验——DCGAN生成对抗网络

教程原网址：https://pytorch.apachecn.org/#/docs/1.7/22

DCGAN 是上述 GAN 的直接扩展，不同之处在于，DCGAN 分别在判别器和生成器中分别使用卷积和卷积转置层。 它最早由 Radford 等人，在论文《使用深度卷积生成对抗网络的无监督表示学习》中描述。 判别器由分层的卷积层，批量规范层和 LeakyReLU 激活组成。 输入是3x64x64的输入图像，输出是输入来自真实数据分布的标量概率。 生成器由转置卷积层，批量规范层和 ReLU 激活组成。 输入是从标准正态分布中提取的潜向量z，输出是3x64x64 RGB 图像。 跨步的转置层使潜向量可以转换为具有与图像相同形状的体积。 在本文中，作者还提供了一些有关如何设置优化器，如何计算损失函数以及如何初始化模型权重的提示，所有这些都将在接下来的部分中进行解释。

先贴上我跑通了的代码（如果中间有什么报错，这里不做解决方法说明）：

其中需要用到的celeba数据集的下载地址：http://mmlab.ie.cuhk.edu.hk/projects/CelebA.html
数据集网址打开后如下

这里有谷歌云盘和百度网盘两种方式下载，其中谷歌云盘不需登录，下载速度快，前提是可以，不然就用百度网盘，提取密码已给出。

from __future__ import print_function
#%matplotlib inline
import argparse
import os
import random
import torch
import torch.nn as nn
import torch.nn.parallel
import torch.backends.cudnn as cudnn
import torch.optim as optim
import torch.utils.data
import torchvision.datasets as dset
import torchvision.transforms as transforms
import torchvision.utils as vutils
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
# os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE" #注意会不会报libiomp5.dll的错误，会的话取消注释

# Set random seed for reproducibility
manualSeed = 999
#manualSeed = random.randint(1, 10000) # use if you want new results
print("Random Seed: ", manualSeed)
random.seed(manualSeed)
torch.manual_seed(manualSeed)


# Root directory for dataset
dataroot = "../data/celeba"

# Number of workers for dataloader
workers = 0

# Batch size during training
batch_size = 4

# Spatial size of training images. All images will be resized to this
#   size using a transformer.
image_size = 64

# Number of channels in the training images. For color images this is 3
nc = 3

# Size of z latent vector (i.e. size of generator input)
nz = 100

# Size of feature maps in generator
ngf = 64

# Size of feature maps in discriminator
ndf = 64

# Number of training epochs
num_epochs = 2

# Learning rate for optimizers
lr = 0.0002

# Beta1 hyperparam for Adam optimizers
beta1 = 0.5

# Number of GPUs available. Use 0 for CPU mode.
ngpu = 1


# We can use an image folder dataset the way we have it setup.
# Create the dataset
dataset = dset.ImageFolder(root=dataroot,
                           transform=transforms.Compose([
                               transforms.Resize(image_size),
                               transforms.CenterCrop(image_size),
                               transforms.ToTensor(),
                               transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
                           ]))
# Create the dataloader
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size,
                                         shuffle=True, num_workers=workers)

# Decide which device we want to run on
device = torch.device("cuda:0" if (torch.cuda.is_available() and ngpu > 0) else "cpu")

# Plot some training images
real_batch = next(iter(dataloader))
plt.figure(figsize=(8,8))
plt.axis("off")
plt.title("Training Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=2, normalize=True).cpu(),(1,2,0)))

# custom weights initialization called on netG and netD
def weights_init(m):
    classname = m.__class__.__name__
    if classname.find('Conv') != -1:
        nn.init.normal_(m.weight.data, 0.0, 0.02)
    elif classname.find('BatchNorm') != -1:
        nn.init.normal_(m.weight.data, 1.0, 0.02)
        nn.init.constant_(m.bias.data, 0)

# Generator Code

class Generator(nn.Module):
    def __init__(self, ngpu):
        super(Generator, self).__init__()
        self.ngpu = ngpu
        self.main = nn.Sequential(
            # input is Z, going into a convolution
            nn.ConvTranspose2d( nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # state size. (ngf*8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # state size. (ngf*4) x 8 x 8
            nn.ConvTranspose2d( ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # state size. (ngf*2) x 16 x 16
            nn.ConvTranspose2d( ngf * 2, ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # state size. (ngf) x 32 x 32
            nn.ConvTranspose2d( ngf, nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # state size. (nc) x 64 x 64
        )

    def forward(self, input):
        return self.main(input)

# Create the generator
netG = Generator(ngpu).to(device)

# Handle multi-gpu if desired
if (device.type == 'cuda') and (ngpu > 1):
    netG = nn.DataParallel(netG, list(range(ngpu)))

# Apply the weights_init function to randomly initialize all weights
#  to mean=0, stdev=0.2.
netG.apply(weights_init)

# Print the model
print(netG)

class Discriminator(nn.Module):
    def __init__(self, ngpu):
        super(Discriminator, self).__init__()
        self.ngpu = ngpu
        self.main = nn.Sequential(
            # input is (nc) x 64 x 64
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
        )

    def forward(self, input):
        return self.main(input)

# Create the Discriminator
netD = Discriminator(ngpu).to(device)

# Handle multi-gpu if desired
if (device.type == 'cuda') and (ngpu > 1):
    netD = nn.DataParallel(netD, list(range(ngpu)))

# Apply the weights_init function to randomly initialize all weights
#  to mean=0, stdev=0.2.
netD.apply(weights_init)

# Print the model
print(netD)


# Initialize BCELoss function
criterion = nn.BCELoss()

# Create batch of latent vectors that we will use to visualize
#  the progression of the generator
fixed_noise = torch.randn(64, nz, 1, 1, device=device)

# Establish convention for real and fake labels during training
real_label = 1.
fake_label = 0.

# Setup Adam optimizers for both G and D
optimizerD = optim.Adam(netD.parameters(), lr=lr, betas=(beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=lr, betas=(beta1, 0.999))


# Training Loop

# Lists to keep track of progress
img_list = []
G_losses = []
D_losses = []
iters = 0

print("Starting Training Loop...")
# For each epoch
for epoch in range(num_epochs):
    # For each batch in the dataloader
    for i, data in enumerate(dataloader, 0):

        ############################
        # (1) Update D network: maximize log(D(x)) + log(1 - D(G(z)))
        ###########################
        ## Train with all-real batch
        netD.zero_grad()
        # Format batch
        real_cpu = data[0].to(device)
        b_size = real_cpu.size(0)
        label = torch.full((b_size,), real_label, dtype=torch.float, device=device)
        # Forward pass real batch through D
        output = netD(real_cpu).view(-1)
        # Calculate loss on all-real batch
        errD_real = criterion(output, label)
        # Calculate gradients for D in backward pass
        errD_real.backward()
        D_x = output.mean().item()

        ## Train with all-fake batch
        # Generate batch of latent vectors
        noise = torch.randn(b_size, nz, 1, 1, device=device)
        # Generate fake image batch with G
        fake = netG(noise)
        label.fill_(fake_label)
        # Classify all fake batch with D
        output = netD(fake.detach()).view(-1)
        # Calculate D's loss on the all-fake batch
        errD_fake = criterion(output, label)
        # Calculate the gradients for this batch
        errD_fake.backward()
        D_G_z1 = output.mean().item()
        # Add the gradients from the all-real and all-fake batches
        errD = errD_real + errD_fake
        # Update D
        optimizerD.step()

        ############################
        # (2) Update G network: maximize log(D(G(z)))
        ###########################
        netG.zero_grad()
        label.fill_(real_label)  # fake labels are real for generator cost
        # Since we just updated D, perform another forward pass of all-fake batch through D
        output = netD(fake).view(-1)
        # Calculate G's loss based on this output
        errG = criterion(output, label)
        # Calculate gradients for G
        errG.backward()
        D_G_z2 = output.mean().item()
        # Update G
        optimizerG.step()

        # Output training stats
        if i % 50 == 0:
            print('[%d/%d][%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'
                  % (epoch, num_epochs, i, len(dataloader),
                     errD.item(), errG.item(), D_x, D_G_z1, D_G_z2))

        # Save Losses for plotting later
        G_losses.append(errG.item())
        D_losses.append(errD.item())

        # Check how the generator is doing by saving G's output on fixed_noise
        if (iters % 500 == 0) or ((epoch == num_epochs-1) and (i == len(dataloader)-1)):
            with torch.no_grad():
                fake = netG(fixed_noise).detach().cpu()
            img_list.append(vutils.make_grid(fake, padding=2, normalize=True))

        iters += 1


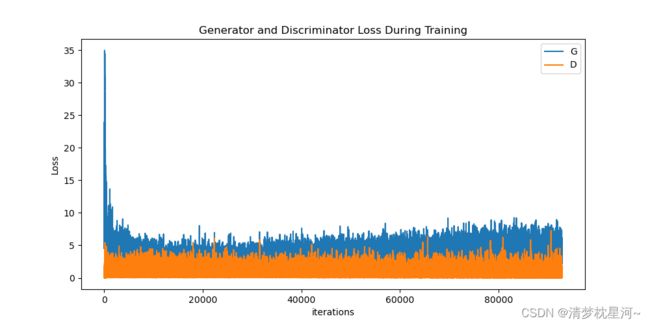
plt.figure(figsize=(10,5))
plt.title("Generator and Discriminator Loss During Training")
plt.plot(G_losses,label="G")
plt.plot(D_losses,label="D")
plt.xlabel("iterations")
plt.ylabel("Loss")
plt.legend()
plt.show()


#%%capture
fig = plt.figure(figsize=(8,8))
plt.axis("off")
ims = [[plt.imshow(np.transpose(i,(1,2,0)), animated=True)] for i in img_list]
ani = animation.ArtistAnimation(fig, ims, interval=1000, repeat_delay=1000, blit=True)

HTML(ani.to_jshtml())


# Grab a batch of real images from the dataloader
real_batch = next(iter(dataloader))

# Plot the real images
plt.figure(figsize=(15,15))
plt.subplot(1,2,1)
plt.axis("off")
plt.title("Real Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=5, normalize=True).cpu(),(1,2,0)))

# Plot the fake images from the last epoch
plt.subplot(1,2,2)
plt.axis("off")
plt.title("Fake Images")
plt.imshow(np.transpose(img_list[-1],(1,2,0)))
plt.show()

顺利执行时的效果如下：

mation, please see http://www.intel.com/software/products/support/.

D:\code\pytorch\dcgan
(pytorch) λ python dcgan.py
Random Seed:  999
Generator(
  (main): Sequential(
    (0): ConvTranspose2d(100, 512, kernel_size=(4, 4), stride=(1, 1), bias=False)
    (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (2): ReLU(inplace=True)
    (3): ConvTranspose2d(512, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (5): ReLU(inplace=True)
    (6): ConvTranspose2d(256, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (7): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (8): ReLU(inplace=True)
    (9): ConvTranspose2d(128, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (10): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (11): ReLU(inplace=True)
    (12): ConvTranspose2d(64, 3, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (13): Tanh()
  )
)
Discriminator(
  (main): Sequential(
    (0): Conv2d(3, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (1): LeakyReLU(negative_slope=0.2, inplace=True)
    (2): Conv2d(64, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (3): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (4): LeakyReLU(negative_slope=0.2, inplace=True)
    (5): Conv2d(128, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (6): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (7): LeakyReLU(negative_slope=0.2, inplace=True)
    (8): Conv2d(256, 512, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (9): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (10): LeakyReLU(negative_slope=0.2, inplace=True)
    (11): Conv2d(512, 1, kernel_size=(4, 4), stride=(1, 1), bias=False)
    (12): Sigmoid()
  )
)
Starting Training Loop...
[0/2][0/18579]  Loss_D: 1.3820  Loss_G: 12.0391 D(x): 0.8107    D(G(z)): 0.6061 / 0.0002
[0/2][50/18579] Loss_D: 0.0779  Loss_G: 7.6247  D(x): 0.9360    D(G(z)): 0.0039 / 0.0014
[0/2][100/18579]        Loss_D: 0.0260  Loss_G: 16.1513 D(x): 0.9753    D(G(z)): 0.0001 / 0.0000
[0/2][150/18579]        Loss_D: 0.0388  Loss_G: 13.1409 D(x): 0.9981    D(G(z)): 0.0346 / 0.0000
[0/2][200/18579]        Loss_D: 0.0162  Loss_G: 7.8809  D(x): 0.9849    D(G(z)): 0.0006 / 0.0025
[0/2][250/18579]        Loss_D: 0.0181  Loss_G: 9.7725  D(x): 0.9868    D(G(z)): 0.0047 / 0.0003
[0/2][300/18579]        Loss_D: 0.5012  Loss_G: 12.1612 D(x): 0.9483    D(G(z)): 0.3145 / 0.0000
[0/2][350/18579]        Loss_D: 1.1834  Loss_G: 4.7526  D(x): 0.6206    D(G(z)): 0.1919 / 0.0150
[0/2][400/18579]        Loss_D: 1.4490  Loss_G: 9.0369  D(x): 0.7937    D(G(z)): 0.3664 / 0.0001
[0/2][450/18579]        Loss_D: 1.0938  Loss_G: 9.3627  D(x): 0.9919    D(G(z)): 0.2552 / 0.0001
[0/2][500/18579]        Loss_D: 0.1821  Loss_G: 5.1612  D(x): 0.8762    D(G(z)): 0.0313 / 0.0122
[0/2][550/18579]        Loss_D: 0.9535  Loss_G: 4.7503  D(x): 0.5773    D(G(z)): 0.1484 / 0.0232
[0/2][600/18579]        Loss_D: 0.2484  Loss_G: 3.4991  D(x): 0.8649    D(G(z)): 0.0878 / 0.0408
[0/2][650/18579]        Loss_D: 3.4329  Loss_G: 8.1064  D(x): 0.8574    D(G(z)): 0.8436 / 0.0004
[0/2][700/18579]        Loss_D: 0.1063  Loss_G: 3.9823  D(x): 0.9932    D(G(z)): 0.0919 / 0.0203
[0/2][750/18579]        Loss_D: 0.3126  Loss_G: 3.1015  D(x): 0.8560    D(G(z)): 0.1302 / 0.0480
[0/2][800/18579]        Loss_D: 0.1231  Loss_G: 6.9449  D(x): 0.9156    D(G(z)): 0.0318 / 0.0028
[0/2][850/18579]        Loss_D: 0.4055  Loss_G: 2.5964  D(x): 0.7798    D(G(z)): 0.0892 / 0.0835
[0/2][900/18579]        Loss_D: 0.8483  Loss_G: 4.5182  D(x): 0.5921    D(G(z)): 0.0260 / 0.0207
[0/2][950/18579]        Loss_D: 1.5340  Loss_G: 1.5336  D(x): 0.3850    D(G(z)): 0.0217 / 0.2542
[0/2][1000/18579]       Loss_D: 1.8439  Loss_G: 6.5032  D(x): 0.4649    D(G(z)): 0.0024 / 0.0041
[0/2][1050/18579]       Loss_D: 0.4488  Loss_G: 4.1966  D(x): 0.8664    D(G(z)): 0.2313 / 0.0205
[0/2][1100/18579]       Loss_D: 0.3662  Loss_G: 3.8391  D(x): 0.8769    D(G(z)): 0.1729 / 0.0323
[0/2][1150/18579]       Loss_D: 0.9625  Loss_G: 4.0377  D(x): 0.6261    D(G(z)): 0.1720 / 0.0251
[0/2][1200/18579]       Loss_D: 0.6242  Loss_G: 2.7605  D(x): 0.7379    D(G(z)): 0.1765 / 0.0958
[0/2][1250/18579]       Loss_D: 2.9154  Loss_G: 7.8489  D(x): 0.9978    D(G(z)): 0.9003 / 0.0015
[0/2][1300/18579]       Loss_D: 0.6282  Loss_G: 5.1438  D(x): 0.8800    D(G(z)): 0.2477 / 0.0209
[0/2][1350/18579]       Loss_D: 2.0330  Loss_G: 2.2330  D(x): 0.2520    D(G(z)): 0.2362 / 0.1620
[0/2][1400/18579]       Loss_D: 0.1549  Loss_G: 5.1178  D(x): 0.9453    D(G(z)): 0.0848 / 0.0167
[0/2][1450/18579]       Loss_D: 0.1487  Loss_G: 4.1128  D(x): 0.9134    D(G(z)): 0.0419 / 0.0385
[0/2][1500/18579]       Loss_D: 0.1799  Loss_G: 6.6777  D(x): 0.8656    D(G(z)): 0.0030 / 0.0013
[0/2][1550/18579]       Loss_D: 0.3534  Loss_G: 3.4015  D(x): 0.8459    D(G(z)): 0.1279 / 0.0386
[0/2][1600/18579]       Loss_D: 0.5875  Loss_G: 4.9939  D(x): 0.7353    D(G(z)): 0.0743 / 0.0196
[0/2][1650/18579]       Loss_D: 0.3142  Loss_G: 5.3559  D(x): 0.7500    D(G(z)): 0.0065 / 0.0090
[0/2][1700/18579]       Loss_D: 0.6114  Loss_G: 3.8932  D(x): 0.8574    D(G(z)): 0.3115 / 0.0213
[0/2][1750/18579]       Loss_D: 0.6434  Loss_G: 6.0262  D(x): 0.6605    D(G(z)): 0.0581 / 0.0277
[0/2][1800/18579]       Loss_D: 0.4345  Loss_G: 4.2774  D(x): 0.8217    D(G(z)): 0.1581 / 0.0334
[0/2][1850/18579]       Loss_D: 0.1958  Loss_G: 4.5753  D(x): 0.8834    D(G(z)): 0.0593 / 0.0198
[0/2][1900/18579]       Loss_D: 0.9996  Loss_G: 5.7754  D(x): 0.8214    D(G(z)): 0.4628 / 0.0032
[0/2][1950/18579]       Loss_D: 0.7947  Loss_G: 4.2188  D(x): 0.7518    D(G(z)): 0.3216 / 0.0157
[0/2][2000/18579]       Loss_D: 0.2939  Loss_G: 3.2757  D(x): 0.9000    D(G(z)): 0.1616 / 0.0421
[0/2][2050/18579]       Loss_D: 0.5883  Loss_G: 4.5314  D(x): 0.7336    D(G(z)): 0.0686 / 0.0136
[0/2][2100/18579]       Loss_D: 0.6695  Loss_G: 2.0829  D(x): 0.6109    D(G(z)): 0.1248 / 0.2239
[0/2][2150/18579]       Loss_D: 2.0007  Loss_G: 2.0684  D(x): 0.1938    D(G(z)): 0.0221 / 0.2185
[0/2][2200/18579]       Loss_D: 1.1943  Loss_G: 2.6751  D(x): 0.3835    D(G(z)): 0.0441 / 0.0746
[0/2][2250/18579]       Loss_D: 0.9207  Loss_G: 4.7640  D(x): 0.7008    D(G(z)): 0.0192 / 0.0155
[0/2][2300/18579]       Loss_D: 0.1813  Loss_G: 3.1062  D(x): 0.9910    D(G(z)): 0.1548 / 0.0528
[0/2][2350/18579]       Loss_D: 0.5774  Loss_G: 2.8078  D(x): 0.7397    D(G(z)): 0.1623 / 0.0789
[0/2][2400/18579]       Loss_D: 0.6620  Loss_G: 3.4095  D(x): 0.9961    D(G(z)): 0.3208 / 0.0375
[0/2][2450/18579]       Loss_D: 0.2893  Loss_G: 3.8130  D(x): 0.9506    D(G(z)): 0.1999 / 0.0270
[0/2][2500/18579]       Loss_D: 1.6749  Loss_G: 3.2526  D(x): 0.4009    D(G(z)): 0.3853 / 0.0411
[0/2][2550/18579]       Loss_D: 0.5661  Loss_G: 4.9590  D(x): 0.9844    D(G(z)): 0.3471 / 0.0081
[0/2][2600/18579]       Loss_D: 0.4371  Loss_G: 3.0584  D(x): 0.7488    D(G(z)): 0.0928 / 0.0496
[0/2][2650/18579]       Loss_D: 0.9468  Loss_G: 3.0954  D(x): 0.6227    D(G(z)): 0.1914 / 0.0644
[0/2][2700/18579]       Loss_D: 1.2500  Loss_G: 5.9707  D(x): 0.9393    D(G(z)): 0.6179 / 0.0030

跑的过程中出现的相关结果图如下：




如果出现问题好好耐心地搜索强大的互联网，一般来说绝大多数问题都可解决。