使用线性回归、LGBM对二手车价格进行预测
使用线性回归、LGBM对二手车价格进行预测
目录
- 使用线性回归、LGBM对二手车价格进行预测
-
- 说明
- 数据导入、查看和清洗
-
- 数据说明
- 导入训练集
- 导入测试集
- 合并数据
- 查看数据整体情况
- 处理数据
-
- 检查并处理缺失变量
- EDA
-
- 年份和价格
- 地区和价格
- 前任里程和价格
- 燃料类型和价格
- 传动装置类型
- Mileage与价格
- 发动机排量与价格
- 特征编码
- 数据切分
- 模型建立
-
- 线性回归
- LGBM
- 数据和代码
- 专栏和往期项目
说明
本项目包含
1.数据处理
2.数据可视化
3.构建模型预测二手车价格
完整代码及数据见文末,可在线运行,也可下载
数据导入、查看和清洗
数据说明
column 列名
index 序号
Name 汽车的品牌和型号。
Location 该车正在销售或可购买的地点。
Year 车型的年份或版本。
Kilometers_Driven 前任车主驾驶该车的总公里数,单位为KM。
Fuel_Type 汽车使用的燃料类型(汽油/柴油/电动/CNG/LPG)。
Transmission 汽车使用的传动装置的类型。
Owner_Type 车主是否为第一手、第二手或其他。
Mileage 汽车公司提供的标准里程,单位是kmpl或km/kg。
Engine 发动机的排量,单位是cc。
Power 发动机的最大功率,单位是bhp。
Seats 汽车中的座位数。
New_Price 同一型号的新车的价格。
Price 二手车的价格,单位是印度卢比。( train.csv)
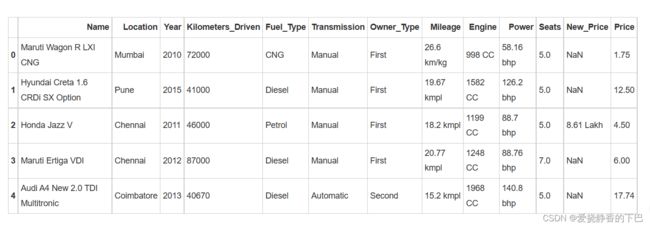
导入训练集
import pandas as pd
df_train = pd.read_csv('/home/mw/input/data6802/train-data.csv')
df_train.drop('Unnamed: 0',axis=1,inplace=True)
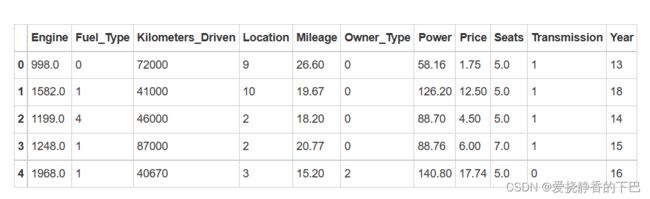
df_train.head()
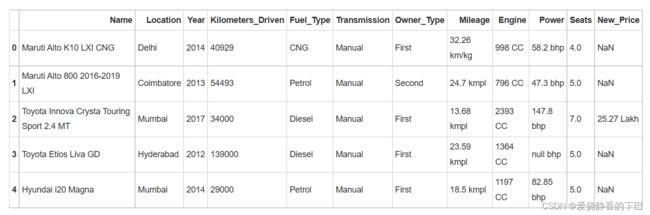
导入测试集
df_test = pd.read_csv('/home/mw/input/data6802/test-data.csv')
df_test.drop('Unnamed: 0',axis=1,inplace=True)
df_test.head()
合并数据
先合并数据,方便清洗
df = df_train.append(df_test)
df.head()
查看数据整体情况
查看数据缺失请况,可以看出,新车价格大面积缺失,缺失了86%,其余特征缺失率都较低
df.info()
Int64Index: 7253 entries, 0 to 1233
Data columns (total 13 columns):
Engine 7207 non-null object
Fuel_Type 7253 non-null object
Kilometers_Driven 7253 non-null int64
Location 7253 non-null object
Mileage 7251 non-null object
Name 7253 non-null object
New_Price 1006 non-null object
Owner_Type 7253 non-null object
Power 7207 non-null object
Price 6019 non-null float64
Seats 7200 non-null float64
Transmission 7253 non-null object
Year 7253 non-null int64
dtypes: float64(2), int64(2), object(9)
memory usage: 793.3+ KB
all_data_na = (df.isnull().sum()/len(df))*100
all_data_na = all_data_na.drop(all_data_na[all_data_na == 0].index).sort_values(ascending=False)
missing_data = pd.DataFrame({'缺失率' : all_data_na})
missing_data
缺失率
New_Price 86.129877
Price 17.013650
Seats 0.730732
Power 0.634220
Engine 0.634220
Mileage 0.027575
发现有一个重复数据,我们后面需要剔除掉
df.duplicated().sum()
处理数据
#去除重复值
df.drop_duplicates(inplace=True)
#删去缺失价格列和Name列
df.drop("New_Price", axis=1, inplace=True)
df.drop("Name", axis=1, inplace=True)
df.head()
检查并处理缺失变量
Seats、Power、Engine、Mileage
含义为:
Mileage 汽车公司提供的标准里程,单位是kmpl或km/kg。
Engine 发动机的排量,单位是cc。
Power 发动机的最大功率,单位是bhp。
Seats 汽车中的座位数。
不着急做填充,先挨个检查变量,然后进行处理
首先是车座
df['Seats'].value_counts()
5.0 6046
7.0 796
8.0 170
4.0 119
6.0 38
2.0 18
10.0 8
9.0 3
0.0 1
Name: Seats, dtype: int64
车座不可能为0,我们将其删除
df.drop(df[df['Seats']==0].index,axis=0,inplace=True)
df['Seats'].value_counts()
5.0 6046
7.0 796
8.0 170
4.0 119
6.0 38
2.0 18
10.0 8
9.0 3
Name: Seats, dtype: int64
剩余的缺失值我们用中位数填充
df['Seats'] = df['Seats'].fillna(df['Seats'].median())
df['Seats'].isnull().sum()
0
然后看看power,也就是发动机的最大功率
先把power的单位去除,再用中位数进行填补
df['Power'] = df['Power'].str.split(" ",expand=True)[0]
df['Power'] = pd.to_numeric(df['Power'],errors='coerce')
df['Power'].isnull().sum()
174
df['Power'] = df['Power'].fillna(df['Power'].median())
df['Power'].isnull().sum()
0
再来是Engine,发动机的排量,处理方式同上
df['Engine'] = df['Engine'].str.split(" ",expand=True)[0]
df['Engine'] = pd.to_numeric(df['Engine'],errors='coerce')
df['Engine'].isnull().sum()
46
df['Engine'] = df['Engine'].fillna(df['Engine'].median())
df['Engine'].isnull().sum()
0
Mileage 汽车公司提供的标准里程,单位是kmpl或km/kg。
df['Mileage'] = df['Mileage'].str.split(" ",expand=True)[0]
df['Mileage'] = pd.to_numeric(df['Mileage'],errors='coerce')
df['Mileage'].isnull().sum()
2
df['Mileage'] = df['Mileage'].fillna(df['Mileage'].median())
df['Mileage'].isnull().sum()
0
EDA
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
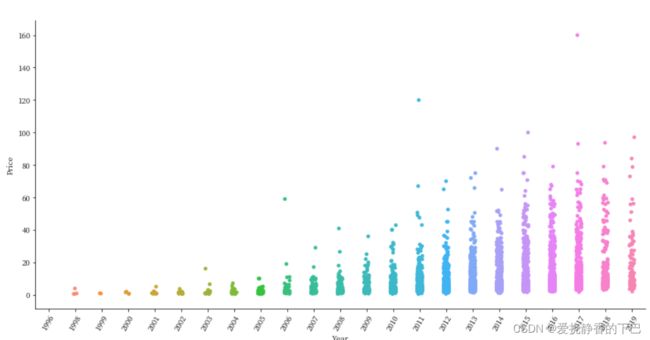
年份和价格
sns.catplot('Year', 'Price',height=6, aspect=2, data=df)
plt.xticks(rotation=60)
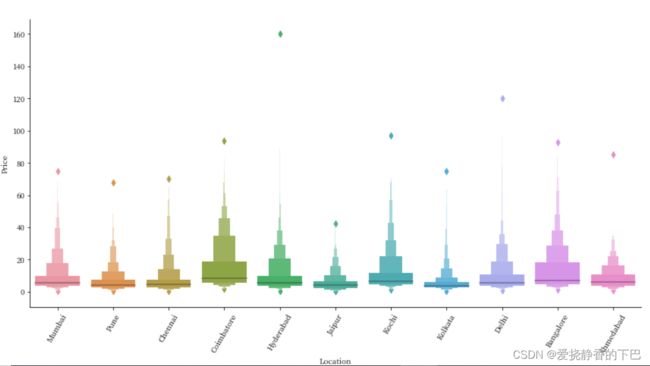
地区和价格
sns.catplot('Location', 'Price', kind="boxen",height=6, aspect=2, data=df)
plt.xticks(rotation=60)
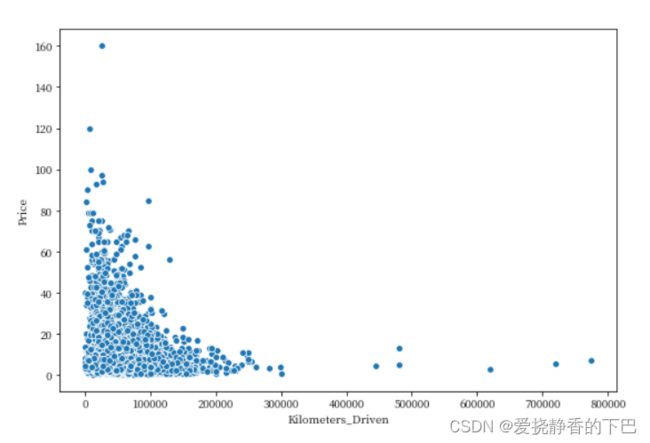
前任里程和价格
Kilometers_Driven 前任车主驾驶该车的总公里数
我们发现有个异常点,行驶超过了600万公里,我们以100W公里为分界线,将超出部分剔除再看看
df = df[df['Kilometers_Driven'] > 0]
df = df[df['Kilometers_Driven'] < 1000000]
plt.figure(figsize=(9,6))
sns.scatterplot('Kilometers_Driven', 'Price', data=df)
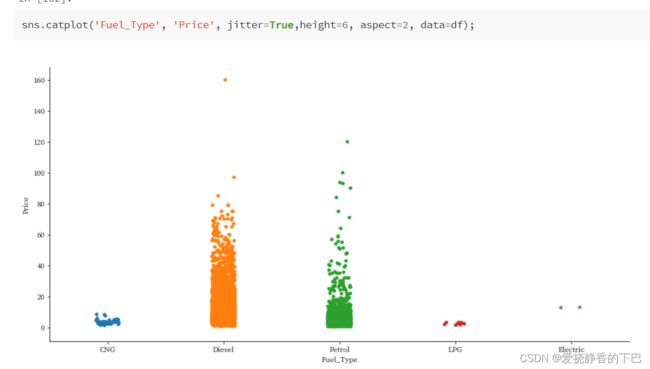
燃料类型和价格
Fuel_Type 汽车使用的燃料类型(汽油/柴油/电动/CNG/LPG)。
df['Fuel_Type'].value_counts()
Diesel 3851
Petrol 3323
CNG 62
LPG 12
Electric 2
Name: Fuel_Type, dtype: int64
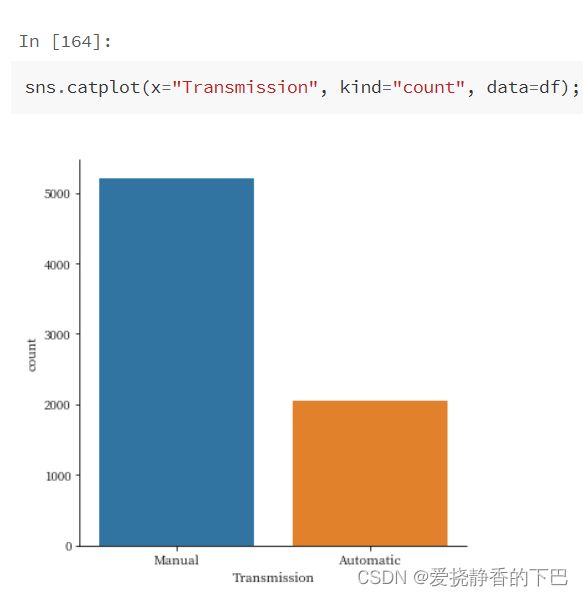
传动装置类型
Transmission 汽车使用的传动装置的类型。
df['Transmission'].value_counts()
Manual 5203
Automatic 2047
Name: Transmission, dtype: int64
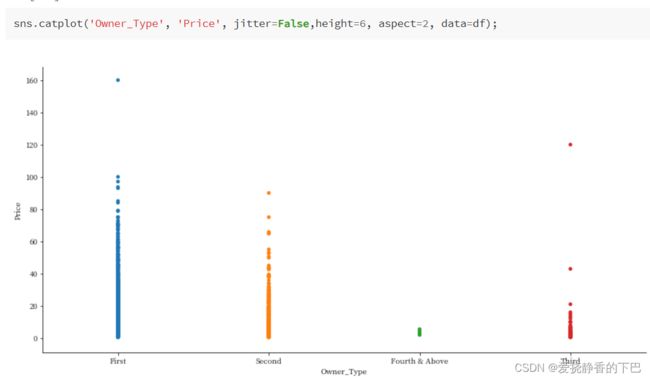
几手车主
Owner_Type 车主是否为第一手、第二手或其他。
df['Owner_Type'].value_counts()
First 5949
Second 1152
Third 137
Fourth & Above 12
Name: Owner_Type, dtype: int64
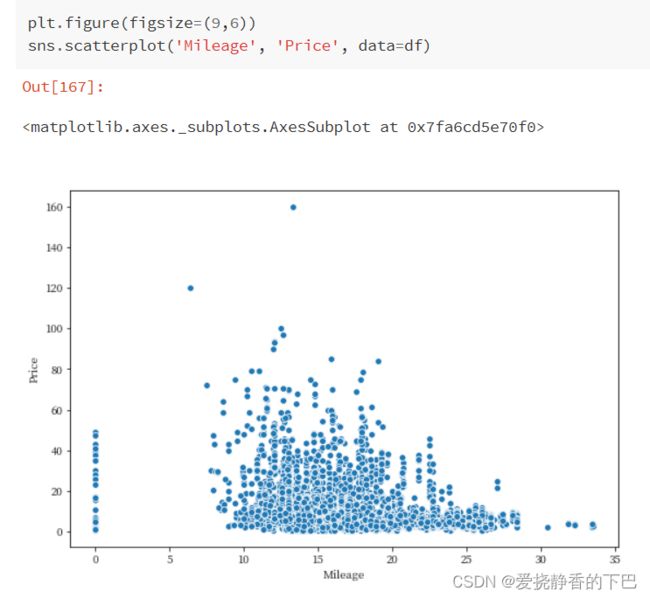
Mileage与价格
Mileage 汽车公司提供的标准里程,单位是kmpl或km/kg。
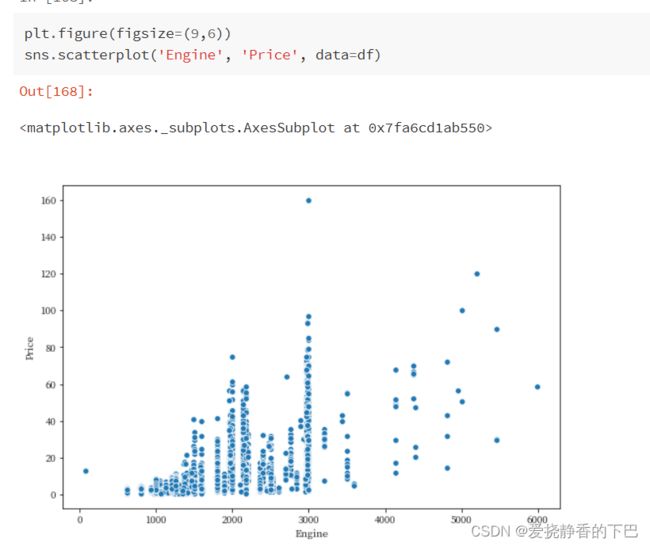
发动机排量与价格
Engine 发动机的排量,单位是cc。
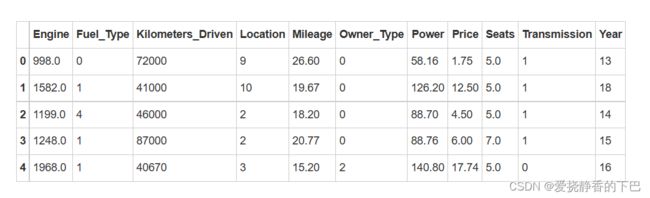
特征编码
from sklearn.preprocessing import LabelEncoder,OneHotEncoder
for feat in ['Fuel_Type', 'Location','Owner_Type', 'Transmission', 'Year']:
lbl = LabelEncoder()
lbl.fit(df[feat])
df[feat] = lbl.transform(df[feat])
df.head()
数据切分
df_train = df[~df['Price'].isnull()]
df_train = df_train.reset_index(drop=True)
df_test = df[df['Price'].isnull()]
df_train.head()
no_features = ['Price']
# 输入特征列
features = [col for col in df_train.columns if col not in no_features]
X = df_train[features] # 训练集输入
y = df_train['Price']# 训练集标签
X_test = df_test[features] # 测试集输入
from sklearn.model_selection import train_test_split
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.20, random_state=2022)
模型建立
线性回归
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train, y_train)
y_pred= lr.predict(X_val)
print("Score on Traing set: ",lr.score(X_train,y_train))
print("Score on valid set: ",lr.score(X_val,y_val))
Score on Traing set: 0.702077663498507
Score on valid set: 0.6982662108270392
from sklearn import metrics
from sklearn.metrics import mean_squared_error, mean_absolute_error
import numpy as np
print("\t\tError Table")
print('Mean Absolute Error : ', metrics.mean_absolute_error(y_pred,y_val))
print('Mean Squared Error : ', metrics.mean_squared_error(y_pred,y_val))
print('Root Mean Squared Error : ', np.sqrt(metrics.mean_squared_error(y_pred,y_val)))
print('R Squared Error : ', metrics.r2_score(y_pred,y_val))
Error Table
Mean Absolute Error : 3.8191025211006466
Mean Squared Error : 35.51327770962762
Root Mean Squared Error : 5.959301780378942
R Squared Error : 0.6092807923897521
LGBM
params = {
'learning_rate':0.1,
'n_estimators':1000,
'max_depth': 15,
'metric': 'mse',
'verbose': -1,
'seed': 2022,
'n_jobs': -1,
}
import lightgbm as lgb
model = lgb.LGBMRegressor(**params)
model.fit(X_train, y_train,
eval_set=[(X_train, y_train), (X_val, y_val)],
eval_metric='rmse',
verbose=50, early_stopping_rounds=100)
y_pred = model.predict(X_val, num_iteration=model.best_iteration_)
Training until validation scores don’t improve for 100 rounds.
[50] training’s rmse: 2.74657 training’s l2: 7.54363 valid_1’s rmse:
3.51272 valid_1’s l2: 12.3392 [100] training’s rmse: 2.20497 training’s l2: 4.86191 valid_1’s rmse: 3.22494 valid_1’s l2: 10.4002 [150] training’s rmse: 1.91286 training’s l2: 3.65904 valid_1’s rmse: 3.14442 valid_1’s l2: 9.8874 [200] training’s rmse: 1.7006 training’s l2: 2.89204 valid_1’s rmse: 3.10488 valid_1’s
l2: 9.64028 [250] training’s rmse: 1.5359 training’s l2:
2.35898 valid_1’s rmse: 3.09994 valid_1’s l2: 9.6096 [300] training’s rmse: 1.40321 training’s l2: 1.969 valid_1’s rmse: 3.13444 valid_1’s
l2: 9.82473 [350] training’s rmse: 1.2895 training’s l2:
1.66282 valid_1’s rmse: 3.15344 valid_1’s l2: 9.9442 Early stopping, best iteration is: [253] training’s rmse: 1.52763 training’s l2:
2.33365 valid_1’s rmse: 3.09248 valid_1’s l2: 9.5634
print("Score on Traing set: ",model.score(X_train,y_train))
print("Score on valid set: ",model.score(X_val,y_val))
Score on Traing set: 0.9815388772454189
Score on valid set: 0.9187458418102552
print("\t\tError Table")
print('Mean Absolute Error : ', metrics.mean_absolute_error(y_pred,y_val))
print('Mean Squared Error : ', metrics.mean_squared_error(y_pred,y_val))
print('Root Mean Squared Error : ', np.sqrt(metrics.mean_squared_error(y_pred,y_val)))
print('R Squared Error : ', metrics.r2_score(y_pred,y_val))
Error Table
Mean Absolute Error : 1.4166114668742893
Mean Squared Error : 9.563401874094804
Root Mean Squared Error : 3.092475040173292
R Squared Error : 0.9122361874546977
数据和代码
点击跳转代码,可在线运行
右上角Fork后可以获取全部代码
如果觉得还不错,可以点赞fork~
专栏和往期项目
往期文章可以关注我的专栏
下巴同学的数据加油小站
会不定期分享数据挖掘、机器学习、风控模型、深度学习、NLP等方向的学习项目,关注不一定能学到你想学的东西,但是可以学到我想学和正在学的东西