数据压缩|DPCM压缩系统的实现和分析

1.实验目的：用DPCM编码输出预测误差图像和重建图像。将预测误差图像写入文件并将该文件输入Huffman编码器，得到输出码流、给出概率分布图并计算压缩比。将原始图像文件输入Huffman编码器，得到输出码流、给出概率分布图并计算压缩比。

2.实验原理：

 在一个DPCM系统中，有两个因素需要设计：预测器和量化器。预测器采用左侧预测，采用8bit均匀量化。

3.代码实现：

量化以及预测部分：

int p,q,temp;
	for (int i = 0; i < h; i++) {
		re_y[i * w] = ori_y[i * w];
		err_b[i * w] = 0;
		for (int j = 1; j < w; j++) {
			p = ori_y[i * w + j] - re_y[i* w + j - 1];
			p = p / 2;
			q = p + 128;
			if (q < 0) {
				q = 0;
			}
			if (q > 255) {
				q = 255;
			}
			err_b[i * w + j] = q;
			p = p * 2;
			temp = re_y[i * w + j - 1] + p;
			if (temp < 0) {
				temp = 0;
			}
			if (temp > 255)
			{
				temp = 255;
			}
			re_y[i * w + j] = re_y[i * w + j - 1] + p;
		}
	}

计算PSNR和MSE：

double MSE = 0, PSNR = 0;
	for (int i = 0; i < h * w; i++) {
		MSE += pow(ori_y[i] - re_y[i], 2);
	}
	MSE /= (h * w);
	PSNR = 10 * log10((255 * 255) / MSE);
	cout << "MSE:" << MSE << endl;
	cout << "PSNR:" << PSNR << endl;

计算原图以及误差图像的概率分布：

	double fre_ori[256] = { 0 }, fre_q[256] = { 0 };
	frequency(ori_y,h*w, fre_ori);
	frequency(err_b, h*w, fre_q);

	//输出概率分布到csv

	fprintf(fp4, "Symbol,Frequency\n");
	fprintf(fp5, "Symbol,Frequency\n");

	for (int i = 0; i < 256; i++) {
		fprintf(fp4, "%-3d,%-8.2e\n", i, fre_ori[i]);
		fprintf(fp5, "%-3d,%-8.2e\n", i, fre_q[i]);
	}

头文件：

#include
void frequency(unsigned char* pic, int length, double* f) {
    for (int i = 0; i <= 255; i++) {
        for (int j = 0; j < length; j++) {
            if (pic[j] == i)f[i]++;
        }
        f[i] /= length;
    }
}

完整代码：

#include
#include"dpcm.h"
using namespace std;
int main(int argc, char* argv[])
{
	int w = 256;
	int h = 256;
	unsigned char* ori_y;
	unsigned char* re_y;
	unsigned char* err_b;
	unsigned char* u;
	unsigned char* v;
	ori_y = (unsigned char*)malloc(sizeof(unsigned char) * w * h);
	re_y = (unsigned char*)malloc(sizeof(unsigned char) * w * h);
	err_b = (unsigned char*)malloc(sizeof(unsigned char) * w * h);
	u = (unsigned char*)malloc(sizeof(unsigned char) * w * h / 4);
	v=(unsigned char*)malloc(sizeof(unsigned char) * w * h / 4);
	FILE* fp1 = NULL; 
	FILE* fp2 = NULL;
	FILE* fp3 = NULL;
	FILE* fp4=NULL;
	FILE* fp5=NULL;
	fopen_s(&fp1, argv[1], "rb");
	fopen_s(&fp2, argv[2], "wb");
	fopen_s(&fp3, argv[3], "wb");
	fopen_s(&fp4, argv[4], "wb");
	fopen_s(&fp5, argv[5], "wb");
	fread(ori_y, sizeof(unsigned char), h * w, fp1);
	for (int i = 0; i < w * h / 4; i++) {
		u[i] = 128;
		v[i] = 128;
	}
	int p,q,temp;
	for (int i = 0; i < h; i++) {
		re_y[i * w] = ori_y[i * w];
		err_b[i * w] = 0;
		for (int j = 1; j < w; j++) {
			p = ori_y[i * w + j] - re_y[i* w + j - 1];
			p = p / 2;
			q = p + 128;
			if (q < 0) {
				q = 0;
			}
			if (q > 255) {
				q = 255;
			}
			err_b[i * w + j] = q;
			p = p * 2;
			temp = re_y[i * w + j - 1] + p;
			if (temp < 0) {
				temp = 0;
			}
			if (temp > 255)
			{
				temp = 255;
			}
			re_y[i * w + j] = re_y[i * w + j - 1] + p;
		}
	}
	fwrite(err_b, sizeof(unsigned char), w * h, fp2);
	fwrite(u, sizeof(unsigned char), w * h/4, fp2);
	fwrite(v, sizeof(unsigned char), w * h/4, fp2);

	fwrite(re_y, sizeof(unsigned char), w * h, fp3);
	fwrite(u, sizeof(unsigned char), w * h / 4, fp3);
	fwrite(v, sizeof(unsigned char), w * h / 4, fp3);

	//计算MSE,PSNR
	double MSE = 0, PSNR = 0;
	for (int i = 0; i < h * w; i++) {
		MSE += pow(ori_y[i] - re_y[i], 2);
	}
	MSE /= (h * w);
	PSNR = 10 * log10((255 * 255) / MSE);
	cout << "MSE:" << MSE << endl;
	cout << "PSNR:" << PSNR << endl;
	
	//计算概率分布
	double fre_ori[256] = { 0 }, fre_q[256] = { 0 };
	frequency(ori_y,h*w, fre_ori);
	frequency(err_b, h*w, fre_q);

	//输出概率分布到csv

	fprintf(fp4, "Symbol,Frequency\n");
	fprintf(fp5, "Symbol,Frequency\n");

	for (int i = 0; i < 256; i++) {
		fprintf(fp4, "%-3d,%-8.2e\n", i, fre_ori[i]);
		fprintf(fp5, "%-3d,%-8.2e\n", i, fre_q[i]);
	}




}

4.图像结果：

实验图像如上图所示，分别为原图，误差图像和重建图像。MSE为0.496，PSNR为51.1772。

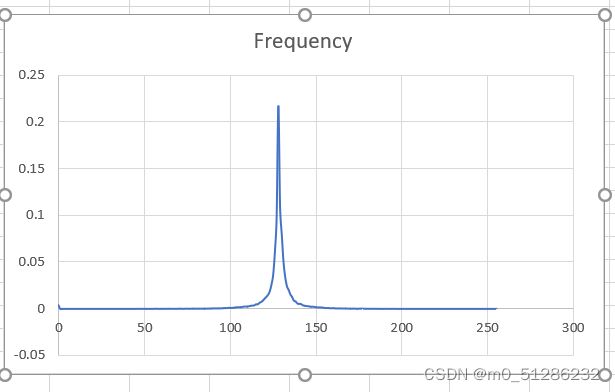
下图为原图以及误差图像的概率分布：可以看出误差图像概率分布比较集中。

 

5.原图以及误差图像经过Huffman编码后如下图所示：原图压缩比为：1.39；误差图像为：2.23。可以看出误差图像的压缩效率要比直接进行Huffman编码的效率高。