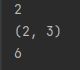从头开始学人工智能day02

从头开始学人工智能

---

第二天，补充numpy学习

选择编程工具（jupyter notebook或者idea）

介绍numpy

NumPy是使用Python进行科学计算的基础包。它包含如下的内容：

• 一个强大的N维数组对象。
• 复杂的（广播）功能。
• 用于集成C / C ++和Fortran代码的工具。
• 有用的线性代数，傅里叶变换和随机数功能。

除了明显的科学用途外，NumPy还可以用作通用数据的高效多维容器。可以定义任意数据类型。这使NumPy能够无缝快速地与各种数据库集成。

NumPy是在BSD许可下获得许可的，允许重用而不受限制。

搭建环境（开启征程）

导库

import numpy as np

使用array

创建一维数组

#创建一维数组
arr = np.array([12,23,34],dtype="int32")
print(arr)
print(arr.dtype)

这里前面的参数value是数组数据，后面的dtype是数组的数据类型，默认就是32位的int

使用多维数组

#创建多维数组
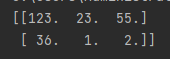
arrs =np.array([[123,23,55],[36,1,2]],dtype="float")
print(arrs)
print(arrs.dtype)

基本与一些语言的二维数组一致，python的列表

这里的dtype是float64 ，不做解释

使用全零数组

#创建全零数组
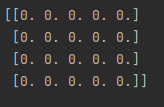
zeros = np.zeros((4,5))
print(zeros)

生成的是4行5列的全零数组，参数一是shape(形状)，也就是几行几列，好吧！思考一下，一列怎么生成？

使用全一数组

#创建全一数组
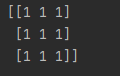
ones = np.ones((4,4),dtype = "int32")
print(ones)

使用全空数组

#创建全空数组
emptys = np.empty((3,4))
print(emptys)

为什么会生成这样的数？好吧，其他的参数都不解释，这里生成的都是随机的，但特点就是都接近零的数！

使用连续数组

#创建连续数组
nums = np.arange(1,10,1)
print(nums)

左闭右开的方式，以步长为1的方式生成数组，参数是start,end,step表示开始值，结束值，步长

使用随机数组

#创建随机矩阵
randomArr = np.random.random((2,4))
print(randomArr)

使用reshape

这里解释一下，re前缀一般表示重新做啥事！这里可以理解为重新定义形状！

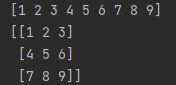
#使用reshape将nums定义为3*3的矩阵
changeNums = nums.reshape((3,3))
print(changeNums)

注意，这里要保证可以合理分配！

使用linspace

既然有了改变结构的respace，为什么不能有切割数据的linspace呢？

#等分一个数据
arr = np.linspace(9,20,13)
print(arr)

print("----------------------------------------------------")
#等分一个数据
arr2 = np.linspace(9,20,12)
print(arr2)

做一个对比，不难发现，都是全包含的区间等分多少份的数据！

里面的参数有start,end,step看图，不做解释

结合respace和linspace使用一下

#结合respce和linspace一起使用
arrs = arr2.reshape(3,4)
print(arrs)

数组方面就结束了，但操作空间大啊！我们继续学习！

数组基本操作

列表转为矩阵

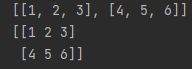
pynums = [[1,2,3],[4,5,6]] #原生python的列表
npnums = np.array(pynums)
print(pynums)
print("-------------------------------")
print(npnums)

矩阵的维度，形状，大小

print(npnums.ndim)
print(npnums.shape)
print(npnums.size)

dim是维度，shape就是形状，size就是大小

基本矩阵运算

一维矩阵运算

加法运算

a = np.arange(0,4,1)
b = np.arange(4,8,1)
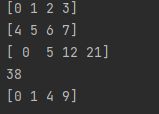
print(a)
print(b)
c = a+b
print(c)

其他的运算差不多！！！

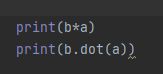
这里需要注意一下，b*a就是矩阵，而b.dat(a)是先将计算出来的矩阵做和运算得到一个值，这个函数一般用于多维矩阵运算，也就是多维矩阵的乘法

平方，也就是幂运算，也是一致的，生成矩阵

数学函数

print(np.cos(a))

布尔判断

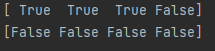
print(a<3)
print(a==b)

多维矩阵运算

矩阵乘法

#多维矩阵运算
nums = np.arange(1,10,1).reshape(3,3)
arrs = np.array([
    [10,11,12],
    [13,14,15],
    [16,17,18],
])
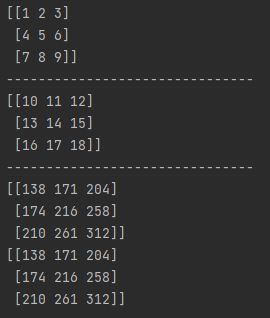
print(nums)
print("-------------------------------")
print(arrs)
print("-------------------------------")
print(arrs.dot(nums))
print(np.dot(arrs,nums))

这里使用的dot就是一个矩阵乘法，关于矩阵乘法在线性代数就有介绍，也不做解释

矩阵元素求和

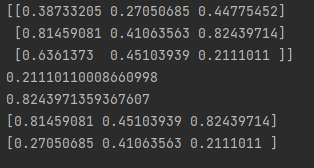
randomArr = np.random.random((3,3))
print(randomArr)
print(np.sum(randomArr))

这里直接使用了sum函数

下面的min，max以及各维度上进行操作都快速带过

print(np.min(randomArr))
print(np.max(randomArr))

print(np.max(randomArr,axis=0))#0代表以列为查找单位查找
print(np.min(randomArr,axis=1))#1代表以行为查找单位查找

这里可以进行一下比对，将这个矩阵完全打印在上方了

关于多维矩阵运算也就到这了

基本计算

直接使用一些函数做运算

这里不多做解释，一起来学习就好了！

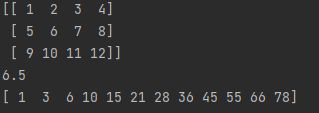
arr = np.arange(1,13).reshape(3,4)
print(arr)

#下面的两种写法都是返回矩阵最小元素的下标
print(np.argmin(arr))
print(arr.argmin())

#x效果与上相反
print(np.argmax(arr))
print(arr.argmax())

#下面都是返回矩阵的均值
print(np.mean(arr))
print(arr.mean())
#这种很好理解，我比较喜欢
print(np.average(arr))

这里不做过多的解释，都很好理解

下面的就是一些对我来说的陌生函数了

#中位数
print(np.median(arr))

#累加
print(np.cumsum(arr))

中位数的话，这里选的数据可能不是很理想，但却是是中位数，累加的话要解释一下，也就是从当前索引向前面的一直遍历相加，得当当前索引的值，切记，这里得到的是一个一维数组

#累差
print(np.diff(arr))

这里也解释一下，可以发现，3*4的矩阵变成了3*3的矩阵了！

所以我们可以看出，缺了一列，那就必有运算，得到第一列就是用过第二列减去第一列的数字实现的，所以为什么是3列就很容易理解了！我们继续学习

#排序
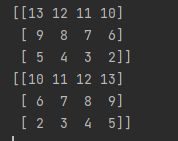
nums = np.arange(13,1,-1).reshape(3,4)
print(nums)
print(np.sort(nums))

这里是将矩阵的每一秩（行）都按升序排序

矩阵转置

这应该是个重点，学过线性代数都应该对他不陌生

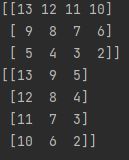
nums = np.arange(13, 1, -1).reshape(3, 4)
print(nums)

#矩阵转置
print(np.transpose(nums))

#这里可以说一下，转置的符号是T，所以这里是支持直接使用T的，效果是与下面一样
print(nums.T)

numpy索引和切片

简单索引

nums = np.arange(13, 1, -1).reshape(3, 4)
print(nums[0])

#下面都是索引0行2列
print(nums[0][2])
print(nums[0,2])

这就和数组下标索引一样，问题不大

切片操作

#第0行1~3的左闭右开的数据
print(nums[0,1:3])

#在知道有一维矩阵转成多维矩阵的reshape后，这里还有一个扁平化处理的flatten
print(nums.flatten())

#快速将一个多维矩阵降维成一列
for i in nums.flat:
    print(i)

小结一下

numpy这个入门算是到这里了，明天我们再接再厉，将numpy后面的知识也全部学完，明天还有蓝桥杯比赛，当然，我还是选择了我的java，明天好运！

记录于2022 04 08