从头开始学人工智能day05
从头开始学人工智能
文章目录
- 从头开始学人工智能
-
- 今日学习目标!
-
- 序
- 机器学习分类
- 1.1线性模型
-
- 1.1.1普通最小二乘法(分类算法)
- 通俗易懂学习最小二乘法
-
- 先了解一下最小二乘!
- 使用最小二乘预测
-
- 总结
今日学习目标!
序
前面我们已经简单学习了numpy,pandas,matplotlib,在我学习java的时候都是跟着视频去敲过来的,后面需要自己思考,接着就是看源码,源码基本都在啃书,后面就不再喜欢看视频了,毕竟书的话才算是第一数据来源吧!至于java学的怎么样,也就是看了spring和mybaits源码,然后自己慢慢自己敲,感觉还是蛮不错的!反正现在是喜欢去看书!这个都是看自己的爱好的吧!之前也是跟着老师去研究研究算法,一些单目标,多目标算法,当时的话还是觉得工程好玩,现在的话,我会毫不犹豫的选择算法!真香定理吧!一些传统算法还是可以的,这次蓝桥杯确实打击有点大!不管不管!静下心一起学习!说这么多就是想说,我们可以先跳到这个有成就感的地方来入门这个,随着使用巩固前面的知识,加深前面的知识!至于不会的知识可以去自己了解!去补充!好吧不多说啦!
机器学习分类
是否在人类监督下进行训练(监督,无监督和强化学习)
在机器学习中,无监督学习就是聚类,事先不知道样本的类别,通过某种办法,把相似的样本放在一起归位一类;而监督型学习就是有训练样本,带有属性标签,也可以理解成样本有输入有输出。
所有的回归算法和分类算法都属于监督学习。回归和分类的算法区别在于输出变量的类型,定量输出称为回归,或者说是连续变量预测;定性输出称为分类,或者说是离散变量预测
1.1线性模型
1.1.1普通最小二乘法(分类算法)
这里解释一下分类算法!
分类是一个有监督的学习过程,目标数据库中有哪些类别是已知的,分类过程需要做的就是把每一条记录归到对应的类别之中。由于必须事先知道各个类别的信息,并且所有待分类的数据条目都默认有对应的类别,因此分类算法也有其局限性,当上述条件无法满足时,我们就需要尝试聚类分析。
(还有一种聚类算法!后话啦)简单的说,就是没有标签,然后在一块的就算一类
解释一下最小二乘法
用产生该样本概率最大的原则确定样本回归模型,称为极大似然准则;用使估计的残差平方和最小的原则确定样本回归模型,称为最小二乘准则。此书,仅介绍在古典假定条件下的最小二乘准则,也称为普通最小二乘估计,简记为OLS估计(ordinary least suqares estimators)。
通俗易懂学习最小二乘法
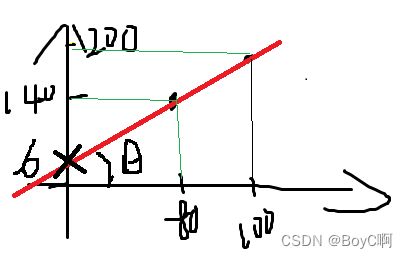
假定有一栋房子现在面积是100平方米,他现在出售可以的到200万。这里给我们的第一信息就是一平米是2万!可以得到一个公式!
y=2*x
Y:价格;x:面积;
假定这个公式是正确的,这时候有另一房子70平方米,而现在要报价出售,对于营销商来说,要更高的价格而且要保证可以卖出去(买家拥有绝对的智商),所以我们可以通过上面那个公式预测出报价多少不会亏也会让消费者接受!
当 x = 70时候 ==>y = 140
所以就可以知道报价啦!
如果理解了上面的过程,那么我们就可以提到训练和模型了!
训练:上面提到一个公式,而这个公式怎么来的,可以知道,他是通过100 —> 200的过程得到的!也就是说,通过一个自变量和一个因变量就可以知道这个公式!至于数据怎么来,后面继续!而得到这个公式的过程就是训练!
模型:对于这个我也不是很明确,我的理解就是一个过程,通过这个过程就可以得到目标值!也就是这里的公式!对于这里的线性模型可以理解为一个权值!也就是单价!
那假设上面的公式是错误的呢!
在没有这个公式是没出来的时候,有两栋房子,一栋100平方米!卖了200万,另一栋80平方米!卖了140万!
这里的话就没办法去使用一个线性的模型去完全拟合这两个参数了!
但这里就是需要线性模型怎么办!
整呗~!!
根据一平方米的单价来尽可能的符合他们!
也就是
Y = ?* x;
这里加入?便是拟合后的数据,至于怎么拟合的看后话!
但是都不准!也就是100的话也不匹配!80也不匹配!但是他是让他们的误差最小的!误差定义也看后话!
这里要解释的仅仅是对于线性模型的不足!很难做到完全拟合!
要说拟合不了!~~nonono
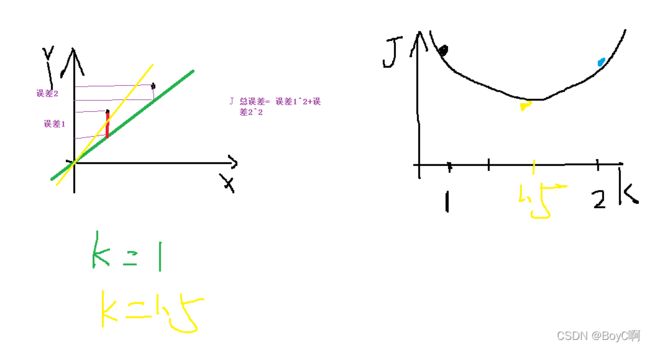
如果我们在加一个参数呢!(看图)
这里加啦一个参数b是不是将两个点拟合了!
也就是说不同的数据值拟合出来的模拟的向量是不同的!
得到的参数也就是【k,b】也就是斜率和偏移量!
经过啦这样的解说!现在对于这个也就有了一定的认识!
实际的最小二乘,也就是通过一堆的数据(不只是两个)去拟合(喂养)一个模型出来,然后使用这个模拟去做预测测试!
而更多时候,决定一个因变量的值的不仅仅是一个参数!也就是不仅仅是x决定y,可以是x,y去决定z,想不想二元一次方程!
而这里的参数就会是一个向量【x.y】
拟合出来的数据上面已经提过也就是一个模拟w【】的向量!
先了解一下最小二乘!
Y_TRAIN:表示Y的训练向量
X_TRAIN:表示X的训练向量
Y_TRAIN = X_TRAIN*K+B;
这里要得到的就是K和B!
假如初始化一个K和B
通过K和B求得的Y_p(预测值)和Y_t就应该保证误差越小越好!
他们的误差也就是(回归残差)e = Y_p - Y_t;
这里的e有正有负,所以就取e的平方,后面的E就代表e的平方
得到公式
min.Math.sum(E) = min.Math.sum(Y_p-Y_t)^2 = min.Math.sum(Y_p-X_t*K-B);
上面这个函数现在定为S(K,B);
通过高等数学的求极值的方法,要使min.sum(E)则K,B满足:
{
分别对K和B求偏导后得0;
}
得到方程:
sum(Y_p) = nB+K*sum(X_t)
sum(Y_p*X_t) = Bsum(X_t)+Ksum(X_t^2)
最后得到Y_p = B+K*X_t+e;
简单的来说,每次变化一点,慢慢拟合
就假如我们现在K是1;误差是100,把这两个值画一个新的坐标轴,然后可以得到一根二次曲线,而两个参数的K,B就会得到一个三维的坐标系!
看图
这里对[K,J]函数的k=1的切点求导,然后用 J原来-J更新 比较一下,判断是否更新,这样基本就能达到局部最优!为毛是局部最优,后话后话,可以细想想为啥为啥减去求导就会靠近优解,再想想有什么问题!这也就是熟悉的一种,梯度下降算法!
使用最小二乘预测
# Code source: Jaques Grobler
# License: BSD 3 clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Load the diabetes dataset
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)
# Use only one feature
#冒号在前,列项
diabetes_X = diabetes_X[:, np.newaxis, 2]
# Split the data into training/testing sets
print("-------------------------------------")
diabetes_X_train = diabetes_X[:-20]
print(len(diabetes_X_train))
diabetes_X_test = diabetes_X[-20:]
print("-------------------------------------")
print(len(diabetes_X_test))
# Split the targets into training/testing sets
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
#拟合模型(使用训练集训练模型)
regr.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
#预测值
diabetes_y_pred = regr.predict(diabetes_X_test)
# The coefficients
print('Coefficients: \n', regr.coef_)
# The mean squared error
print('Mean squared error: %.2f'
% mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print('Coefficient of determination: %.2f'
% r2_score(diabetes_y_test, diabetes_y_pred))
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
代码来自:线性回归实例-scikit-learn中文社区
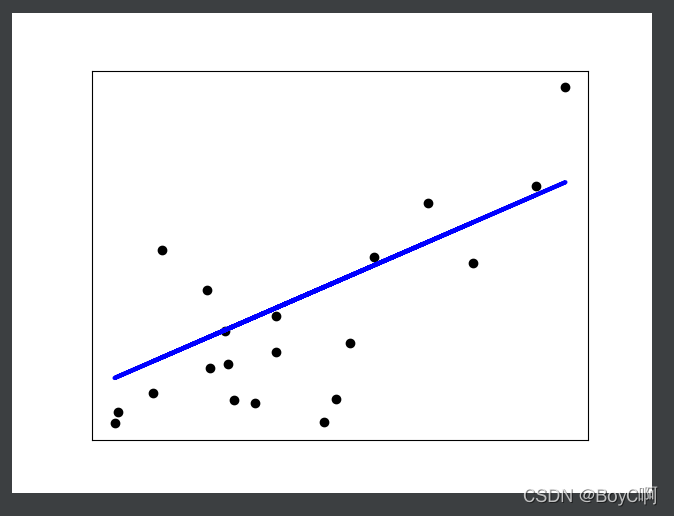
过程就是先引入数据集,一部分用于训练(422),一部分用于预测(20),然后比较预测值和实际值的误差,在显示出来误差和时间!最后作图!一起练练~
拟合图
总结
最小二乘线性回归里面的基本算法!具体的代码思路我们要多练练!最近就在慢慢啃这个和比赛!哈哈哈,一起加油!
记录于 2022 04 13