从头开始学人工智能day06

从头开始学人工智能

今日目标！

序

前面学习了机器学习的入门算法，这次是一个与他大同小异的一个算法！（梯度下降），这里我们学习的是简单的一维的线性拟合！

开启征程

梯度下降法介绍！

梯度下降法（Gradient Descent，GD）是一种常用的求解无约束最优化问题的方法，在最优化、统计学以及机器学习等领域有着广泛的应用。本文将深入浅出的为读者介绍梯度下降法的原理。

大部分的机器算法或多或少都会有一些梯度下降的思想！而梯度下降具体怎么用，具体实现是怎么样的！这里我慢慢学了一下！其实蛮好理解的！

明确问题

还是同一个例子

这里有10斤苹果，然后卖了20元，第一眼就可以知道单价是2元一斤！

得到第一个公式

Y = 2*X

这时候又有一堆苹果！14斤，卖了30元，这里的话上面那个公式就不能符合这个公式了！

这里如果继续使用这个函数的话，一定会有误差（均方差）但也会有一个误差最小的线，这里如果不加入新的参数，那么就是找出这个误差最小时的线方程（斜率就好）！

如果加一个新的参数的话！那么只需要加入一个常数B就可以拟合一根直线出来！

得到的模型也就是

Y = Kx+B

而找到这个模型的方法之中就会有梯度下降的方法！

解题思路

这里定义一个X_Y的二维坐标系！

X：重量

Y：价格

这里因为误差有正有负，所以就采用均方差（1/(2*len(粒子集))）*（J1^2+J2^2）

推导公式：

J：J = 1/(2*m)*sum((H(x)-J(x))^2)

这里的h(x)当作预测好的模型预测的值，而j(x)表示为实际值，公式表达就是求所有误差和求均方！

而我们得到这个的话只能求到偏差多少！那怎么利用！

答案就是再来一个图！

这里的参数Y一定是J（代价函数），自变量就是需要拟合的向量（有可能不是一个变量影响J 的！见上面）

这里的每个斜率都会有一个代价值，而我们就是要找到代价值最小的K

很简单，极值嘛！那如果不是标准的二元函数呢！这里的话我们就要用梯度下降的思想！

使代价函数对K值求偏导！有多参数的话分别求偏导，每个方向更新就好！

这里倒数就是切线，而切线为零的时候就是我们要的点啦！但这样还是会有问题！就是我们怎么更新这个K呢！很简单！贪心的想法！

先记录一下本来存在的代价值，在计算一下更新后的代价值！最后比较谁小！如果更新后小的话！我就实际更新K，不然我就进行调整！

这里解决了更新！

我们也要明确更新多少！相信大家都知道！更新速度太慢，则收敛太慢！也就要算很久！太快的话就会发散！也就是压根不会收敛！

所以我们就采用0.1，0.01…这样慢慢调整，而上面提到的调整学习速度就是调整这个，好吧，屁话不多说，还是模拟一下代码来的简单理解！

代码

import numpy as np
import matplotlib.pyplot as plt

if __name__ =="__main__":
    '''
    单参数的线性拟合梯度下降
    y = K*x
    '''
    # 导入数据
    X_train = np.arange(1,11,1)
    Y_train = np.array([2,5,7,9,12,13,15,17,20,23])

    print(X_train)
    print(Y_train)

    K = 0 #初始化K
    m = 10#粒子个数
    W = 0.01 #学习速度
    def update(K,w):
        """
        通过更新代价值来计算
        :return:
        """
        J=0 #代价函数
        a=0 #导数
        Y_p=[] #原来的预测值
        
        #计算预测Y
        for i in range(10):
            Y_p.append(X_train[i]*K)

        #计算代价
        for i in range(10):
            J += ((1 / (m * 2) )* pow(Y_p[i] - Y_train[i], 2))

        #计算导数
        for i in range(10):
            a+=((1/m)*(Y_p[i]-Y_train[i])*X_train[i])

        temp = K - w*a
        # print(temp)
        
        Jc = 0  #更新后的代价值
        Y_P = []  #更新后的预测值存储
        
        #计算更新后的预测值
        for i in range(10):
            Y_P.append(X_train[i]*temp)

        #计算更新后的代价
        for i in range(10):
            Jc+=(1/(m*2))*pow(Y_P[i]-Y_train[i],2)

        #判断是否更新
        if(Jc<J):
            #实际更新
            K = temp
        else:
            #调整
            w/=10

        print("初始化",J)
        print("更新后",Jc)
        print("----------------------------")
        return [K, w]

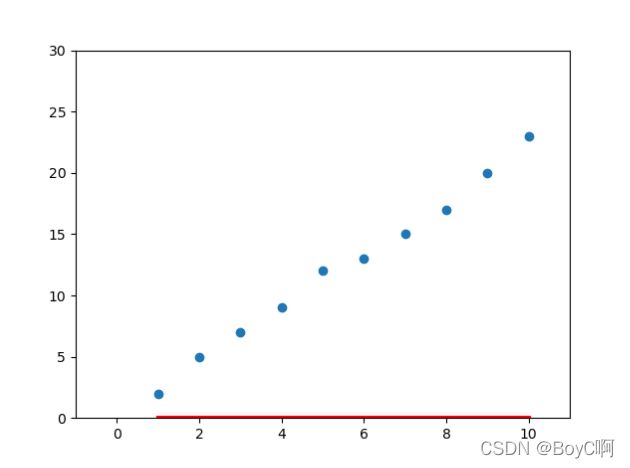
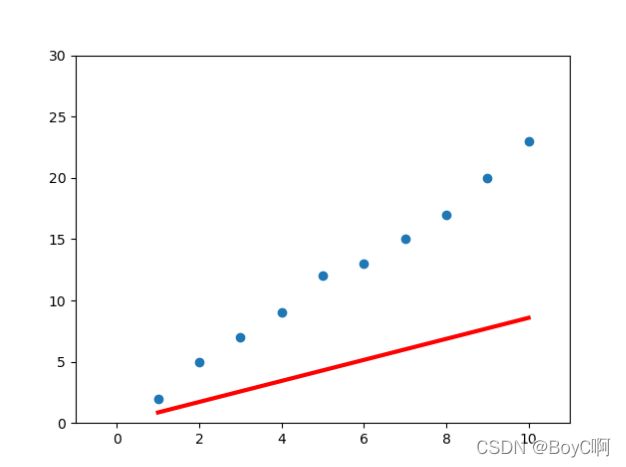
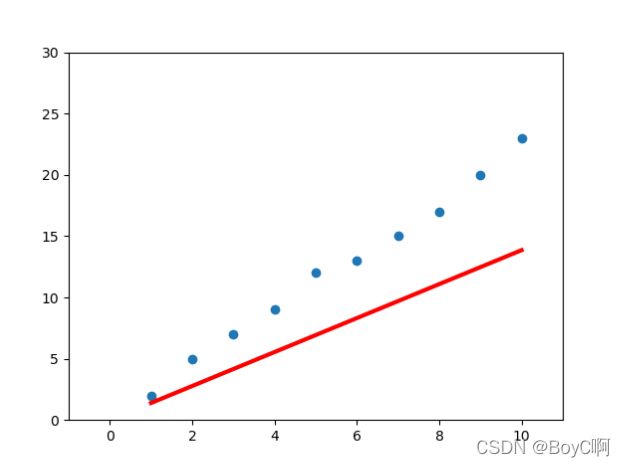
    # 迭代图像
    for i in range(10):

        plt.figure()
        x = np.linspace(1, 10, 100)
        y = x * K
        plt.xlim(-1, 11)
        plt.ylim(0, 30)
        plt.scatter(X_train,Y_train)
        plt.plot(x, y,lw = 3,color = "red")

        #实际更新
        K,W = update(K,W)

        plt.show()

这里就是模拟一下梯度下降的过程！

结果

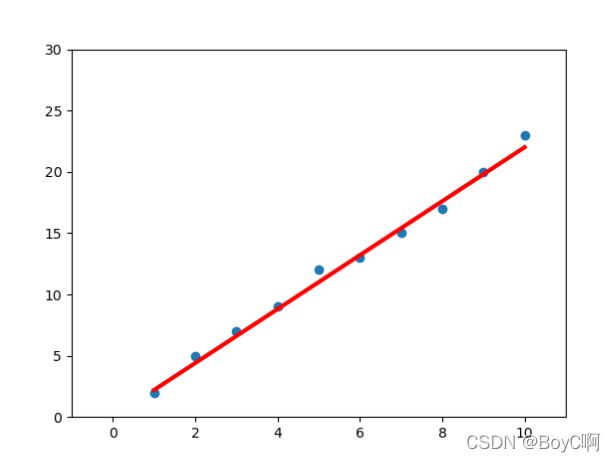
这里图片就不多给，最后得到的图就是

可以看到，10次后就可以拟合一根这样的直线出来！这就是梯度下降的基本思想！至于数学引理，数学推导！咳咳咳，有待提高！

总结

这里也就是浅谈一下梯度下降！至于后面的梯度下降深入，还是路漫漫其修远兮！任重而道远！

记录与 2022 04 14