【darknet源码解析-06】gemm.h和gemm.c解析
本系列为darknet源码解析,本次解析src/gemm.h 与src/gemm.c两个。在上一篇文章中,我们已经详细讲解了输入特征图如何进行转换,那么在本文中,gemm主要完成矢量和矩阵的加速运算,是darknet卷积底层实现的核心,其实也是caffe卷积实现的核心。
gemm.h 的包含的代码如下:主要就是两个函数的gemm,gemm_cpu的定义【gemm_bin暂不分析】,在这里我们先不涉及gpu那块,先讲解cpu这块的矩阵加速运算。
#ifndef GEMM_H
#define GEMM_H
void gemm_bin(int M, int N, int K, float ALPHA,
char *A, int lda,
float *B, int ldb,
float *C, int ldc);
void gemm(int TA, int TB, int M, int N, int K, float ALPHA,
float *A, int lda,
float *B, int ldb,
float BETA,
float *C, int ldc);
void gemm_cpu(int TA, int TB, int M, int N, int K, float ALPHA,
float *A, int lda,
float *B, int ldb,
float BETA,
float *C, int ldc);
#ifdef GPU
void gemm_gpu(int TA, int TB, int M, int N, int K, float ALPHA,
float *A_gpu, int lda,
float *B_gpu, int ldb,
float BETA,
float *C_gpu, int ldc);
void gemm_gpu(int TA, int TB, int M, int N, int K, float ALPHA,
float *A, int lda,
float *B, int ldb,
float BETA,
float *C, int ldc);
#endif
#endifgemm.c 的详细分析如下,可以先看后面的白话总结描述以及小例子再来看源码:
#include "gemm.h"
#include "utils.h"
#include "cuda.h"
#include
#include
#include
void gemm_bin(int M, int N, int K, float ALPHA,
char *A, int lda,
float *B, int ldb,
float *C, int ldc)
{
int i,j,k;
for(i = 0; i < M; ++i){
for(k = 0; k < K; ++k){
char A_PART = A[i*lda+k];
if(A_PART){
for(j = 0; j < N; ++j){
C[i*ldc+j] += B[k*ldb+j];
}
} else {
for(j = 0; j < N; ++j){
C[i*ldc+j] -= B[k*ldb+j];
}
}
}
}
}
float *random_matrix(int rows, int cols)
{
int i;
float *m = calloc(rows*cols, sizeof(float));
for(i = 0; i < rows*cols; ++i){
m[i] = (float)rand()/RAND_MAX;
}
return m;
}
void time_random_matrix(int TA, int TB, int m, int k, int n)
{
float *a;
if(!TA) a = random_matrix(m,k);
else a = random_matrix(k,m);
int lda = (!TA)?k:m;
float *b;
if(!TB) b = random_matrix(k,n);
else b = random_matrix(n,k);
int ldb = (!TB)?n:k;
float *c = random_matrix(m,n);
int i;
clock_t start = clock(), end;
for(i = 0; i<10; ++i){
gemm_cpu(TA,TB,m,n,k,1,a,lda,b,ldb,1,c,n);
}
end = clock();
printf("Matrix Multiplication %dx%d * %dx%d, TA=%d, TB=%d: %lf ms\n",m,k,k,n, TA, TB, (float)(end-start)/CLOCKS_PER_SEC);
free(a);
free(b);
free(c);
}
/**
* gemm函数调用了gemm_cpu()函数,并且将参数原封不动的传给gemm_cpu()
*/
void gemm(int TA, int TB, int M, int N, int K, float ALPHA,
float *A, int lda,
float *B, int ldb,
float BETA,
float *C, int ldc)
{
gemm_cpu( TA, TB, M, N, K, ALPHA,A,lda, B, ldb,BETA,C,ldc);
}
/**
* 被gemm_cpu函数调用,实际完成 C = ALPHA * A * B + C 矩阵运算,输出的C也是按行存储(所有行并成一行)
* @param M A,C的行数(不做转置)
* @param N B,C的列数(不做装置)
* @param K A的列数,C的行数(不做转置)
* @param ALPHA 系数
* @param A 输入矩阵(一维数组格式)
* @param lda A的列数(不做转置)
* @param B 输入矩阵(一维数组格式)
* @param ldb B的列数(不做转置)
* @param C 输入矩阵(一维数组格式)
* @param ldc C的列数(不做转置)
*
* 说明:此函数在gemm_cpu()函数中调用,是其中四中情况之一,A不进行转置,B不进行转置
* 函数名gemm_nt()中nt分别表示 not transpose, tranpose
*/
void gemm_nn(int M, int N, int K, float ALPHA,
float *A, int lda,
float *B, int ldb,
float *C, int ldc)
{ // input: 矩阵A[M,K], filter: 矩阵B[K,N], output: 矩阵C[M,N]
int i,j,k;
#pragma omp parallel for
// 大循环:遍历A的每一行,i表示A的第i行,也是C的第i行
for(i = 0; i < M; ++i){
// 中循环:遍历每一行的所有列,k表示A的第k列,同时表示B的第k行
for(k = 0; k < K; ++k){
// 先计算ALPHA * A (A中每一个元素乘以ALPHA)
register float A_PART = ALPHA*A[i*lda+k];
// 内循环:遍历B中所有列,每次大循环完毕,将计算得到A×B一行的结果
// j是B的第j列,也是C的第j列
for(j = 0; j < N; ++j){
// A中第i行k列与B中第k行i列对应相乘,因为一个大循环要计算A×B一行的结果
// 因此,这里用一个内循环,并没有直接乘以B[k*ldb+i]
// 每个内循环完毕,将计算A×B整行的部分结果(A中第i行k列与B所有列第k行所有元素相乘的结果)
C[i*ldc+j] += A_PART*B[k*ldb+j];
}
}
}
}
/**
* 被gemm_cpu()函数调用,实际完成 C = ALPHA * A * B^T + C 矩阵计算
* @param M A,C的行数(不做转置)或者A^T的行数(做转置),此处A未转置,故为A的行数
* @param N B,C的列数(不做转置)或者B^T的列数(做转置),此处B转置,故为B^T的列数
* @param K A的列数(不做转置)或者A^T的列数(做转置),B的行数(不做转置)或者B^T(做转置),此处A未转置,B转置,故为A的列数,B^T的行数
* @param ALPHA 系数
* @param A 输入矩阵
* @param lda A的列数(不做转置)或者A^T的行数(做转置),此处A未转置,故为A的列数
* @param B 输入矩阵
* @param ldb B的列数(不做转置)或者B^T的行数(做转置),此处B转置,故为B^T的行数
* @param C 输入矩阵
* @param ldc 矩阵C的列数
* 说明:此函数在gemm_cpu()函数中调用,是其中四中情况之一,A不进行转置,B转置
* 函数名gemm_nt()中nt分别表示 not transpose, tranpose
*/
void gemm_nt(int M, int N, int K, float ALPHA,
float *A, int lda,
float *B, int ldb,
float *C, int ldc)
{// input: 矩阵A[M,K], filter: 矩阵B[K,N], output: 矩阵C[M,N]
int i,j,k;
#pragma omp parallel for
// 大循环:遍历A的每一行,i表示A的第i行,也是C的第i行
for(i = 0; i < M; ++i){
for(j = 0; j < N; ++j){
register float sum = 0;
//内循环:每次内循环结束,将计算A中第i行与B中第j列相乘的结果
//也就是得到C[i][j],因为C也一维化,且按行存储,所以得到C[i*lda+j]
// k表示A的第几列,也表示
for(k = 0; k < K; ++k){
sum += ALPHA*A[i*lda+k]*B[j*ldb + k];
}
C[i*ldc+j] += sum;
}
}
}
/**
* 被gemm_cpu()函数调用,实际完成 C = ALPHA * A^T * B + C 矩阵计算
* @param M A,C的行数(不做转置)或者A^T的行数(做转置),此处A转置,故为A^T的行数
* @param N B,C的列数(不做转置)或者B^T的列数(做转置),此处B未转置,故为B的列数
* @param K A的列数(不做转置)或者A^T的列数(做转置),B的行数(不做转置)或者B^T行数(做转置),此处A未转置,B转置,故为A^T的列数,B的行数
* @param ALPHA 系数
* @param A 输入矩阵
* @param lda A的列数(不做转置)或者A^T的行数(做转置),此处A转置,故为A^T的行数
* @param B 输入矩阵
* @param ldb B的列数(不做转置)或者B^T的行数(做转置),此处B未转置,故为B的列数
* @param C 输入矩阵
* @param ldc 矩阵C的列数
* 说明:此函数在gemm_cpu()函数中调用,是其中四中情况之一,A进行转置,B不进行转置
* 函数名gemm_tn()中tn分别表示 tranpose,not transpose
*/
void gemm_tn(int M, int N, int K, float ALPHA,
float *A, int lda,
float *B, int ldb,
float *C, int ldc)
{
int i,j,k;
#pragma omp parallel for
for(i = 0; i < M; ++i){
for(k = 0; k < K; ++k){
register float A_PART = ALPHA*A[k*lda+i];
for(j = 0; j < N; ++j){
C[i*ldc+j] += A_PART*B[k*ldb+j];
}
}
}
}
/**
* 被gemm_cpu()函数调用,实际完成 C = ALPHA * A^T * B^T + C 矩阵计算
* @param M A,C的行数(不做转置)或者A^T的行数(做转置),此处A转置,故为A^T的行数
* @param N B,C的列数(不做转置)或者B^T的列数(做转置),此处B转置,故为B^T的列数
* @param K A的列数(不做转置)或者A^T的列数(做转置),B的行数(不做转置)或者B^T(做转置),此处A转置,B转置,故为A^T的列数,B^T的行数
* @param ALPHA 系数
* @param A 输入矩阵
* @param lda A的列数(不做转置)或者A^T的行数(做转置),此处A转置,故为A^T的行数
* @param B 输入矩阵
* @param ldb B的列数(不做转置)或者B^T的行数(做转置),此处B转置,故为B^T的行数
* @param C 输入矩阵
* @param ldc 矩阵C的列数
* 说明:此函数在gemm_cpu()函数中调用,是其中四中情况之一,A进行转置,B进行转置
* 函数名gemm_tt()中tt分别表示 transpose, tranpose
*/
void gemm_tt(int M, int N, int K, float ALPHA,
float *A, int lda,
float *B, int ldb,
float *C, int ldc)
{
int i,j,k;
#pragma omp parallel for
for(i = 0; i < M; ++i){
for(j = 0; j < N; ++j){
register float sum = 0;
for(k = 0; k < K; ++k){
sum += ALPHA*A[i+k*lda]*B[k+j*ldb];
}
C[i*ldc+j] += sum;
}
}
}
/**
* 矩阵计算,完成C = ALPHA * A * B + BETA * C 矩阵计算,最后的输出为C
* @param TA 是否需要对A做转置操作,是为1,否为0(要不要转置取决于A,B之间的维度是否匹配,比如A:3*2, B:4*2, 则需要对B转置,才满足矩阵乘法)
* @param TB 同上
* @param M A,C 的行数(若A需要转置,则此出给出转置后A即A^T的行数,而不是转置前的)
* @param N B,C 的列数(若B需要转置,则此处给出转置后B即B^T的列数,而不是转置前的)
* @param K A的列数,B的行数(同样,若A与B中的二者或者其中一个需要转置,则不管怎么样,转置后的A,B必须行列能够匹配,符合矩阵乘法规则,K也是转置后的值,不是转置的)
* @param ALPHA 系数
* @param A 输入矩阵
* @param lda A的列数(不做转置)或者行数(做转置,且给的是转置后A即A^T的行数)
* @param B 输入矩阵
* @param ldb B的列数(不做转置)或者行数(做转置,且给的是转置后B即B^T的行数)
* @param BETA 系数
* @param C 输入矩阵
* @param ldc C的列数
*/
void gemm_cpu(int TA, int TB, int M, int N, int K, float ALPHA,
float *A, int lda,
float *B, int ldb,
float BETA,
float *C, int ldc)
{
//printf("cpu: %d %d %d %d %d %f %d %d %f %d\n",TA, TB, M, N, K, ALPHA, lda, ldb, BETA, ldc);
int i, j;
// 先行计算BETA * C,并把结果存入C中,得到C将为M行N列(按行存储在一维数组中)
for(i = 0; i < M; ++i){
for(j = 0; j < N; ++j){
C[i*ldc + j] *= BETA;
}
}
if(!TA && !TB) // TA = 0, TB = 0,
gemm_nn(M, N, K, ALPHA,A,lda, B, ldb,C,ldc);
else if(TA && !TB) // TA = 1, TB = 0
gemm_tn(M, N, K, ALPHA,A,lda, B, ldb,C,ldc);
else if(!TA && TB) // TA = 0, TB = 1
gemm_nt(M, N, K, ALPHA,A,lda, B, ldb,C,ldc);
else // TA = 1, TB = 1
gemm_tt(M, N, K, ALPHA,A,lda, B, ldb,C,ldc);
}
#ifdef GPU
#include
/**
* 矩阵计算GPU实现,调用CUDA中cublasSgemm()函数完成 C_gpu = ALPHA + A_gpu * B_gpu + BETA * C_gpu的线性矩阵运算,
* 与gemm_cpu()基本类似,输入参数也基本相同,但是存在两点不同:
* 1. 此处是直接调用CUDA cuBLAS库中的cublasSgemm()函数进行矩阵运算,而无需gemm_cpu()那样,需要自己用循环挨个元素相乘实现;
* 2. 在GPU中,默认采用的矩阵存储格式是按列存储,而不是我们之前一度习惯的按行存储,此处调用的cublasSgemm()也不例外,
* 所以下面会有一些不同的操作(由于这个原因,相比于cpu版本的gemm_cpu(),又要复杂一些)
*
*
*
*
* GPU使用cuBLAS库中cublasSgemm()函数进行矩阵乘法计算,参看:
* 这个网址是CUDA关于cuBLAS库的官方文档,此处cublasSgemm()函数在2.7.1节: cublasgemm();
* 可以看出cublasSgem()函数完成C_gpu = ALPHA * A_gpu * B_gpu + BETA * C_gpu的线性矩阵计算
*
* @param TA 是否需要对A做转置操作,是为1,否为0(要不要转置取决于A,B之间的维度是否匹配,比如A:3*2, B:4*2, 则需要对B转置,才满足矩阵乘法)
* @param TB 同上
* @param M A,C 的行数(若A需要转置,则此出给出转置后A即A^T的行数,而不是转置前的)
* @param N B,C 的列数(若B需要转置,则此处给出转置后B即B^T的列数,而不是转置前的)
* @param K A的列数,B的行数(同样,若A与B中的二者或者其中一个需要转置,则不管怎么样,转置后的A,B必须行列能够匹配,符合矩阵乘法规则,K也是转置后的值,不是转置的)
* @param ALPHA 系数
* @param A_gpu 输入矩阵,且其内存在GPU设备内存中,不在主机内存中(由cudaMalloc分配,由cudaFree释放)
* @param lda A的列数(不做转置)或者行数(做转置,且给的是转置后A即A^T的行数)
* @param B_gpu 输入矩阵,且其内存在GPU设备内存中,不在主机内存中(由cudaMalloc分配,由cudaFree释放)
* @param ldb B的列数(不做转置)或者行数(做转置,且给的是转置后B即B^T的行数)
* @param BETA 系数
* @param C_gpu 输入矩阵,且其内存在GPU设备内存中,不在主机内存中(由cudaMalloc分配,由cudaFree释放)
* @param ldc C的列数
*
* 可以看出,如果不是因为存储方式的不同,cublasSgemm()函数的结构也与darknet自己实现的cpu版本的gemm_cpu一模一样;
* 因为二者存储格式不同,需要交换A_gpu, B_gpu的位置,对应M和N之间,TB与TA之间,ldb与lda之间都要相互交换;
*
*/
void gemm_gpu(int TA, int TB, int M, int N, int K, float ALPHA,
float *A_gpu, int lda,
float *B_gpu, int ldb,
float BETA,
float *C_gpu, int ldc)
{
//根据官网,这个变量是一个对开发者不透明的变量,也就是里面聚义包给什么,开发这一般无法知道,
//只知道里面包含的cuBLAS库的相关信息,且这个变量是必须的,按照官网的描述,CUBLAS库中所有的函数都需要这个变量参数
//(且都是作为第一个参数),该变量由cublasCreate()初始化,并由cuBLASDestroy()销毁。
cublasHandle_t handle = blas_handle();
/* cublasSgemm()函数输入参数说明
* @param handle
* @param transa 是否需要转置A_gpu, 这里transa = TB ? CUBLAS_OP_T : CUBLAS_OP_N (是个条件表达式),如果TB =1,
* 则取CUBLAS_OP_T,即需要对A_gpu转置;
* @param transb 是否需要转置A_gpu, 这里transa = TA ? CUBLAS_OP_T : CUBLAS_OP_N (是个条件表达式),如果TA =1,
* 则取CUBLAS_OP_T,即需要对B_gpu转置;
* @param M A_gpu,C_gpu 的行数(若A_gpu需要转置,则此出给出转置后A_gpu即A_gpu^T的行数,而不是转置前的)
* @param N B_gpu,C_gpu 的列数(若B_gpu需要转置,则此处给出转置后B_gpu即B_gpu^T的列数,而不是转置前的)
* @param K A_gpu的列数,B_gpu的行数(同样,若A_gpu与B_gpu中的二者或者其中一个需要转置,则不管怎么样,转置后的A_gpu,B_gpu必须
* 行列能够匹配,符合矩阵乘法规则,K也是转置后的值,不是转置的)
* @param ALPHA 实数系数
* @param B_gpu 输入矩阵
* @param ldb B_gpu的列数(不做转置)或者行数(做转置,且传入的是转置后B_gpu即B_gpu^T的行数)
* @param A_gpu 输入矩阵
* @param lda A_gpu的列数(不做转置)或者行数(做转置,且传入的是转置后A_gpu即A_gpu^T的行数)
* @param BETA 实数系数
* @param C_gpu 计算结果
* @param ldc C_gpu的列数
*
*/
cudaError_t status = cublasSgemm(handle, (TB ? CUBLAS_OP_T : CUBLAS_OP_N),
(TA ? CUBLAS_OP_T : CUBLAS_OP_N), N, M, K, &ALPHA, B_gpu, ldb, A_gpu, lda, &BETA, C_gpu, ldc);
// 检查cublasSgemm运算是否正常
check_error(status);
}
#include
#include
#include
#include
void time_gpu_random_matrix(int TA, int TB, int m, int k, int n)
{
float *a;
if(!TA) a = random_matrix(m,k);
else a = random_matrix(k,m);
int lda = (!TA)?k:m;
float *b;
if(!TB) b = random_matrix(k,n);
else b = random_matrix(n,k);
int ldb = (!TB)?n:k;
float *c = random_matrix(m,n);
int i;
clock_t start = clock(), end;
for(i = 0; i<32; ++i){
gemm_gpu(TA,TB,m,n,k,1,a,lda,b,ldb,1,c,n);
}
end = clock();
printf("Matrix Multiplication %dx%d * %dx%d, TA=%d, TB=%d: %lf s\n",m,k,k,n, TA, TB, (float)(end-start)/CLOCKS_PER_SEC);
free(a);
free(b);
free(c);
}
void time_gpu(int TA, int TB, int m, int k, int n)
{
int iter = 10;
float *a = random_matrix(m,k);
float *b = random_matrix(k,n);
int lda = (!TA)?k:m;
int ldb = (!TB)?n:k;
float *c = random_matrix(m,n);
float *a_cl = cuda_make_array(a, m*k);
float *b_cl = cuda_make_array(b, k*n);
float *c_cl = cuda_make_array(c, m*n);
int i;
clock_t start = clock(), end;
for(i = 0; i 其实,gemm总结起来就完成一个矩阵乘法的运算:C = ALPHA * A * B + BETA * C
上述公式中,A,B,C为矩阵,A,B为输入矩阵,C矩阵保存运算结果。ALPHA,BETA为系数。这样看起来是不是很简单,接下来我们需要考虑矩阵A,B的行数和列数分别是多少,这里我们假设矩阵A为[M,K],矩阵B为[K,N],那么矩阵C为[M,N]。我们都直到矩阵A,B,C在逻辑是一个二维的结果,在这里实际的存储结构是一个一维数组,按行存储。
接下来,我们来具体看一个例子,为了方便运算,我们这里假设ALPHA=1,BETA=0。实际上我们只对A*B进行运算,我们分为四种情况进行讨论,为什么要分为四种情况呢?其实就是引入矩阵的转置。
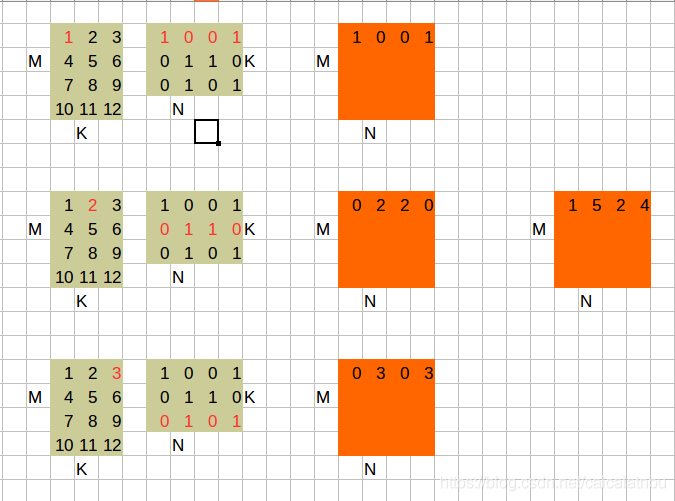
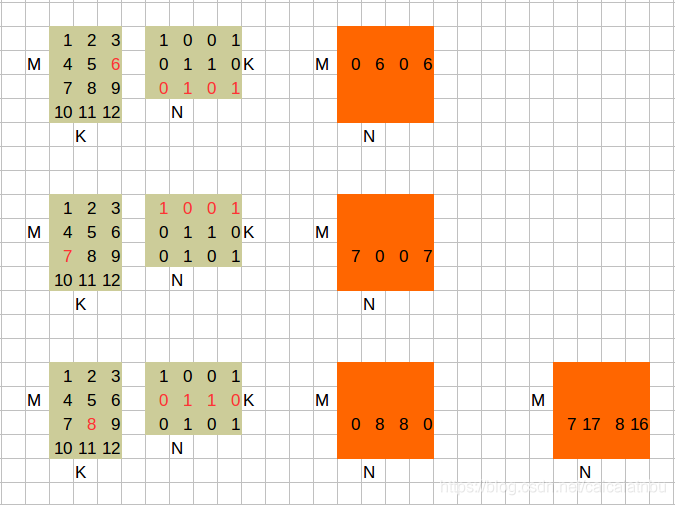
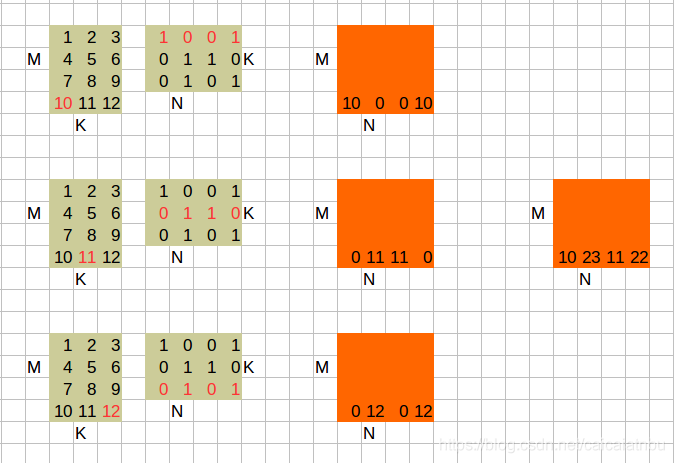
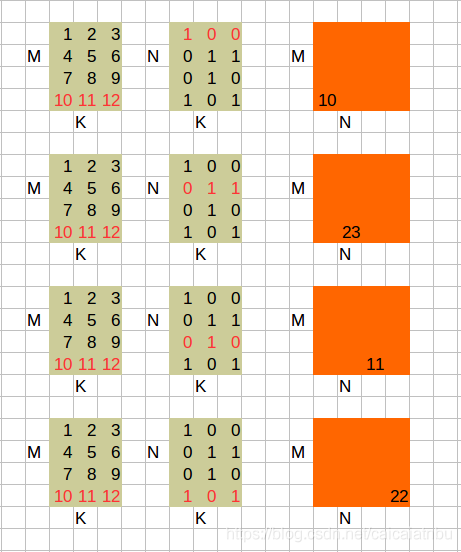
1. A * B
综合计算一下,矩阵C的内容如下:
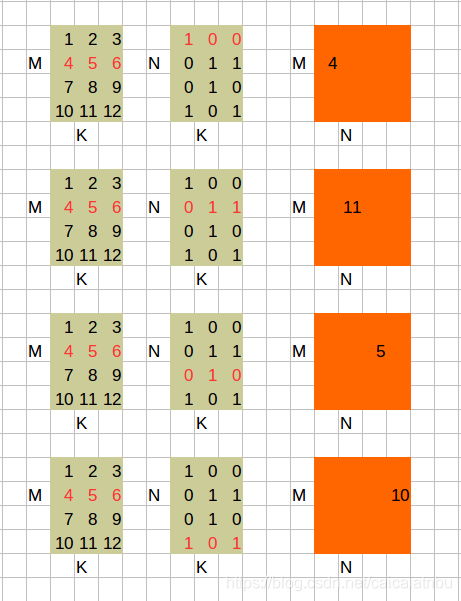
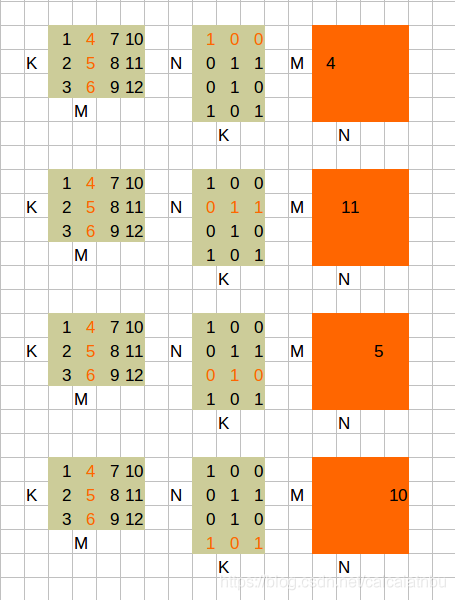
2. A^T * B
其实这跟A* B h很想象。
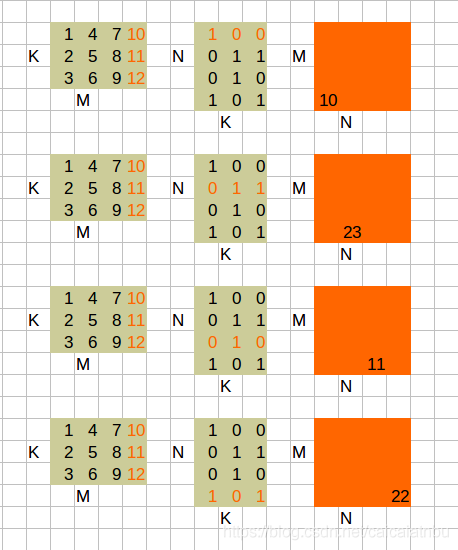
3. A * B^T
综合一下,便可以得到结果
4 A^T * B^T
跟A * B^T很想象。
ok,此时你再取看源码豁然开朗。
gemm_nn 函数就是计算 A * B这种类型;
gemm_tn 函数就是计算A^T * B这种类型;
gemm_nt 函数就是计算A * B^T这种类型;
gemm_tt 函数就是计算A^T * B^T 这种类型;
gemm_cpu 函数就是根据矩阵A和B的情况来实际调用 gemm_nn 、gemm_tn 、gemm_nt、gemm_tt 函数;
gemm 函数其实就是在gemm_cpu函数上再封装一层,参数原封不动传递给gemm_cpu函数;
完,