深度学习（matlab）学习笔记——1.单层神经网络

       单层神经网络通过一个输入层计算后得到输出层，对每个输入通过加权求和（w），以及加阈值（b），再通过激活函数f（x）得到对应的输出。

       在监督学习下输入的数据为 [输入，正确输入] ,即已经获得了正确的结果，在训练过程中通过已知的数据集来训练参数w，在训练过程中有采用增量规则，具体有两种算法随机梯度下降法（SGD）以及批量算法（Batch），其中SGD速度更快，Batch对数据要求不大，稳定性好。

一、随机梯度下降算法

采用Sigmoid作为激活函数，w=w+alpha*y'(v)*e*x（Latex还没学，学会了回来改公式五五-）作为增量规则，代码如下：

 

%随机梯度下降算法
% 采用Sigmoid作为激活函数
% 用式w=w+alpha*y'(v)*e*x作为增量规则
% w为权重，alpha为学习因子（0，1）
% v=wx+b
% y为激活函数y = 1/(1+exp(-x))
% y’为当前状态激活函数导数
% Sigmoid导数为y’=y*（1-y）
% e为输出节点误差e=d-y（d为监督学习的正确结果）
% x为节点输入 
function W = DeltaSGD(W,X,D)
    alpha = 0.9;
    N = 4;%数据量N组
    for k = 1:N
        x = X(k,:)';
        d = D(k);
        v = W*x;
        y = Sigmoid(v);
        e = d-y;
        delta = y*(1-y)*e;
        dW = alpha*delta*x;
        
        %更新W
        W(1) = W(1)+dW(1);
        W(2) = W(2)+dW(2);
        W(3) = W(3)+dW(3);
    end
end

我没有使用matlab自带的Sigmoid函数，那个需要自己来调整输入格式，所以我们写一个sigmoid函数：

function y = Sigmoid(x)
    y = 1/(1+exp(-x));
end

然后我们来测试一下，对于这样的一个输入矩阵：

0	0	1	0
0	1	1	0
1	0	1	1
1	1	1	1

加粗列为正确结果，前面三列为输入

clear all
X = [0 0 1;
     0 1 1;
     1 0 1;
     1 1 1;];
D = [0
     0    
     1 
     1];
W = 2*rand(1,3)-1;
for epoch = 1:10000
    W = DeltaSGD(W,X,D);
end
N = 4;
for k = 1:N
    x = X(k,:)';
    v = W*x;
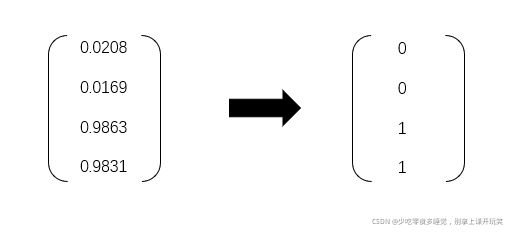
    y = Sigmoid(v)
end

得到结果为

 二、批量算法

使用整个训练集的优化算法被称为批量（batch）或确定性（deterministic）算法，因为它们会在一个大批量中同时处理所有样本。（公式等我学一下。。。）简单来讲就是w=（1/N）Σw

直接上代码吧：

%批量算法
%增量规则：w=1/N（Σ（1-N）w（k））
function W = DeltaBatch(W,X,D)
    alpha = 0.9;
    dWsum = zeros(3,1);
    N = 4;
    for k = 1:N
        x = X(k,:)';
        d = D(k);
        v = W*x;
        y = Sigmoid(v);
        e = d-y;
        delta = y*(1-y)*e;
        dW = alpha*delta*x;
        dWsum = dWsum + dW;
    end
    dWavg = dWsum/N;
    W(1) = W(1)+dWavg(1);
    W(2) = W(2)+dWavg(2);
    W(3) = W(3)+dWavg(3);
end

测试一下，这里想要让批量算法训练速度较慢,所以误差较SGD来讲较大,后面会有两种算法的比较：
 

clear all
X = [0 0 1;
     0 1 1;
     1 0 1;
     1 1 1;];
D = [0
     0  
     1 
     1];
W = 2*rand(1,3)-1;
for epoch = 1:10000
    W = DeltaBatch(W,X,D);
end
N = 4;
for k = 1:N
    x = X(k,:)';
    v = W*x;
    y = Sigmoid(v)
end

结果:

 三、两种算法运行比较

将两种算法放在一起,设定相同的初始权重,比较二者每轮的与真实值误差,我们可以根据最后得到的结果看出两种算法调整权重的快慢:

clear all
X = [0 0 1;
     0 1 1;
     1 0 1;
     1 1 1;];
D = [0
     0  
     1 
     1];
E1 = zeros(1000,1);
E2 = E1;
%平均误差

%让二者有相同的初始权重，控制变量
W1 = 2*rand(1,3)-1;
W2 = W1;

for epoch = 1:1000
    W1 = DeltaSGD(W1,X,D);
    W2 = DeltaBatch(W2,X,D);
    
    %误差
    es1 = 0;
    es2 = 0;

    N = 4;
    for k = 1:N
        x = X(k,:)';
        d = D(k);
        
        v1 = W1*x;
        y1 = Sigmoid(v1);
        es1 = es1+(d-y1)^2;
    
        v2 = W2*x;
        y2 = Sigmoid(v2);
        es2 = es2+(d-y2)^2;
    end
    E1(epoch) = es1/N;
    E2(epoch) = es2/N;
end
plot(E1,'r')
hold on 
plot(E2,'b:')
xlabel('epoch')
ylabel('Average of Training error')
legend('SGD','Batch')

结果:

 可以看出SGD的调整速度更快.

四、单层神经网络的局限性

简单来讲就是只能进行线性的划分,无法对非线性因素导致的变化产生影响,所以多层的神经网络的一个作用就是拓展维度,增加非线性因素(复习一下无人驾驶!_!)

这个图的效果比较明显,帮助理解:

这是我们上面例子中用到的矩阵,可以认为前面两列是坐标,第四列正确结果是四个点中的两个类别,我们通过单层神经网络可以找到如图所示的这样一条直线来将两类点进行划分,但是我们改变一下呢?

 

当我们的输入数据变成这样,改变了点的分布,我们就需要这样一条非线性的曲线来进行分类,那么我们上面构建的单层神经网络无法实现了 ,我们可以接着用之前的模型来检验一下这组输入: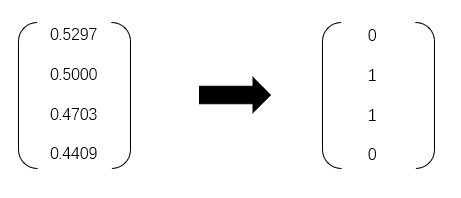

这就是我们辛苦训练了1个w的模型,根本傻傻分不清,所以使用单层神经网络是无法实现这样的非线性划分的,我们就需要来拓展神经网络的隐藏层,学习后面的多层神经网络.