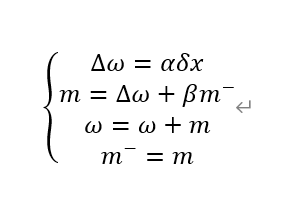深度学习(matlab)学习笔记——2.多层神经网络
2.1反向传播算法(Backprop)
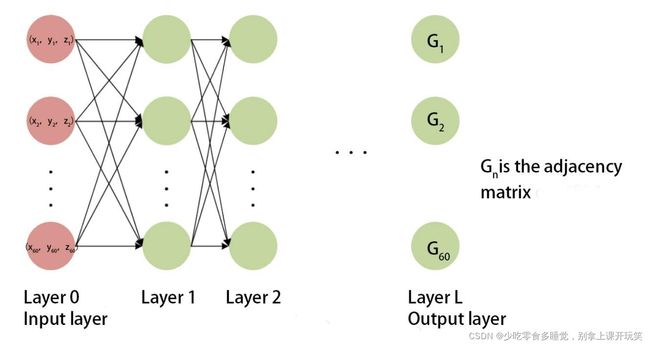
根据上一章最后得到的结果我们可以发现,单层的神经网络尽管节点再多也不能解决非线性分类问题(还有其他很多问题),所以我们需要如下图所示的多层神经网络(感谢数模队友做的图~~)
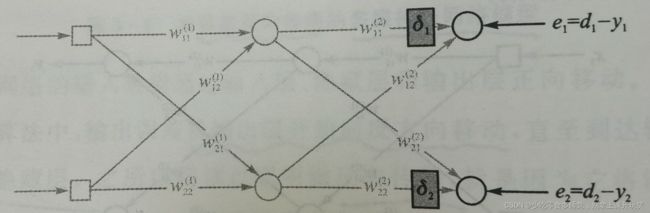
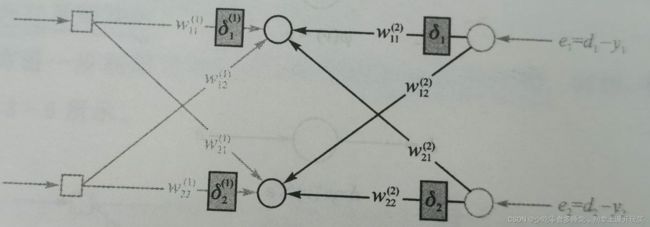
显然,当隐含层数增多,我们就无法通过正确输入的结果与计算结果计算误差从前往后进行修正权重,因为我们并不知道第一隐含层的正确结果,所以,就可以转换思维,从后往前,从输出层反向推导,之后再用计算出的误差向前与权重相乘,最后直到将这个误差经过多层网络加权逆推回到输入,这样这个最终的误差就与上一章的增量规则相同,进行相同的修正即可。
多层神经网络反向传播中重点在于将误差反向逆推,整体上最后也相当于是正确答案与计算结果之间的误差,只是经过多个隐含层,进行了多次加权求和运算。
具体过程如图所示,改图来自于[韩]Phil Kim博士的《深度学习:基于MATLAB的设计实例》(我就是按这本书自学的,还是很基础,很适合新手入门的)
我们利用反向传播解决了权重无法计算的问题后,剩下的无非是多计算一次隐含层权重罢了,那就按照之前的思路,实现之前不能解决的XOR问题。
function [W1,W2] = BackpropXOR(W1,W2,X,D)
alpha = 0.9;%学习因子
N = 4;
for k = 1:N
x = X(k,:)';
d = D(k);
v1 = W1*x;
y1 = Sigmoid(v1);%隐藏层结果即输出层输入
v = W2*y1;
y = Sigmoid(v);
e = d-y;
delta = y.*(1-y).*e;%输出层误差
e1 = W2'*delta;
delta1 = y1.*(1-y1).*e1;%反向传播,隐藏层误差
dW1 = alpha*delta1*x';
W1 = W1+dW1;%更新输入层——隐藏层权重
dW2 = alpha*delta*y1';
W2 = W2+dW2;%更新隐藏层——输出层权重
end
endMATLAB中(.*)和(*)的区别不用讲了吧,记得改Sigmoid噻!
下面是测试程序
clc;clear all
X = [0 0 1;
0 1 1;
1 0 1;
1 1 1;];
D = [0
1
1
0];
W1 = 2*rand(4,3)-1;
W2 = 2*rand(1,4)-1;
for epoch = 1:10000
[W1,W2] = BackpropXOR(W1,W2,X,D);
end
N = 4;
for k = 1:N
x = X(k,:)';
v1 = W1*x;
y1 = Sigmoid(v1);
v = W2*y1;
y = Sigmoid(v)
end
这章有点长,忍一下,结果就不贴了,与之前得到的分类结果类似。
2.2 动量法(Momentum)
首先,动量法是一种权重调整的变化形式,我们把一个动量mmt加入到增量规则中进行调整权重,他会向一个方向推动权重调整,但不是马上发生变化,作用类似物理学的动量,能阻碍物体对外力的快速反应。(书上原话~~)
利用动量法来修正权重的公式为(β是0到1之间调整因子)
其中,我们试着推导m(3)(还是没学Latex,word点出来公式,凑活看~~)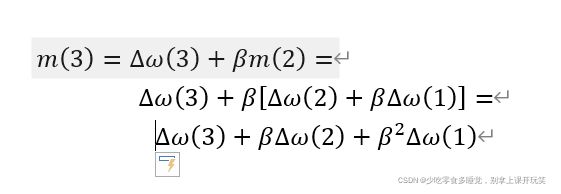
所以,我的理解是,之前每次的调整量会对之后的调整产生影响,而越接近的调整带来的影响越大,越“远”的调整带来的影响越小。(可以联想到时间序列模型~~)。总之,这种方法保留之前的权重更新,有稳定性,同时,随着更新次数累计,动量越来越大,更新量越来越大,学习速度得到了提升。
function [W1,W2] = BackpropMmt(W1,W2,X,D)
alpha = 0.9;%学习因子
beta = 0.9;%动量调整因子
%mmt为动量,与每次权重更新值有关,参考时间序列模型&差分方程模型
%导致每次的权重调整量受最近这次的调整量影响最大,越靠前影响越小
%mmt递增,学习速度逐渐加快,并且受之前所有轮的影响,有稳定性
mmt1 = zeros(size(W1));
mmt2 = zeros(size(W2));
N = 4;
for k = 1:N
x = X(k,:)';
d = D(k);
v1 = W1*x;
y1 = Sigmoid(v1);%隐藏层的输出,即输出层的输入
v = W2*y1;
y = Sigmoid(v);%输出层结果
e = d-y;
delta = y.*(1-y).*e;%输出层误差
e1 = W2'*delta;
delta1 = y1.*(1-y1).*e1;%反向传播,隐藏层误差
dW1 = alpha*delta1*x';
mmt1 = dW1+beta*mmt1;%动量法关键,mmt计算方法
W1 = W1+mmt1;
dW2 = alpha*delta*y1';
mmt2 = dW2+beta*mmt2;
W2 = W2+mmt2;
end
endtest的话换个函数名就行了,效果不好就自己多循环几遍,相信你们搞得定。
2.3 代价函数
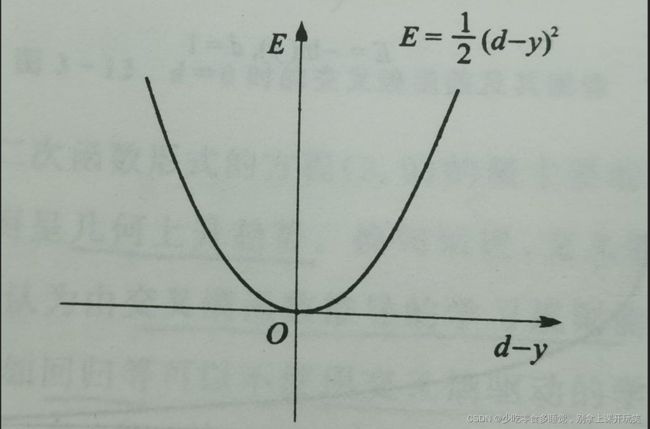
对神经网络误差的测量方法就是代价函数,一个好的代价函数选择应该要让误差越大,代价函数值越大,一般有两种代价函数
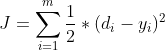 (1)
(1)
![J=\sum_{i=1}^{m}[-d_{i}ln(y_{i})-(1-d_{i})ln(1-y_{i})]](http://img.e-com-net.com/image/info8/0b94eff2bab94ef0bb42ef0cb95dfe4f.gif) (2)
(2)
其中,我们前面采用的都是这类误差平方函数,即公式(1)
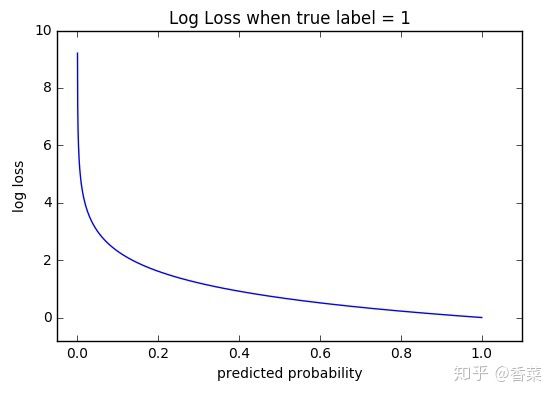
而更广泛与Sigmoid和Softmax写作使用的公式(2)为交叉熵函数
如图所示,当label为1时,靠近1的损失函数值为0,远离1,损失函数值增大,呈指数式增长,这样可以有效进行分类,对误差更加敏感。
function [W1,W2] = BackpropCE(W1,W2,X,D)
alpha = 0.9;%学习因子
N = 4;
for k = 1:N
x = X(k,:)';
d = D(k);
v1 = W1*x;
y1 = Sigmoid(v1);%隐藏层结果即输出层输入
v = W2*y1;
y = Sigmoid(v);
e = d-y;
delta = e;%输出层误差
%该处为采用交叉熵与普通反传播区别,效率更高
e1 = W2'*delta;
delta1 = y1.*(1-y1).*e1;%反向传播,隐藏层误差
dW1 = alpha*delta1*x';
W1 = W1+dW1;%更新输入层——隐藏层权重
dW2 = alpha*delta*y1';
W2 = W2+dW2;%更新隐藏层——输出层权重
end
end同样测试文件直接更改函数名即可。
下面,我们对两种函数进行比较:
clc;clear all
X = [0 0 1;
0 1 1;
1 0 1;
1 1 1;];
D = [1
0
0
1];
E1 = zeros(1000,1);
E2 = zeros(1000,1);
W11 = 2*rand(4,3)-1;
W12 = 2*rand(1,4)-1;
W21 = W11;
W22 = W12;
%控制变量,初始权重相同
for epoch = 1:1000
[W11,W12] = BackpropCE(W11,W12,X,D);
[W21,W22] = BackpropXOR(W21,W22,X,D);
es1 = 0;
es2 = 0;%误差平方和
N = 4;
for k = 1:N
x = X(k,:)';
d = D(k);
v1 = W11*x;
y1 = Sigmoid(v1);
v = W12*y1;
y = Sigmoid(v);
es1 = es1+(d-y)^2;
v1 = W21*x;
y1 = Sigmoid(v1);
v = W22*y1;
y = Sigmoid(v);
es2 = es2+(d-y)^2;
end
E1(epoch) = es1/N;
E2(epoch) = es2/N;
end
plot(E1,'r')
hold on
plot(E2,'b:')
xlabel('轮数')
ylabel('训练误差平均值')
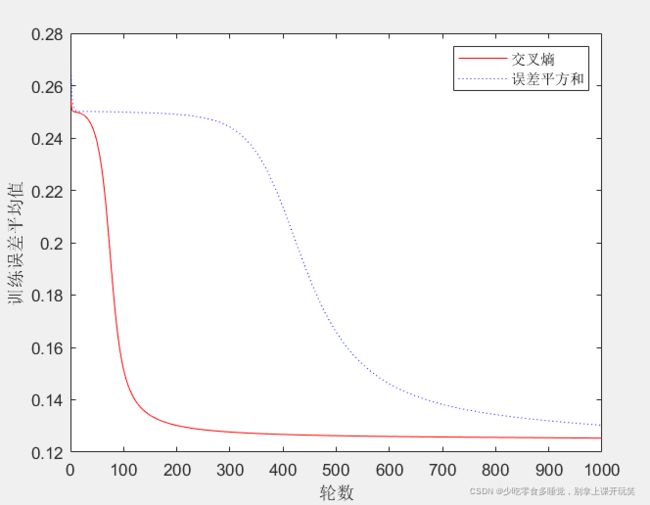
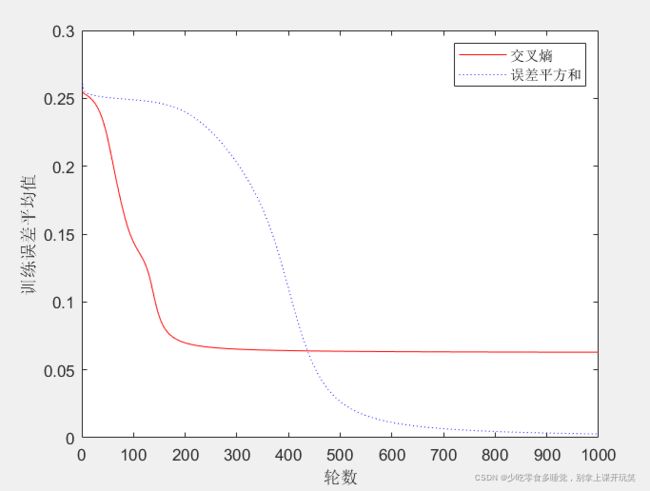
legend('交叉熵','误差平方和')结果如图所示:
由交叉熵驱动的训练降低误差速度更快,有一个更快的学习过程,所以大多数深度学习的代价函数采用交叉熵函数。(当然在实际运行时也会产生如下结果,采用交叉熵可能会导致误差不收敛,困在某一个地方,这个我暂时也没有搞懂,但是绝大多数情况下交叉熵函数都是很好用的!!)
另外,也可以将动量法与两种代价函数结合,基本上会有更好的效果。但时根据实际数据的不同会有一定的偏差,但是增大实验量可以减少这种情况。