2022电赛F题思路

2022电赛到现在为止已经出了结果。这是我第一次参加电赛，以前也没有相关的比赛经历，在这四天三夜的时间里能够和队友完成这样一项完整的作品，对我们来说都具有很大的意义。虽然最后还是有一些细节上的问题，不过我们对结果都很满意。在这里分享一下我们的解法思路，希望能够帮助到有需要的朋友们。

一、任务

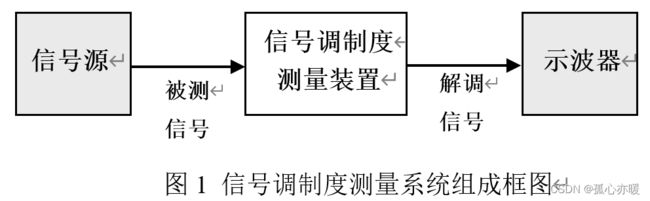
设计制作信号调制度测量装置，该装置测量并显示信号源输出的被测信号调制度等参数，识别并显示被测信号的调制方式，输出解调信号。测量系统如图1所示。

二、要求

（1）被测信号为电压峰峰值100mV的普通单音调幅（AM）电压$U_{AM}$，其载频为10MHz、调制信号为频率1~3kHz的正弦信号。测量并显示的$U_{AM}$调幅度$m_a$，要求测量误差绝对值|$\Delta$|≤0.1；输出解调信号，要求解调信号波形无明显失真。 （20分）

（2）被测信号为电压峰峰值100mV的单音调频（FM）电压$U_{FM}$，其载频为10MHz、调制信号为频率3~5kHz的正弦信号。测量并显示的$U_{FM}$调频度$m_f$，测量误差绝对值|$\Delta$|≤0.3；测量并显示的最大$U_{FM}$频偏|$\Delta$$f_m$|(kHz)；输出解调信号，要求解调信号波形无明显失真。（25分）

（3）被测信号为载波电压峰峰值100mV的高频电压$U_m$，其载频范围为10MHz~30MHz（频率步进间隔0.5MHz）。若为$U_m$为已调波（AM或FM波）时，其调制信号为频率范围5kHz~10kHz（频率步进间隔1kHz）内某一频率的正弦信号。测量装置应能自主识别的$U_m$调制方式，即能判断出$U_m$为调幅、调频或未调载波。测量并显示$U_m$的调制度（$m_a$或$m_f$），测量误差要求分别同前面第(1)、(2)项的要求；当被测信号为调频波时，要求测量并显示其最大频偏|$\Delta$$f_m$|(kHz)；输出解调信号，要求解调信号波形无明显失真。（45分）

（4）其他（10分）

（5）设计报告（20分）

项 目	主要内容	满分
方案论证	比较与选择，方案描述。	3
理论分析与计算	系统相关参数设计	5
电路与程序设计	系统组成，原理框图与各部分电路图，系统软件与流程图。	5
测试方案与测试结果	测试结果完整性，测试结果分析。	5
设计报告结构及规范性	摘要，正文结构规范，图表的完整与准确性。	2
总分	20

三、说明

（1）题中“普通单音调幅波”是指：载波为正弦波，调制信号为单频正弦信号，其频谱包括完整的载频与上、下边频分量。题中“单音调频波”是指：载波为正弦波，调制信号为单频正弦信号。

（2）本题被测信号为AM信号时，其调幅度范围是：0.2＜$m_a$≤1；被测信号为FM信号时，其调频度范围是：1≤$m_f$≤6；被测信号为未调载波，是指被测信号为正弦载波或连续波（CW）。本题第（3）项要求测量装置能自主识别出被测信号的三种可能调制方式。

（3）如测量装置需对被测信号进行A/D变换，应借鉴适用于对高频窄带信号抽样的“带通抽样定律”。“奈奎斯特抽样定律”亦称为“低通抽样定律”，它适于对基带信号的抽样。

（4）测试时可自带具有AM/FM调制信号输出功能的信号源，并以自带信号源输出信号的参数设置值作为测量基准值。

（5）要求第（3）项的操作必须是一键启动，装置应连续完成调制方式识别与调制度等参数的测量和显示，测量过程中不得有人工介入。

解法思路

方案选择

已调信号解调部分

方案一：采用STM32加FPGA的方式，利用数字正交解调电路进行计算解调。
方案二：采用FM,AM模拟解调系统，通过使用NE564FM解调电路解调FM已调信号， 通过采用KDL5511模块的电路进行AM信号解调，解调后通过滤波器滤波后得到原信号。
方案三：采用STM32H750VBT6单片机和全数字解调信号系统， 采用STM32进行数字滤波解调，采取差分解调的方法。
综合比较以上三个方案，方案一实现难度大，且需要FPGA成本高。方案三算法要求过高，对MCU占用过高，综上，我们计划使用方案二，即硬件解调的方式，方法简便稳定，且带宽较宽，完全可以满足题目基本要求。
我看到很多博客用的都是FPGA解调，这种方法我们之前没有接触过，所以果断放弃。数字解调其实我们也尝试了一整晚，没有一点收获，最后只能借助硬件电路来进行解调，由于要求的频率和带宽限制并不苛刻，还是能够完整实现的。

测量并显示$U_{AM}$的调幅度$m_a$

方案一：根据调幅度定义式得其计算公式为$m_a$=[(A-B)/(A+B)]。通过计算得到波形垂直方向上的最大幅度A和最小幅度B。
方案二：根据调幅度的定义，可以得计算公式为$m_a$=10^((A-6.02)/20)。通过FFT测量调制边带与载波之间的幅度差A(dB)。
计算测量波形垂直方向幅值对软件有更高的要求，而FFT测量调制边带和载波幅度差相对更容易，而且对其他要求的实现方案也有帮助。故这里选择方案二。

测量并显示$U_{FM}$的调幅度$m_f$和最大频偏|$\Delta$$f_m$|

方案一：测周法：$m_f$=T×(t2-t1)/4t1t2。采样得到调频波最疏处与最密处频率，进而得到t1，t2。采用TLV3501测量调频波频率，进而得到周期T。
方案二：零阶Bessel函数零值法。零阶Bessel函数J0(mf)在某些点值为零，即频谱图上所看到载频点的信号为零。这些点与mf之间有对应关系，可以通过查表求出调频度。
方案三：Bessel函数比值法：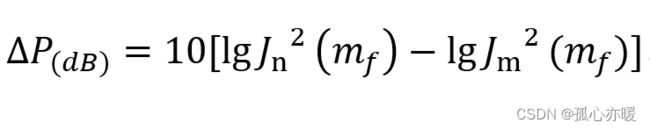

采用FFT测量调频信号频谱分量间的比值，通过查表可以得到调频度。
利用调频度和最大偏频之间的关系∆$f_m$=$m_f$×F ，即可求出最大偏频。
考虑调频信号频率太高，采样得到的各处频率不够精确，而且零值法对频谱图的精度要求太高，因此前两种方案舍弃。FFT可以满足测量需求，自行制表可以完成调频度测量。故选用方案三。

这里详细说一下调频度$m_f$的计算。

调频信号的表达式为u(t)=Ucos[${\omega }_0$t+$m_f$sin⁡(Ωt)]……(1)
其中${\omega }_0$为载波信号频率,Ω为调制频率,$m_f$为调频指数。
将公式（1）展开，其表达式为
u(t)=U{ $J_0$($m_f$ )cos${\omega }_0$t+$J_1$($m_f$)[cos(${\omega }_0$+Ω)t-cos(${\omega }_0$-Ω)t)+$J_2$($m_f$)[cos(${\omega }_0$+2Ω)t-cos(${\omega }_0$-2Ω)t] +$J_3$($m_f$)[cos(${\omega }_0$+3Ω)t-cos(${\omega }_0$-3Ω)t+⋯}

$J_n$($m_f$)为贝塞尔（Bessel）函数。
从上式可以看出，调频信号频谱包含很多边频分量，边频分量的幅度值由贝塞尔函数$J_n$($m_f$)决定，即取决于实际调制指数$m_f$。由此可以计算出调频指数$m_f$。

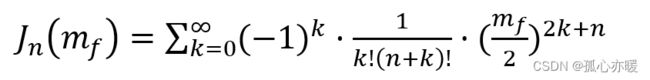
上式中，n为边带数，n=0是载频，n=1是第一边频，n=2是第二边频……;k=1、2、……;$m_f$为调频指数，
利用调频指数与调制频偏之间的关系，可以计算出最大频偏∆$f_m$: ∆$f_m$=$m_f$×F
在上式中，$m_f$是调频指数，F为调制频率。
对于$m_f$的计算，根据表达式（5）中的贝塞尔（Bessel）。查表可得出$m_f$。此法即贝塞尔（Bessel）函数比值法。

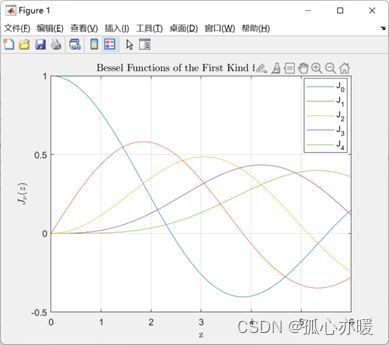
上图为Matlab绘制出$J_{0to4}$（mf）的曲线与$m_f$的关系。

rata1 = zeros(301,1);%J1与J0比值
rata2 = zeros(301,1);%J2与J0比值
rata3 = zeros(301,1);%J3与J0比值
rata4 = zeros(301,1);%J4与J0比值
mf = 0:0.02:6;
i = 1;
for z = 0:0.02:6
    rata1(i) = (besselj(1,z)/besselj(0,z))^2;
    rata2(i) = (besselj(2,z)/besselj(0,z))^2;
    rata3(i) = (besselj(3,z)/besselj(0,z))^2;
    rata4(i) = (besselj(4,z)/besselj(0,z))^2;
    i = i + 1;
end
rela_form = [mf',rata1,rata2,rata3,rata4];%各组比值和mf关系

最常用的比值计算是计算出${J_1}^2(m_f)$与${J_0}^2(m_f)$之间的比值与实际FFT测量出来的幅值进行查表比较，进而推算出mf的具体值。但是我们通过计算其比值，对比题目要求发现，当1<$m_f$<=6时，该结果并非一个单调函数，通过查表无法确定$m_f$的值，如下图所示：

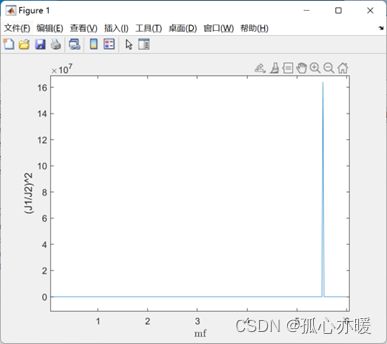
经过分析计算，我们决定采用$J_{1to4}(m_f)$与$J_0(m_f)$之间的平方比值，进行四维空间匹配，计算求欧氏距离。

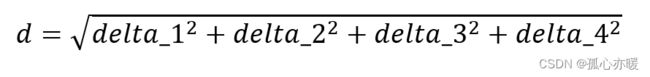
通过查阅已经计算得到的数值表，如下所示。
表1 1~4阶Bessel函数值与0阶Bessel函数值平方比关于$m_f$关系表（部分）

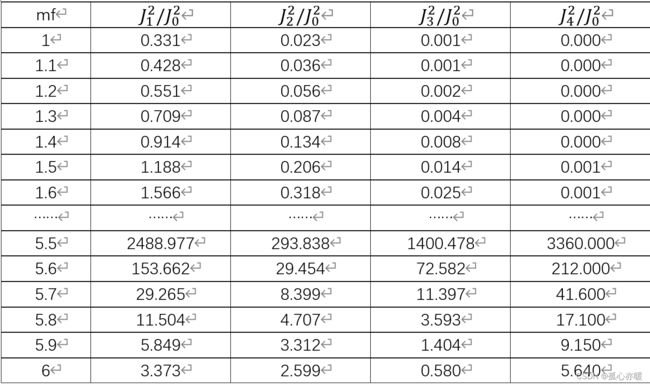
匹配最小欧氏距离值，我们可以得到$m_f$的精确值。

自主识别$U_m$的调制方式

采用FFT和“寻峰算法”得到谱线数量，通过比较谱线数量识别$u_m$的调制方式：若谱线数为1，则为未调制信号；若谱线数为3，则为调幅信号（AM）；若谱线数大于3，则为调频信号（FM）。

硬件电路设计

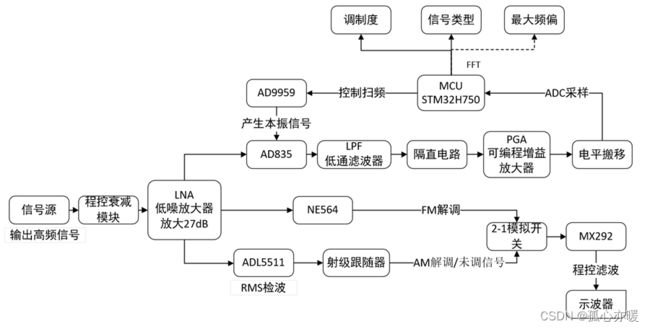
总体框架

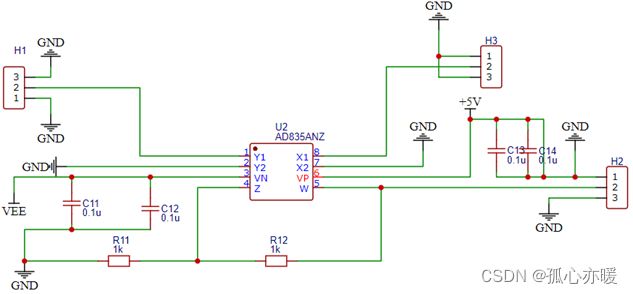
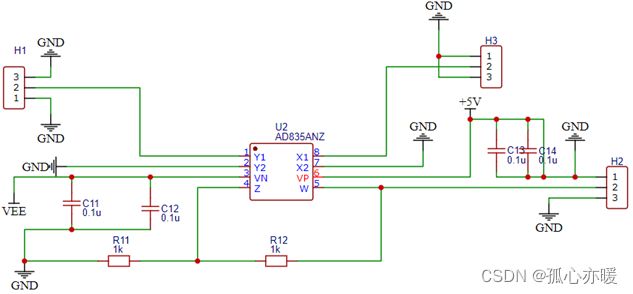
混频器电路

前级混频器使用AD835乘法混频电路，带宽为250M，符合题目要求，AD835为四象限乘法器，调制解调器，线性度较好，用于将FM，AM已调信号从高频域搬移至低频域。

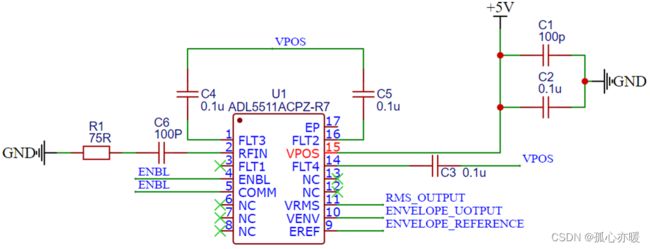
AM解调电路

AM解调使用基于ADL5511芯片的RMS检波器，该芯片的带宽可以达到6GHz，单电源5V供电，该电路可以直接检测出混频之前的AM信号，并将其解调，解调后通过±5V双电源供电的射极跟随器和隔直电路得到最终的解调信号。

FM解调电路

我们使用基于NE564的FM解调模块以及基于MAX291的程控滤波器对解调信号进行滤波，得到最终的FM信号。

软件设计

总体框架

用Matlab程序来完成理论计算。

该程序通过自己产生FM信号，处理产生信号得到$m_f$值，计算理论$m_f$值，比较作图。

clear all;
close all;
%% 生成mf以及各比值与mf的关系
rata1 = zeros(301,1);
rata2 = zeros(301,1);
rata3 = zeros(301,1);
rata4 = zeros(301,1);
rata5 = zeros(301,1);
rata6 = zeros(301,1);
i = 1;
for z = 0:0.02:6
    rata1(i) = (besselj(1,z)/besselj(0,z))^2;
    rata2(i) = (besselj(2,z)/besselj(0,z))^2;
    rata3(i) = (besselj(3,z)/besselj(0,z))^2;
    rata4(i) = (besselj(4,z)/besselj(0,z))^2;
    rata5(i) = (besselj(5,z)/besselj(0,z))^2;
    rata6(i) = (besselj(6,z)/besselj(0,z))^2;
    i = i + 1;
end
rela_form = [rata1,rata2,rata3,rata4,rata5,rata6];
tt=1:0.1:6;
length_1=size(tt);
mf_find_copare=zeros(2,length_1(2));
kk=1;
for mf=1:0.1:6
    %% 产生fm信号
    fmod = 10e3; % 调制信号频率(Hz)
    Amp = 1; % 调制信号幅度
    fc = 100e3; % 载波频率(Hz)
    Ac = 6; % 载波幅度
    kf = mf * 2 * pi * fmod / Amp
    diatf = kf * Amp
    B = 2 * (mf + 1) * fmod
    fs = 819200; % 采样率
    N = 4096; % 样点总数
    t = (0:N-1)'/fs; % 时间t
    %绘制时域波形
    m_t = Amp*sin(2*pi*fmod*t); % 调制信号
    phi_t = kf*cumsum(m_t)/fs; % 相位积分
    s_t = cos(2*pi*fc*t + phi_t); % 已调信号\

    %% 峰值提取
    s_t = awgn(s_t,15,'measured'); 
    FFT_Fm=abs(fft(s_t,4096));  
    Input_Amp=FFT_Fm;
    figure(2)
    subplot(2,1,1)
    plot(Input_Amp);
    subplot(2,1,2)
    plot(FFT_Fm);

    Amp1=zeros(2048,1);
    Amp2=Amp1;
    Amp3=Input_Amp;
    Amp_find_cnt=0;
    Amp_find_index=zeros(1,50);
    Wave_type=0;
    for i=1:2048
        if Input_Amp(i)<0.01*1000
            Amp1(i)=0.01*1000;
        else
            Amp1(i)=Input_Amp(i);
        end
    end
    Amp3(1)=0;Amp3(2)=0;
    for i=3:2048
        if Amp1(i)/Amp1(i-2)>5
            Amp2(i)=1;
        else
            Amp2(i)=0;
            Amp3(i)=0;
        end
    end
    Amp_find_cnt=0;
    for i=2:2047
        if Amp3(i)>=Amp3(i-1) && Amp3(i)>Amp3(i+1) 
            Amp_find_cnt=Amp_find_cnt+1;
            Amp_find_index(1,Amp_find_cnt)=i;
        end
    end
    Amp_find_cnt
    Amp_find_index(1,1:Amp_find_cnt)

    if Amp_find_cnt==1
        Wave_type=0;
    elseif Amp_find_cnt==3
        Wave_type=1;   
        Am_index=Amp3(1,Amp_find_index(2))/Amp3(1,Amp_find_index(1))%需要替换
    else
        Wave_type=2; 
        fc_cal=round(fc*N/fs);% fc*4096/819200
        for i=1:Amp_find_cnt
            if Amp_find_index(i)>= (fc_cal-2)&& Amp_find_index(i)<=(fc_cal+2)  % 70kHz中频
                Amp_find_index(i)
                J0=Amp3(Amp_find_index(i))^2
                J1_J0=Amp3(Amp_find_index(i-1))^2/J0;
                if i>2
                 J2_J0=Amp3(Amp_find_index(i-2))^2/J0;
                else
                 J2_J0=0;
                end            
                if i>3
                 J3_J0=Amp3(Amp_find_index(i-3))^2/J0;
                else
                 J3_J0=0;
                end
                if i>4
                    J4_J0=Amp3(Amp_find_index(i-4))^2/J0;
                else
                    J4_J0=0;
                end
                if i>5
                    J5_J0=Amp3(Amp_find_index(i-5))^2/J0;
                else
                    J5_J0=0;
                end
                if i>6
                    J6_J0=Amp3(Amp_find_index(i-6))^2/J0;
                else
                    J6_J0=0;
                end
                break;
            end
        end           
    end
%计算并寻找最短欧氏距离
    mindelta = 65535;
    i=1;
    length=size(rela_form);
    for i = 1:length(1)
         distence = (J1_J0-rela_form(i,1))^2+(J2_J0-rela_form(i,2))^2+(J3_J0-rela_form(i,3))^2+(J4_J0-rela_form(i,4))^2;
%        distence = abs(J1_J0-rela_form(i,1))+abs(J2_J0-rela_form(i,2))+abs(J3_J0-rela_form(i,3))+abs(J4_J0-rela_form(i,4))+abs(J5_J0-rela_form(i,5))+abs(J6_J0-rela_form(i,6));
        if distence <= mindelta
           mindelta = distence; 
           mf_find=(i-1)*0.02;
       end
    end
    mf_find_copare(1,kk)=mf;%mf理论情况
    mf_find_copare(2,kk)=mf_find;%mf计算结果
    mf
    mf_find
    kk=kk+1;
end
figure(3)
subplot(2,1,1)
plot(mf_find_copare(1,:),'--r')
hold on
plot(mf_find_copare(2,:),'--b')
%mf计算结果和理论误差
subplot(2,1,2)
plot(mf_find_copare(1,:)-mf_find_copare(2,:),'--k')

通过我们的程序可以看到误差情况，红线为理论结果，蓝线为计算结果。在$m_f$取3.0和4.3左右的时候，计算结果误差还是相对比较大的。这也算是我们这次的一点小瑕疵。

测评的时候老师偏偏把数值选到了这几个点，我们测试最精准的地方没有展示出来，反倒这些细节全部被老师抠出来了。不愧是经验丰富的老师啊！

关于单片机程序

我负责的主要是理论计算以及协助硬件电路搭建，软件这里我们组员完全按照matlab程序移植，设计寻峰算法以及液晶屏显示的工程。

我觉得移植matlab程序不算难事，相信各位读者能够很轻松按照这个思路完成整个信号调制度的计算、识别和显示。

写在最后的话

这个博客写了好久了，今晚终于静下心来完成了。不过我不是很满意，没有展示我们的keil工程代码，硬件电路也是含糊带过。重点全放在了$m_f$计算上了。未来还会慢慢完善的。我不太了解别的队伍是怎么计算这个问题的，我们当时花了很多功夫在计算这里。电路和程序反倒是我们基本功的展示。最后的结果不算完美，但这也是我们好久以来第一次认认真真去完成的一件事情，比赛四天睡了六个小时，每天都在焦急和忙碌之中，经历过各种失败，最后完成了这样一个不算完美的作品。如果本篇内容有不足之处，请大家多多包涵，提出建议，互相交流学习！