【金融量化分析】#期权相关定价方法与代码表达
期权主要使用的定价方法有偏微分方程法、鞅方法和数值方法。而数值方法又包括了二叉树方法、有限差分法和蒙特卡洛模拟方法。
想了解下不?
不想?滚
想,那得先知道 Black-Scholes 期权定价公式
Black-Scholes 期权定价公式(偏微分方程SDE)
简单推导期权定价模型:https://zhuanlan.zhihu.com/p/399851702
说人话就是:模型在推导过程中运用到了一个很重要的微分方程:
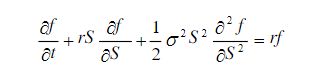
其中,式子中的 f 表示看涨期权价格,S表示期权基础资产的价格,r为连续复利的无风险收益率,σ为基础资产价格百分比变化(收益率)的波动率,t是时间变量。

Code:
function Call = blsprice(S,K,r,T,sigma)
% BS formula for European call pricing
d1 = (1./(sigma.*sqrt(T))).*( log(S/K) + (r+sigma.^2/2).*T);
d2 = d1 - sigma.*sqrt(T);
Z1 = normcdf(d1,0,1);
Z2 = normcdf(d2,0,1);
Call = Z1*S - Z2*K*exp(-r*T);
end
python代码实现
import numpy as np
from scipy.stats import norm
def call_BS(S,K,sigma,r,T):
'''用bs模型计算欧式看涨期权价格
S 期权基础资产价格
K 期权执行价格
sigma 基础资产价格百分比变化(收益率)的年化波动率
r 无风险收益率
T 期权合约剩余年限
'''
d1 = (np.log(S/K) + (r + pow(sigma,2)/2)*T) / (sigma*np.sqrt(T))
d2 = d1 - sigma*np.sqrt(T)
return S*norm.cdf(d1) - K*np.exp(-r*T)*norm.cdf(d2)
def put_BS(S,K,sigma,r,T):
'''用bs模型计算欧式看跌期权价格
S 期权基础资产价格
K 期权执行价格
sigma 基础资产价格百分比变化(收益率)的年化波动率
r 无风险收益率
T 期权合约剩余年限
'''
d1 = (np.log(S/K) + (r + pow(sigma,2)/2)*T) / (sigma*np.sqrt(T))
d2 = d1 - sigma*np.sqrt(T)
return K*np.exp(-r*T)*norm.cdf(-d2) - S*norm.cdf(-d1)
B-S的应用:隐含波动率的计算
https://blog.csdn.net/hzk427/article/details/104501847
call put parity 看跌-看涨平价关系式(待补充)
具有相同执行价格与期限的欧式看跌期权、看涨期权在价格上有一个重要关系式。上面put的价格也由此推出
两个投资组合的讨论(无套利)
首先,考虑以下两个投资组合在期权合约到期时的盈亏情况。A投资组合:一份欧式看涨期权和一份在T时刻到期的本金为K的零息债券;B投资组合:一份欧式看跌期权和一份基础资产。这里需要假设看涨期权与看跌期权具有相同的执行价格K与相同的合约期限T。
对于A投资组合而言,零息债券在期权合约到期日(T时刻)的价值显然是等于K,而对于看涨期权则分两种情形讨论。
情形1:如果在T时刻,基础资产价格St>K,A投资组合中的欧式看涨期权将被执行,此时,A投资组合的价值是(St-K)+K=St;
情形2:如果在T时刻,基础资产价格St 对于B投资组合而言,也分两种情形讨论。 情形1:如果在T时刻,基础资产价格St>K,此时,B投资组合中的欧式看跌期权没有价值,此时,B投资组合价值为St,也就是仅剩下基础资产的价值; 情形2:如果在T时刻,基础资产价格St 由于A投资组合与B投资组合中的期权均为欧式期权,在期权到期之前均不能行使,既然两个投资组合在T时刻均有相同的收益,在期权合约的存续期内也应该有相同的价值。否则,就会出现无风险套利机会,套利者可以买入价格低的投资组合,与此同时卖空价格高的投资组合进行无风险的套利,无风险套利收益就是等于两个组合价值的差额。 公式如下: 通常被用来判断期权价格是否合理 Python代码实现 假设当前股票价格为20元股,期权的执行价格为18元/股,无风险收益率为每年5%,3个月的欧式看涨期权价格对外报价是2.3元,3个月的欧式看跌期权对外报价是0.3元,期权价格是否合理? 看涨期权被低估,看跌期权则被高估,因此可以通过持有看涨期权的多头头寸并买入零息债券(相当于买入A投资组合),同时持有看跌期权的空头头寸并卖空基础资产(相当于卖空B投资组合),从而实现无风险套利。 https://zhuanlan.zhihu.com/p/95538708 蒙特卡洛方法的理论基础是概率论与数理统计,其实质 是通过模拟标的资产价格路径预测期权的平均回报并得到 期权价格估计值。蒙特卡洛方法的最大优势是误差收敛率不 依赖于问题的维数,从而非常适宜为高维期权定价。 说人话:就TM4一种统计学的方法、模拟方法,通过大量随机样本模拟问题,从而获得所要计算的值。 https://blog.csdn.net/baidu_41327283/article/details/99289216 是不是很迷糊?接着看 就是有句话当讲不当讲都要讲:所有金融衍生品的价值都等于每一个时期预期获益的贴现后的现值 B-S 虽好,但是不同偏微分方程的菜鸡太多,而且不太适用于美式期权的定价 https://zhuanlan.zhihu.com/p/330957457 代码实现 美式看涨期权 相比欧式期权,美式期权需要先计算提前行权的收益判断是否提前行权。提前行权的收益为本节点上股票的预期价格减执行价格。如果收益大于期权价值,说明提前行权获利更多,因此会提前行权;反之则不会。
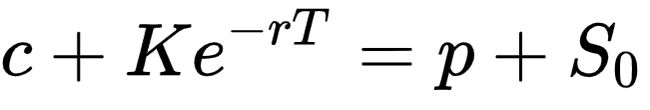
看涨期权 + 零息债券价格 = 看跌期权 + 基础资产价格 def call_parity(p,S,K,r,T):
'''通过平价关系式用看跌期权价格计算欧式看涨期权价格。
p:欧式看跌期权价格
S:期权基础资产价格
K:执行价格
r:无风险收益率
T:合约剩余期限
'''
return p + S - K * np.exp(-r * T)
def put_parity(c,S,K,r,T):
'''通过平价关系式,用看涨期权价格计算欧式看跌期权价格。
c:欧式看涨期权价格
S:期权基础资产价格
K:执行价格
r:无风险收益率
T:合约剩余期限
'''
return c + K * np.exp(-r * T) - S
举个例子
call_parity(p=0.3, S=20, K=18, r=0.05, T=0.25)
==>2.523599591110134
put_parity(c=2.3, S=20, K=18, r=0.05, T=0.25)
==>0.07640040888986732
Martingale 定价(待补充)
Monte Carlo 模拟是个啥
三门问题的应用
Monte Carlo method 期权定价
#蒙特卡洛模拟看涨期权价格
def call_MonteCarlo(S,K,T,r,sigma,n):
z = standard_normal(n) # 从标准正态分布中抽取一个样本
St = S*np.exp((r-0.5*sigma**2)*T+sigma*z*np.sqrt(T))
c = sum(np.maximum(0,St-K))*(np.exp(-r*T))/n
return c
#蒙特卡洛模拟看跌期权价格
def put_MonteCarlo(S,K,T,r,sigma,n):
z = standard_normal(n)
St = S*np.exp((r-0.5*sigma**2)*T+sigma*z*np.sqrt(T))
p = sum(np.maximum(0,K-St))*(np.exp(-r*T))/n
return p
c = call_MonteCarlo(5.29,6,0.5,0.04,0.24,5000)
p = put_MonteCarlo(5.29,6,0.5,0.04,0.24,5000)
print('蒙特卡洛模拟看涨期权价格为{:.4f},看跌期权价格为{:.4f}'.format(c,p))

那么第一步标的资产的价格路径如何模拟?

第二步中的期权到期汇报贴现是啥?自己去搜。。。

so,

二叉树模型(CRR Tree method )
这啥
而蒙特卡洛模拟在处理提前行权(美式期权)问题时表现出不足,这时就可以使用二叉树法求解import numpy as np
# 二叉树模型对欧式看涨期权定价
def binarytree_ecall(S, K, r, sigma, t, N):
'''S:标的资产价格;K:期权的执行价格;r:年化无风险利率(找到shibor加小数点);
sigma:标的资产收益率的标准差;t:年化的时间长度;N:二叉树的步长'''
deltaT = t / N
u = np.exp(sigma * np.sqrt(deltaT))
# 根据风险中性定价公式,求S方差,即可推导
d = 1 / u
P = (np.exp(r * deltaT) - d) / (u - d)
# 风险中性测度
prices = np.zeros(N + 1)
# 股票价格向量用0填充
calls = np.zeros(N + 1)
# 期权价格向量用0填充
for i in range(0, N + 1):
prices[i] = S * (u**i) * (d**(N - i))
# 一次计算第1、2……个价格dddd,uddd,udd,uud,uuu
calls[i] = np.maximum(prices[i] - K, 0)
# 然后计算对应的看涨期权价格
# 这样就得到了最后一层二叉树的股票价格和期权价格
for i in range(N, 0, -1):
# 二叉树叶节点往内部节点遍历
for j in range(0, i):
calls[j] = (
P * calls[j + 1] +
(1 - P) * calls[j]) * np.exp(-r * deltaT)
# 得到前一层的价格,此时已经是N个期权价格
# 下一次i迭代将变成N-1个期权价格,总共迭代N次
# 只剩下1个价格。
return calls[0]
c = binarytree_ecall(
S=2.265, K=2.05, r=0.019680, sigma=0.239174492, t=0.46, N=250)
print('50ETF欧式看涨期权的价格为', round(c, 100))
print('real open price: 0.29')
#二叉树法为美式看涨期权定价
def binarytree_ameripcall(S,K,r,sigma,t,steps):
'''
S: 标的资产初始价格;
K: 期权的执行价格;
r: 年化无风险利率;
sigma: 标的资产连续复利收益率的标准差;
t:以年表示的时间长度;
steps:二叉树的步长。
'''
u = np.exp(sigma*np.sqrt(t/steps))#时间间隔为△t=t/steps
d = 1/u
P = (np.exp(r*t/steps)-d)/(u-d)
prices = np.zeros(steps+1)
c_values = np.zeros(steps+1)
prices[0] = S*d**steps#生成最后一列的股票价格空数组
c_values[0] = np.maximum(prices[0]-K,0)#生成最后一列的期权价值空数组
for i in range(1,steps+1):
prices[i] = prices[i-1]*(u**2)#计算最后一列的股票价格
c_values[i] = np.maximum(prices[i]-K,0)#计算最后一列的期权价值
for j in range(steps,0,-1):#逐个节点往前计算
for i in range(0,j):
prices[i] = prices[i+1]*d#判断是否提前行权
c_values[i] = np.maximum((P*c_values[i+1]+(1-P)*c_values[i])*np.exp(-r*t/steps),prices[i]-K)
return c_values[0]
A2 = binarytree_ameripcall(S=810,K=800,r=0.05,sigma=0.2,t=0.5,steps=2)
print('二叉树法为美式看涨期权定价:',round(A2,2))






