作业1-PM2.5预测（李宏毅机器学习）

项目描述

• 本次作业的资料是从行政院环境环保署空气品质监测网所下载的观测资料。
• 希望大家能在本作业实现 linear regression 预测出 PM2.5 的数值。

数据集介绍

• 本次作业使用丰原站的观测记录，分成 train set 跟 test set，train set 是丰原站每个月的前 20 天所有资料。test set 则是从丰原站剩下的资料中取样出来。
• train.csv: 每个月前 20 天的完整资料。
• test.csv : 从剩下的资料当中取样出连续的 10 小时为一笔，前九小时的所有观测数据当作 feature，第十小时的 PM2.5 当作 answer。一共取出 240 笔不重複的 test data，请根据 feature 预测这 240 笔的 PM2.5。
• Data 含有 18 项观测数据 AMB_TEMP, CH4, CO, NHMC, NO, NO2, NOx, O3, PM10, PM2.5, RAINFALL, RH, SO2, THC, WD_HR, WIND_DIREC, WIND_SPEED, WS_HR。

项目要求

• 请手动实现 linear regression，方法限使用 gradient descent。
• 禁止使用 numpy.linalg.lstsq

环境配置/安装

!pip install --upgrade pandas

import numpy as np
import pandas as pd

导入训练集

data = pd.read_csv('work/hw1_data/train.csv', encoding = 'big5')  # 繁体字编码使用的是big5

预处理

取需要的数值部分，将 ‘RAINFALL’ 栏位全部补 0。

1. 取需要的部分时候会使用到pandas中DataFrame的iloc[]来进行选择，其中前面为行后面为类；
2. 对于补零，是因为数据中有缺示，为可以正常进行运算可以使用data[data == 'NR'] = 0对缺示值补零。

data = data.iloc[:,3:]
data[data=='NR'] = 0
raw_data = data.to_numpy()
raw_data.shape

(4320, 24)

因为原数据尺寸为[18*20*12,24]，这不符合题目要求的input格式，故需要进行相应的调整。

month_data = {}
for m in range(12):
    temp = np.empty([18,480])  
    for d in range(20):
        temp[:,d * 24 : (d + 1) * 24] = raw_data[18 * (20 * m + d) : 18 * (20 * m + d + 1), :]
    month_data[m] = temp

根据提示创建样本集和相应的标签

x = np.empty([12 * 471, 18 * 9], dtype = float)
y = np.empty([12 * 471, 1], dtype = float)

for m in range(12):
    for d in range(20):
        for h in range(24):
            # 当遍历到每月最后一天时会有不足形成一个样本的情况
            if d == 19 and h > 14:
                continue
            x[m * 471 + d * 24 + h, :] = month_data[m][:,d * 24 + h : d * 24 + h + 9].reshape(1, -1)
            y[m * 471 + d * 24 + h, 0] = month_data[m][9, d * 24 + h + 9]
print(x.shape)
print(y.shape)

(5652, 162)
(5652, 1)

获得原始input之后，可以使用feature scaling处理数据，从而优化训练效果。

产生训练时需要的训练集和验证集：

import math
x_train_set = x[: math.floor(len(x) * 0.8), :]
y_train_set = y[: math.floor(len(y) * 0.8), :]
x_validation = x[math.floor(len(x) * 0.8): , :]
y_validation = y[math.floor(len(y) * 0.8): , :]

训练

训练方法这里使用课程中刚刚讲到的线性回归，整个步骤可以概括为：

1. 初始化weights、input；
2. 计算Loss Function（用于检测模型是否有效）、gradient（用于weight的更新),重复步骤2直至满足停止条件。

关于其中learning rate的选择，在前面视频中李宏毅老师示范了AdaGrad的代码，作为AdaGrad的进阶算法Adam在Gradient Descent上的表现更加稳定，所以想手写简易的Adam算法用于learning rate的确定。

下图为论文中的Adam算法伪代码：

和AdaGrad不同的一个是分母不再是简单的偏导平方的累加,而是由一个小于1系数控制的累加，这个过程中前面的结果会随着迭代次数增加慢慢失去影响；另一个是在分子上增加了Momentum策略来增加跳出local minima的可能。

dim = 18 * 9 + 1
iter_time = 10000
# 初始化模型参数和input
w = np.zeros([dim, 1])
Input = np.concatenate((np.ones([x_train_set.shape[0], 1]), x_train_set), axis = 1).astype(float)

# adam算法初始化
alpha = 0.001
beta1 = 0.9
beta2 = 0.999
eps = 0.0000000001
m = np.zeros([dim,1])
v = np.zeros([dim,1])

for t in range(iter_time):
    loss = np.sqrt(np.sum(np.power(np.dot(Input,w) - y_train_set,2)))
    if not (t % 2000):
        print(f'{t}:{loss}')
    gradient = 2 * np.dot(Input.transpose(), np.dot(Input, w) - y_train_set)
    m = beta1 * m + ( 1 - beta1) * gradient
    v = v * beta2 + ( 1 - beta2) * gradient ** 2
    w = w - alpha * (m / (1 - beta1)) / ( np.sqrt( v / (1 - beta2)) + eps)
np.save('work/weight.npy', w)

0:1831.5460682166856
2000:441.15547337011577
4000:401.3307088430447
6000:387.7767101218769
8000:385.808532008417

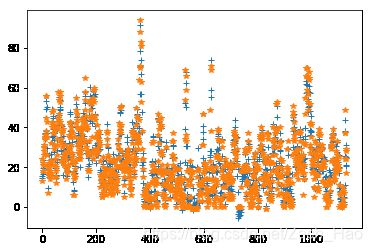
通过训练集进行训练后可以使用从样本集划分的验证集来检验训练模型的好坏，因为PM2.5的预测是对于值的预测，通过运算检测错误率并不能直观的说明结果的好坏，所以我在这里使用图形的方式将预测结果和标签画出来，因此可以直观的看到模型的效果：

from matplotlib import pyplot as plt 
import matplotlib

x_axis = np.arange(y_validation.shape[0])
x_validation_input = np.concatenate((np.ones([x_validation.shape[0], 1]), x_validation), axis = 1).astype(float)
y_axis = np.dot(x_validation_input,w)

plt.plot(x_axis,y_axis,'+')
plt.plot(x_axis,y_validation,'*')
plt.show()

从上面结果可以看到结果并不是很理想，可能是因为输入和PM2.5之间的关系不是简单的线性关系，所以如果要改进可能需要更换维度更高的模型进行训练；
也可能是因为我在数据处理的时候没有使用featrue scaling，在做的时候犯傻了，想假如归一化了怎么能够得到最后的PM2.5预测结果，后来还理直气壮地问助教，这才意识到标签（output）不归一化……

预测

利用上面训练的模型对于test.csv中数据进行预测，并且生成预测结果至submit.csv中。

# 数据导入
testdata = pd.read_csv('work/hw1_data/test.csv',  encoding = 'big5')

test_data = testdata.iloc[:, 2:]
test_data[test_data == 'NR'] = 0
test = test_data.to_numpy()

x_test = np.empty([239, 18*9], dtype = float)
for i in range(239):
    x_test[i, :] = test[18 * i: 18* (i + 1), :].reshape(1, -1)
x_test = np.concatenate((np.ones([x_test.shape[0], 1]), x_test), axis = 1).astype(float)

x_test.shape

# 模型导入
w = np.load('work/weight.npy')

res = np.dot(x_test, w)

import csv
with open('work/submit.csv', mode='w', newline='') as submit_file:
    csv_writer = csv.writer(submit_file)
    header = ['id', 'value']
    print(header)
    csv_writer.writerow(header)
    for i in range(239):
        row = ['id_' + str(i), res[i][0]]
terow(header)
    for i in range(239):
        row = ['id_' + str(i), res[i][0]]
        csv_writer.writerow(row)

['id', 'value']